
2012_phys_lp
.pdf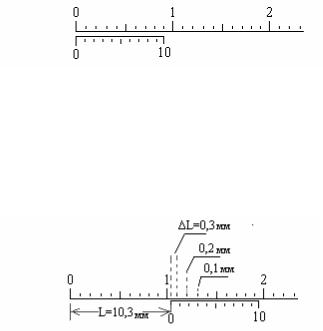
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
21
Линейный нониус состоит из двух перемещающихся одна относительно другой линеек с нанесенными на них шкалами: основной масштабной шкалой и дополнительной шкалой нониуса.
Разберем общие принципы устройства нониусов, которые можно применять и к угловым нониусам.
Одно деление шкалы нониуса меньше, чем одно или несколько (например k ) делений основного масштаба на 1/ n часть деления основного масштаба ( n
– целое число). Наиболее часто используются нониусы, содержащие 10 и 20 делений.
Точностью нониуса называют величину y / n , равную отношению цены наименьшего деления основного масштаба y к числу делений нониуса n . Цену делений основного масштаба либо указывают на самом приборе, либо легко определяют по цифрам, нанесенным на шкале основного масштаба.
Для десятичного нониуса n = 10 , y = 1 мм, k = 2 , вся длина шкалы нониу-
са, т.е. 10 его делений будут равны:
y × (k × n -1) = 1× (10 × 2 -1) = 19 мм.
Десятичный нониус дает возможность измерять длину с точностью до 0,1 деления основного масштаба, он является самым простым. Шкала нониуса разбита на 10 равных делений (рис.2.1).
Если нулевой штрих нониуса сов- |
|
|
падает с каким-либо штрихом масшта- |
|
|
ба, то совпадает и десятый штрих, но |
Рис. 2.1 |
|
остальные штрихи нониуса не совпада- |
||
|
ют со штрихами масштаба (см. рис.2.1). Если же нулевой штрих не совпадает с масштабным, то найдется такой штрих шкалы нониуса, который совпадает с каким-либо штрихом основного масштаба (или они будут находиться на наи-
меньшем расстоянии, чем другие). |
|
В случае, изображенном на рис.2.2, |
|
точно с масштабным штрихом совпада- |
|
ет третий штрих нониуса. Второй |
|
штрих слева будет отстоять от мас- |
|
штабного штриха на 0,1 мм. Следую- |
Рис. 2.2 |
щий штрих не будет совпадать с мас- |
|
штабным на 0,2 мм, а нулевой штрих |
|
нониуса не совпадает с масштабным уже на 0,3 мм. Следовательно, для нахождения десятых долей при помощи десятичного нониуса нужно номер “ совпа-
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
22
дающего” деления нониуса умножить на 0,1. Общая длина измеряемого отрезка на рис.2.2 будет равна 10,3 мм.
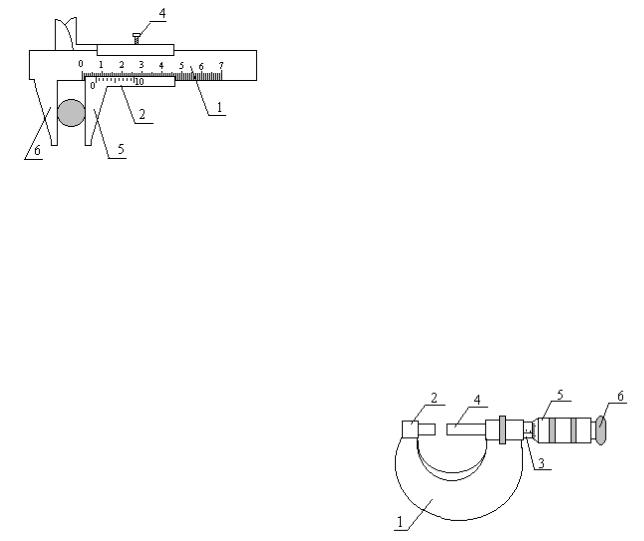
Штангенциркуль (рис. 2.3) состоит из линейки 1 (штанги) с миллиметровыми делениями и подвижной рамки 2 с нониусом и закрепляющим винтом 4. На штанге и рамке имеются ножки 5 и 6, которые с внутренней стороны имеют плоские поверхности.
При сомкнутых вместе ножках штангенциркуля отсчет по нониусу равен нулю. Измеряемый предмет помещается между ножками (при этом нужно избегать перекоса). При измерении штангенциркуль берут в правую руку, а измеряемый предмет придерживают левой рукой.
Часто штангенциркули снабжают еще одной рамкой с закрепляющим и микрометрическим винтами. Для более точного отсчета измерения можно производить следующим образом. Измеряемый предмет
слегка зажимают ножками. Затем закрепляют винт 4 и производят отсчет по нониусу.
Для измерения внутренних размеров пользуются специально отшлифованными концами ножек 5 и 6, толщина которых известна и нанесена на них (в мм). В некоторых конструкциях штангенциркулей имеется соединенная с рамкой рейка, используемая для измерения глубины отверстий.
Микрометр (рис. 2.4) состоит из скобы |
|
1 с упором 2 и трубкой (стеблем) 3. В труб- |
|
ке имеется внутренняя резьба, в которую |
|
ввинчен микрометрический винт 4 с закреп- |
|
ленным на нем барабаном 5. На конце бара- |
|
бана имеется фрикционная головка (тре- |
|
щотка) 6. |
|
Действие микрометра основано на |
Рис. 2.4 |
свойстве винта совершать при повороте его |
|
поступательное перемещение, пропорциональное углу поворота. При измерении предмет зажимают между пяткой и микрометрическим винтом. Для вращения барабана при этом пользуются фрикционной головкой. При определенной степени нажатия головка начинает проскальзывать и выдавать характерный треск. Этим приемом микрометрический винт предохраняется от порчи.
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
23
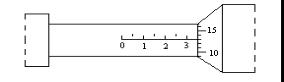
На трубке 3 нанесены деления основной шкалы. Барабан 5 при вращении винта перемещается вдоль трубки. На барабане нанесена добавочная шкала. В микрометрах МК-25 шаг микрометрического винта 0,5 мм (шаг – это смещение барабана вдоль основной шкалы за один полный оборот барабана). При этом половинные деления, чтобы не загромождать шкалу, располагаются над прямой линией основной шкалы (рис. 2.5). Шкала барабана разбита на 50 делений. Цена деления барабана равна 0,01 мм (т.е. поворот барабана на одно деление соответствует продольному перемещению винта на 0,01 мм).
Следует учесть, что последующее деле- |
|
ние основной шкалы начинает показываться |
|
из-под края барабана несколько раньше мо- |
Рис. 2.5 |
|
|
мента прохождения нулевого деления шкалы |
|
барабана мимо продольной черты основной шкалы. Поэтому в случае, когда отсчет по барабану немного не доходит до 50, начавшее появляться деление основной шкалы не следует принимать во внимание.
Перед началом работы с микрометром следует убедиться в его исправности. Перед измерением следует также проверить нулевую точку микрометра. Если при соприкосновении винта 4 с упором 2 против нулевого деления шкалы стоит ненулевое деление барабана, то следует учитывать эту систематическую ошибку прибора. Если отклонение велико, то микрометр требует регулировки.
В лабораторной работе применяются электронные весы. Принцип действия весов основан на преобразовании силы тяжести взвешиваемого груза в аналоговый электрический сигнал, преобразовании его в цифровую форму и последующей цифровой обработке на однокристальной ЭВМ с выдачей результата на цифровой индикатор.
Весы состоят из основания, пластмассового кожуха и грузоприемной чашки. В верхней части кожуха весов имеется кнопка включения питания [I/0] и кнопка [СБ], предназначенная для обнуления показаний индикатора при отсутствии груза.
Порядок выполнения работы
1.Получите у преподавателя образец.
2.Измерьте линейные размеры образца (высоту, ширину, длину, диаметры). Каждое измерение произведите 5 раз. Данные запишите в таблицу 2.1.
3.Произведите взвешивание образца на весах не менее 5 раз, результаты запишите в таблицу 2.1.
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
24
Обработка результатов измерений
1.Определите среднее значение измеренных величин (здесь x – это ширина, высота, длина, радиус или масса образца):
|
|
|
n |
|
||||
|
|
∑ xi |
|
|||||
x |
= |
i=1 |
. |
|
|
(2.7) |
||
|
|
|
||||||
ср. |
|
|
|
n |
|
|||
|
|
|
|
|
||||
2. Определите абсолютную погрешность каждого измерения: |
|
|||||||
xi = |
|
xср − xi |
|
. |
(2.8) |
|||
|
|
|||||||
3.Определите абсолютную случайную погрешность результата нескольких измерений (доверительный интервал) по формуле Стьюдента:
|
|
|
|
n |
|
)2 |
|
|
|
|
|
|
∑ ( |
x |
. |
(2.9) |
|
x |
=t |
|
× |
i =1 |
i |
|
||
P,n |
|
|
||||||
|
|
|
||||||
сл. |
|
|
n(n-1) |
|
||||
|
|
|
|
|
||||
Значение коэффициента Стьюдента tP,n возьмите из таблицы в приложении.
4.Определите абсолютную приборную погрешность xïð . , равную половине цены деления прибора.
5.Вычислите окончательное значение абсолютной погрешности
Dx = (Dx |
)2 +(Dx |
пр. |
)2 . |
(2.10) |
сл. |
|
|
|
6.Округлите полученную величину абсолютной погрешности.
7.Определите относительную погрешность результатов
E ( x) = x ×100% . |
(2.11) |
x |
|
8.Результат измерения линейных размеров представьте в виде: x = xср ± x . Не забудьте указать размерности величин. Укажите также относительную погрешность.
9.Вычислите среднее значение плотности образца ρср. по одной из формул
(2.4), используя средние значения массы и линейных параметров образца.
10.Получите формулу для расчета относительной погрешности плотности образца. В качестве примера приведён вывод формулы для погрешности плотности полого цилиндра.
|
|
|
¶ρ |
|
|
2 |
|
¶ρ |
|
|
2 |
|
¶ρ |
|
|
2 |
¶ρ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Dρ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Dm |
+ |
|
Dh |
+ |
|
Dd1 |
|
+ |
|
|
|
|
Dd2 . |
|
|
|
|
|
|
(2.12) |
||||||||||
|
|
¶m |
¶h |
¶d1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶d2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
11. После расчёта производных (см. формулу (2.4б)) получим: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
4 × Dm |
|
|
|
2 |
|
|
4m × Dh |
|
2 |
|
|
4 × 2md × Dd |
|
|
2 |
|
4 × 2md |
2 |
× Dd |
2 |
2 |
|
|||||||||||
Dρ = |
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
- |
|
|
1 |
|
1 |
|
|
+ |
|
|
|
|
|
|
(2.13) |
||||||
π h(d 2 - d |
2 ) |
|
π h |
2 (d |
|
- d |
2 ) |
π h(d 2 |
- d |
|
|
π h(d |
|
- d |
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 )2 |
|
|
2 |
2 ) |
2 |
|
|||||||||||||||||||
|
|
1 |
2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
25
12. |
Вычислите |
абсолютную ρ и относительную Е(ρ ) = |
|
ρ |
погрешности |
|
ρ |
||||
|
|
|
|
|
|
|
плотности образца. |
|
|
|
|
13. |
Окончательный результат представьте в виде: ρ = ρср. ± |
ρ , округлив вели- |
|||
|
чины ρср. и |
ρ в соответствии с правилами округления. |
|
|
|
14.Сделайте выводы. Представьте в выводах полученные значения плотности, абсолютной и относительной погрешности результата.
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.1 |
||
|
|
|
Образец (цилиндр, параллелепипед или т.п.) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
а, |
аi, |
b, |
bi, |
h, |
hi, |
m, |
|
mi, |
ρ, |
|
ρ, |
Е(ρ), |
п/п |
м |
м |
м |
м |
м |
м |
кг |
|
кг |
кг/м3 |
кг/м3 |
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Измерительный прибор (линейка; штангенциркуль; |
|
|
|
|
|
|
|
|||||
|
|
|
микрометр); |
|
|
|
|
|
|
|
|
|
|
|
параметр образца (радиус, высота или т.п.) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аср.= |
асл.= |
bср.= |
bсл.= |
hср.= |
hсл.= |
mср.= |
mсл.= |
|
|
|
|
|
|
|
апр.= |
|
bпр.= |
|
hпр.= |
|
|
mпр.= |
|
|
|
|
|
|
а= |
|
b= |
|
h= |
|
|
m= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Что значит измерить физическую величину?
2.Какие бывают измерения?
3.Дайте определения цены деления прибора и его чувствительности.
4.Что такое нониус? Чему равна цена деления его?
5.Измерьте штангенциркулем (микрометром) линейный размер предложенного образца.
6.Что такое класс точности прибора?
7.Что берут за величину погрешности, если не указывается класс точности прибора?
8.Как можно увеличить точность измерения?
9.Как определяется абсолютная погрешность при прямых однократных и многократных измерениях?
10.Как вычисляется ошибка при косвенных измерениях?
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
26
11.Получите формулы для вычисления абсолютной и относительной погрешности плотности сплошного цилиндра и прямоугольного параллелепипеда, исходя из (2.4) и (2.4а), аналогичные (2.13).
Используемая литература
[8]; [9].
Лабораторная работа 1-03 Изучение характеристик механического гироскопа
Цель работы: изучение особенностей динамики быстро вращающегося твердого тела и измерение его основных параметров: момента импульса, момента инерции и скорости прецессии.
Теоретическое введение
Гироскопом называется массивное тело, быстро вращающееся вокруг своей оси симметрии. При вращении вокруг этой оси момент импульса гироскопа совпадает по направлению с осью вращения. Такое вращение устойчиво, и ось вращения гироскопа сохраняет неизменным свое направление при любом повороте или передвижении прибора.
Гироскоп – слово греческого происхождения (гирос – вращение; скопейн – видеть, наблюдать). Это название прибору дал французский физик Леон Фуко.
В общем случае под гироскопом понимают твердое тело любой формы, которое совершает вращательное движение. Земной шар, делающий один оборот за сутки, подчиняется гироскопическим законам точно так же, как технические гироскопы, вращающиеся с большей угловой скоростью относительно главной оси по сравнению со скоростями вокруг любых других осей. Гироскопами заполнен микромир: орбитальное движение и спины электронов, спин атомных ядер являются неисчерпаемой кладовой гироскопии в недрах микромира.
Гироскопические приборы и устройства находят широкое применение в различных отраслях техники. Элементарное представление об особенностях поведения гироскопа дает обыкновенный волчок с его поразительно малой восприимчивостью к воздействию внешних сил и моментов. Гироскопы чаще всего применяются для ориентации, для определения тех или иных направлений. Также гироскопы используются в горном деле для определения кривизны буро-
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
27
вых скважин, для записи неправильностей железнодорожного пути. В авиации гироскопические приборы применяются в качестве основных чувствительных элементов (определение направления вертикали и курса), а также для измерения угловой скорости самолета.
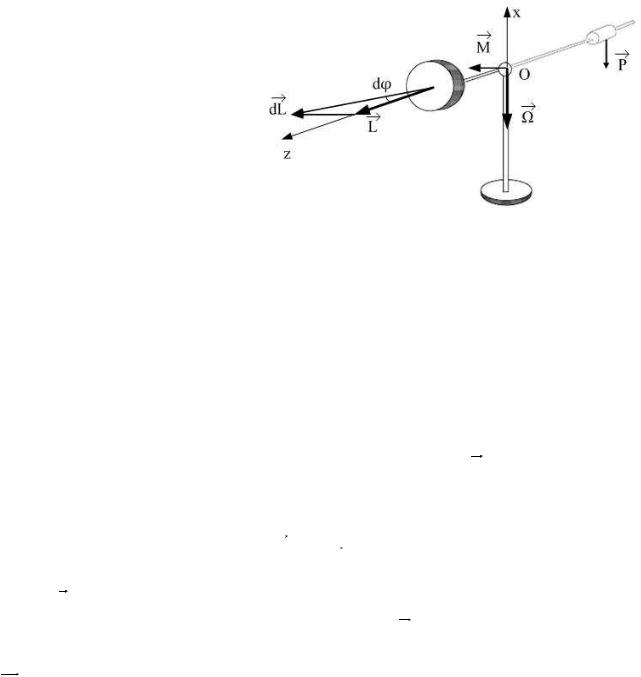
Гироскоп в кардановом подвесе имеет три степени свободы. Если центр масс гироскопа совпадает с точкой О – точкой опоры гироскопа, то гироскоп называется уравновешенным.
В простейшем варианте гироскоп выполняется в виде массивного диска, насаженного на вал (рис. 3.1).
Для изменения направления оси гироскопа относительно неподвижной системы координат необходимо, чтобы на него действовал момент внешних сил. В таком случае наблюдается явление, называемое гироскопическим эффектом: под действием сил, которые, казалось бы, должны были вызвать
поворот оси гироскопа в той плоскости, в которой лежат эти силы, в действительности ось гироскопа поворачивается вокруг оси, перпендикулярной к указанной плоскости. Такое вращение называют прецессией.
Гироскопический эффект основан на законах вращательного движения твердых тел. Пусть имеется уравновешенный гироскоп (рис. 3.1), который может вращаться вокруг осей OZ и OX. Приведем его во вращение вокруг собственной оси OZ. Тогда его момент импульса
|
|
L = I ×ω , |
(3.1) |
где I – момент инерции гироскопа относительно его оси; |
ω – угловая скорость |
||
собственного вращения гироскопа. |
|
||
При отсутствии внешнего вращающегося момента |
|
||
|
d L |
= 0 , L = const , |
(3.2) |
|
|
||
|
dt |
|
|
вектор L сохраняет свою величину и направление.
Подвесим на конец осевого стержня груз P . Он будет действовать на стержень, жестко связанный с осью гироскопа. Возникнет момент этой силы
M , лежащий в горизонтальной плоскости. Изменение момента импульса гироскопа под действием этого момента силы равно
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
28
|
|
|
|
|
|
|
× dt . |
|
|||||||||
|
|
|
dL = M |
(3.3) |
|||||||||||||
За время Dt |
момент импульса гироскопа получит приращение |
||||||||||||||||
|
|
|
DL = M × Dt , |
(3.4) |
|||||||||||||
которое имеет такое же направление, как и M , то есть вектор |
DL перпенди- |
||||||||||||||||
кулярен вектору |
L (рис.3.1). Так как момент внешних сил мал, вектор L по- |
||||||||||||||||
стоянен по модулю и изменяется лишь по направлению. Сила |
P , не изменяя |
||||||||||||||||
величины вектора |
L , заставляет его конец описывать окружность в горизон- |
||||||||||||||||
тальной плоскости. Таким образом, |
гироскопический эффект |
непосредствен- |
|||||||||||||||
но следует из основного уравнения вращательного движения. |
|
||||||||||||||||
Найдём Ω – |
угловую скорость прецессии, то есть дополнительного вра- |
||||||||||||||||
щения оси гироскопа под действием постоянного момента сил M . |
|||||||||||||||||
За время dt |
вектор L в горизонтальной плоскости повернется на угол dϕ , |
||||||||||||||||
причем, как следует из (3.3) и рис. 3.1, |
|
|
|
|
|
|
|
||||||||||
|
|
|
dϕ = |
dL |
= |
M × dt |
. |
(3.5) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
L |
|
|
L |
|
||||||
Таким образом, угловая скорость B вращения вектора L (угловая скорость |
|||||||||||||||||
прецессии) равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
dϕ |
= |
M × dt |
= |
M |
. |
(3.6) |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
dt |
|
|
L × dt |
|
|
|
L |
|
||||||
Поскольку Ω << ω , |
можно считать, |
что и для неуравновешенного гироскопа |
|||||||||||||||
L = I ×ω , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
|
M |
|
|
. |
(3.7) |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
I ×ω |
||||||||||||
Методика измерений
Вращающий момент M задаётся сдвигом противовеса на чае момент внешних сил относительно точки O равен
M = mg × Dl ,
и с учётом (3.7) получим:
W = mg × Dl . I ×ω
Экспериментальная установка
l . В этом слу-
(3.8)
(3.9)
Установка представляет собой собственно гироскоп и сопряженные с ним измерительные системы и имеет следующие технические и метрологические данные:
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
29
диапазон управляемых оборотов двигателя 1000÷10000 об/мин;
диапазон измеряемого времени прецессии 1÷99999 мс;
диапазон измеряемого угла прецессии 10÷9900;
масса перемещаемого груза 0,6±0,05 кг; погрешность измерения времени 0,02%;
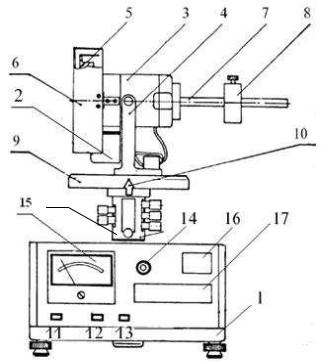
погрешность измерения скорости оборотов не больше 2,5%. Внешний вид гироскопа представлен на рисунке 3.2. На основании (1), ос-
нащенном ножками с регулируемой высотой, позволяющим произвести вырав-
нивание прибора, закреплена колонка |
|
|
с кронштейном и фотоэлектрическим |
|
|
датчиком №1, а также внешней втул- |
|
|
кой вращательного соединителя (18). |
|
|
Вращательный соединитель позволяет |
|
|
гироскопу обращаться вокруг верти- |
|
|
кальной оси и обеспечивает питание |
|
|
электрическим током фотоэлектриче- |
|
|
ского датчика №2 (2) и электрическо- |
18 |
|
го двигателя (3) посредством разъе- |
|
|
мов. Электрический двигатель смон- |
|
|
тирован на кронштейне (4) таким об- |
|
|
разом, что допускает вращения в вер- |
|
|
тикальной плоскости. На валу двига- |
|
|
теля закреплен ротор (5), защищае- |
|
|
мый экраном (6). Рычаг (7), закреп- |
Рис. 3.2 |
|
ленный на корпусе двигателя, имеет |
||
|
нанесенную метрическую шкалу. На рычаге закреплен груз (8). При помощи перемещения груза по рычагу можно уравновесить гироскоп, перемещая центр масс системы.
Поворот гироскопа вокруг вертикальной оси можно считывать с диска (9) с нанесенной угловой шкалой при помощи указателя (10). Диск (9) имеет на окружности отверстия через каждые 50, которые подсчитываются фотоэлектрическим датчиком №1, передающим информацию об угле поворота в блок управления и измерений. Ротор (5) имеет на окружности прорези, которые подсчитываются фотоэлектрическим датчиком №2, передающим информацию о скорости оборотов электрического двигателя в блок управления и измерений.
На лицевой панели блока управления имеются следующие элементы:
11(СЕТЬ) – выключение сети;
12(СБРОС) – сброс измерителя;
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
30
13(СТОП) – окончание измерений;
14(РЕГУЛЯЦИЯ СКОРОСТИ) – вращение потенциометром вызывает включение напряжения питания двигателя и управление скоростью оборотов двигателя;
15– показания частоты вращения двигателя, об/мин;
16 |
– |
показания угла оборота гироскопа вокруг вертикальной оси φ, град; |
17 |
– |
показания времени измерений t, с. |
Порядок выполнения работы
Задание 1. Измерение скорости прецессии и момента импульса гироскопа. Изучение зависимости скорости прецессии от момента силы.
1.С помощью регулируемых по высоте ножек установите основание прибора в горизонтальное положение.
2.Подключите прибор к питающей сети.
3.Нажмите клавишу СЕТЬ, при этом все индикаторы должны высвечивать цифру нуль.
4.Сбалансируйте гироскоп. Это делается путем перемещения противовеса (8) по стержню. Сбалансированный гироскоп должен находиться в положении безразличного равновесия, рычаг (7) гироскопа строго горизонтален. Запи-
шите l0 – положение груза, при котором гироскоп сбалансирован (от этого положения отсчитывается величина l ).
5.Включите питание двигателя.
6.Отрегулируйте обороты двигателя на ν=5000 об/мин. Следует выждать
2-3 минуты, |
чтобы |
вращение |
ротора стабилизировалось. Вычислите |
ω = 2π ×ν / 60 . |
|
l = 1 ñì |
|
7. Переместите груз 8 на |
влево или вправо. |
||
8.Удерживайте рычаг в исходном (горизонтальном) положении. Нажмите кнопку СБРОС и отпустите гироскоп.
9.После поворота гироскопа на угол φ=200 нажмите кнопку СТОП. Дождитесь остановки секундомера. Она происходит только при углах поворота, кратных 100.
10.Показания значений угла φ и времени t прецессии занесите в таблицу 3.1.
11.Нажмите кнопку СБРОС.
12.Повторите измерения (пункты 8-10) для одного и того же угла не менее 3 раз, рассчитайте среднее время.
13.По значениям φ и tср. вычислите угловую скорость прецессии:
Вологодский государственный технический университет
