Приливы Земной коры

Т.к. Земля не абсолютно твердое тело, то приливы есть и в земной коре. По их величине судят о степени твердости Земли. Движения коры фиксируются по отклонению отвесной линии. Так, для абсолютно твердой Земли отвес отклоняется на угол :

Для Луны: .

Для Солнца: .

Естественно, что наблюдаемые меньше этих значений вследствие нетвердости пород коры. Измерения показывают, что реальные углы равны 60 – 65 % от теоретических. Однако запаздывания почти нет, т.е. трение в коре для приливов мало. Приливы коры составляютот морских – теоретически. Измерения подтверждают эту оценку.

Приливы существуют также и в атмосфере Земли: 0,025 мм рт.ст. – от Луны; 0,01 мм рт.ст. – от Солнца.

Три типа приливов

(П. Мельхиор "Земные приливы" гл. 2)

Введение понятия потенциала приливообразующей силы (Лунного, Солнечного) позволяет ограничиться ее изучением и получением из нее характеристик того прилива, который мы хотим исследовать.

Однако выражение для W′ неудобно, поскольку построено на основе локальной координатыZ(зенитного расстояния) рассматриваемого возмущающего светила. Поэтому, используя сферический треугольник, построенный на Земле по точкам: полюс – зенит Луны – точка наблюдения (зенит), – подставим вместоZобычные экваториальные координаты (часовой уголHи склонение) и астрономические координаты места наблюдения (,). Тогда:

 – склонение – широта, над которой "стоит" светило.

H– долгота, над которой висит светило.

Последовательно получим

.

Тогда для угловой части потенциала W′ имеем:

Первые 3 члена (включая единицу) правой части выражения для перепишем так:

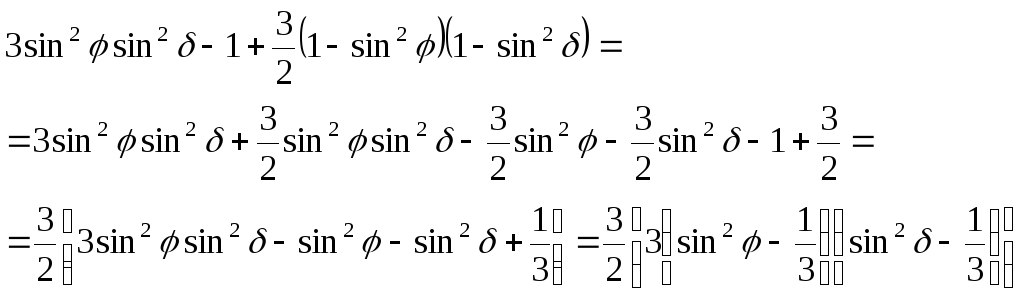
И теперь потенциал приливообразующей силы можно переписать ( с точностью до численного коэффициента):

Подобное разделение приливообразующего потенциала было впервые выполнено Лапласом. Он же дал их интерпретацию – каждого из трех членов потенциала.

Первая из этих функций (рис. а) имеет в качестве узловых линий (W′ = 0 илиg = 0) только меридианы, расположенные на ± 45º от меридиана светила. Сфера делится ими на 4 сектора с положительными и отрицательными (заштриховано) значениями. Это –«секториальная сферическая функция»,задающая приливы с полусуточным периодом с максимумом на экваторе при = 0. На полюсах функция становится нулевой. Лаплас назвал эти приливыприливами третьего типа. Важно, что они так перераспределяют массы на Земле, что ни положение полюса инерции, ни главный моментC(от которого зависит скорость вращения Земли) не изменяются.

Вторая функция (рис. б) имеет узловыми линиями меридиан (± 90º светила) и экватор. Максимальные значения у функции – на широтах ± 45º. Прилив имеет суточный период. На экваторе и полюсах функция всегда равна нулю. По Лапласу – это приливы второго типа. От приливов – изменяются положения полюса инерции, но главный моментC = const.

Третья, зональная функция (рис. в) зависит только от широты. Ее узловые линии – параллели ± 35º16′. Ее период равен для Луны – 14 суток, для Солнца – 6 месяцев. По Лапласу – приливы первого типа. Временная зависимость обусловлена зависимостью функции от склонения светила, которое меняется с движением светила (для Солнца ­– наоборот) вокруг Земли. Приливы вызывают изменения момента инерцииCи, значит, вариации в скорости вращения Земли с теми же периодами.

Уровенная поверхность здесь смещается вниз у полюса на ~28 см и приподнимается на экваторе на ~14 см. Смысл этого, так называемого, «постоянного прилива» состоит в дополнительном малом увеличении сжатия Земли.