Формула Стокса

Задачу определения высот геоида над эллипсоидом относимости по аномалиям силы тяжести впервые решил Стокс в 1849 году. Он получил интегральную формулу, дающую связь высот геоида и сфероида (эллипсоида) относимости с величинами аномалий силы тяжести – формулу Стокса. По аномалиям g на геоиде она позволяет в любой точке определить высоту геоида над эллипсоидом.

Формула Стокса «определяет» геоид – фигуру, которая в открытом океане есть истинная фигура Земли. И хоть геоид не есть «последнее» приближение к фигуре Земли – на материках он ничуть не лучше эллипсоида относимости, – все же это важная поверхность, разделяющая Землю на гладкую часть и на «слой», «поднятый» до физической поверхности Земли.

Итак, будем исходить из 13:

.

Перепишем это уравнение в виде: (помним, что в качестве «базового» потенциала в ее выводе взят потенциал шара):

.

Т.е.: .

Функция E – гармоническая, принимает на поверхности сферы  значения . Для так определенной (заданной на поверхности сферы) функции имеем во внешнем пространстве, согласно интегралу Пуассона, выражение:

14

(продолжили E аналитически в пространство вне поверхности , т.е. E() ).

Умножим обе части 14на rdr и проинтегрируем по всему внешнему пространству, т.е. по r от r до ∞. Именно здесь считаем определенной функцию E. Получаем:

15

Для справки: , Согласно сферической тригонометрии:

Для внутреннего интеграла в 15 интегрирование дает:

16

Здесь при подстановке неочевидны значения интеграла при . Однако, учитывая, что при больших r (см. рисунок)

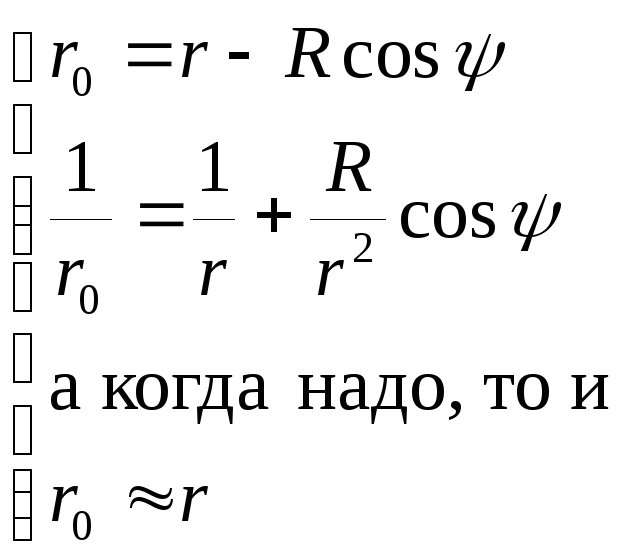
получим: .

В итоге, имеем (для больших r и, в частности, для r = ):

В принципе, даже в такой записи интеграл расходится. Однако, он есть лишь часть более сложной «конструкции»; а полный интеграл, по крайней мере на поверхности , имеет конечную величину.

Для правой части 15, в итоге, можем записать (для больших r):

.

Обратимся к левой части 15: .

Что имеем при для нее ?

Посмотрим, что представляет собой потенциал T. Здесь так же, как и при разложении W, имеем:

Аналогичен и физический смысл коэффициентов разложения, а именно:

k₀ – общая масса, создающая потенциал T. Но уровенная поверхность W = С (и геоид, и эллипсоид) заключает в себе всю массу Земли (см. выше теорему Стокса). Потенциал T между этими двумя поверхностями определяется не добавочной массой, а есть следствие различий в распределении масс для обеих тел. Поэтому общая сумма масс, создающая потенциал T, равна нулю. Следовательно: k₀ = 0.

При совпадении (совмещении) начала координат с центром масс и при учете, что центры масс геоида и сфероида совпадают, для k₁, как координаты центра масс получаем: k₁ = 0.

Тогда: и, следовательно: .

Отсюда следует, что левая часть 15 конечна, значит, и правая конечна при любых r.

Имеем (см. 16 – случай небольших r):

Разделим обе части на r² и обозначим:

.

Тогда:

.

Функция T определена. Она связывает потенциал T с аномалиями силы тяжести, являясь разностью потенциала притяжения между геоидом и сфероидом. Принимая r = R – для сферы с поверхностью , получим:

17

Действительно, так как r = R, то

.

Следовательно:

В итоге получаем функцию Стокса:

.

Подставим в 17: и , тогда:

18

Эта формула в 1849 г. была получена Стоксом. Она дает превышение геоида над сфероидом в точке при условии, что аномалии силы тяжести известны для всей поверхности Земли. Вычисление  производится численным интегрированием.

Для собственно Земли-шара , тогда

.

( – широта точки по отношению к точке P).

– эта функция табулирована. Тогда

19

R – средний радиус Земли;  – среднее значение силы тяжести на сфероиде, равное 979,77 Гал.

Предельные значения  – порядка сотни метров.

Графически функция F() выглядит:

Поскольку в 19 интегрирование ведется по всей Земле, то для каждого элемента интегрирования должно быть известно g. При этом, как видим из рисунка, влияние аномалий далеких от исследуемой точки областей остается существенным. Т.е. при пользовании формулой Стокса важно значениеg по всей Земле, т.е. и для далеких зон.

Однако далеко еще не вся Земля изучена в гравиметрическом отношении. Значительные области ее не покрыты даже редкими гравиметрическими съемками. Области океанов, особенно в Южном полушарии, на огромных площадях не имеют ни одного гравиметрического пункта. Приходится для этих "пустых" мест назначать гипотетические значения аномалий, полученных в тех или иных предположениях. Часто для всех неизученных областей полагают аномалии в свободном воздухе или изостатические аномалии равными нулю.

В настоящее время развитие вычислительной техники стимулирует построения выражений для превышений  в виде ряда:

.

Здесь и – коэффициенты разложения поля g в ряд.

В итоге, по экспериментальным значениям g опять определяем .

В вычислительные схемы вводится информация о g, отвечающая на поверхности Земли трапециям или менее – в зависимости от того, насколько хороша (полна) исходная информация.