Лабораторный практикум / Лаборатория радиофизики / - ПМФ - / 2 - Моделирование и исследование линейных систем / 2 - Описание

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ

НАПРАВЛЕНИЕ «ПРИКЛАДНЫЕ МАТЕМАТИКА И ФИЗИКА»

Описание лабораторной работы

МОДЕЛИРОВАНИЕ И ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СИСТЕМ

Санкт-Петербург

2008 г.

2

Введение

Целью данной работы является практическое освоение основных методов анализа линейных систем – временного и частотного. Для изучения основных особенностей применения указанных методов выбраны простейшие линейные системы – RC-фильтры первого порядка. Более сложные случаи рассматриваются в работах №3 «Активные фильтры», №4 «Усилители и генераторы низкочастотных сигналов» и №5 «Исследование колебательных контуров с индуктивной связью».

Работа состоит из двух этапов. На первом этапе выполняется компьютерное моделирование линейных систем. В качестве среды моделирования используется MATLAB и его пакеты расширения

SignalProcessingTooldox, Simulink, SimPowerSystem. С использованием этих программных средств строятся амплитудно-частотные, фазо-частотные, переходные и импульсные характеристики фильтров, моделируется прохождение через фильтры типовых сигналов.

На втором этапе работа фильтров исследуется экспериментально. Студенты самостоятельно спаивают рассчитанные фильтры и проводят измерения некоторых величин. Результаты компьютерных расчетов сравниваются с полученными экспериментальными данными. Измерения выполняются как с использованием аналоговых, так и цифровых приборов. В последнем случае используется возможность записи данных в файл и их дальнейшей обработки в MATLAB.

Линейные системы

Под линейными понимают такие системы, параметры которых не зависят от величины распространяющихся в них сигналов. Строго говоря, любая система является нелинейной, однако в случае распространения малых сигналов нелинейными эффектами, как правило, можно пренебречь.

Если размеры системы достаточно малы (по сравнению с длиной волны распространяющихся в ней сигналов), то можно не учитывать волновой характер протекающих в ней процессов, в частности излучение сигнала в окружающее пространство, и ввести понятие системы с сосредоточенными параметрами – сопротивлениями, конденсаторами и индуктивностями. В дальнейшем в этой работе мы будем рассматривать только линейные системы с сосредоточенными параметрами.

Процессы, протекающие в линейных системах, описываются линейными дифференциальными уравнениями, которые получаются из системы уравнений Кирхгофа для контуров и узлов. В общем случае для линейной системы с сосредоточенными параметрами дифференциальное уравнение имеет следующий вид:

где y(t) – выходной сигнал при произвольном входном воздействии x(t).

3

Порядок дифференциального уравнения определяет порядок линейной системы. Заметим, что порядок дифференциального уравнения не может превышать число реактивных элементов в схеме.

Из курса математики известно, что общее решение y(t) дифференциального уравнения (1) представляет собой сумму общего решения y1(t) однородного уравнения

с ненулевыми начальными условиями

y(0) = a1 , y'(0) = a2 , K, yn−1(0) = an

ичастного решения y2(t) неоднородного уравнения (1) с нулевыми начальными условиями. Другими словами, выходной сигнал можно представить в виде суммы реакций системы на ненулевые начальные условия

ина входной сигнал. Ненулевые начальные условия реализуются тогда, когда к моменту включения входного сигнала t=0 в реактивных элементах схемы (индуктивностях и емкостях) была запасена энергия. Такие случаи встречаются достаточно редко, и мы в дальнейшем будем предполагать

начальные условия нулевыми, поэтому y1(t)ª0 и, следовательно, y(t)=y2(t), т. е. источником выходного сигнала является только входное воздействие.

Опираясь на принцип суперпозиции, можно решить задачу о том, как в общем виде определить выходной сигнал y(t) при произвольном входном воздействии x(t) для произвольной линейной системы. Принцип суперпозиции заключается в следующем: если на вход линейной системы

воздействуют одновременно несколько сигналов x1, x2, …, x n, то выходной сигнал будет представлять собой сумму сигналов y1, y2, …, y n, где yk есть реакция системы на входное воздействие xk при отсутствии остальных.

Эту задачу можно решить в общем виде, если удастся представить входное воздействие в виде суммы "стандартных" сигналов и определить реакцию системы на это стандартное воздействие. Можно выделить два подхода к решению данной задачи: временной и частотный методы.

Временной метод

В этом случае задача определения сигнала на выходе линейной системы решается во временной области, свойства системы описываются ее импульсной или переходной характеристикой.

Возьмем сначала в качестве стандартных сигналов ступенчатую функцию 1(t-T), включаемую в момент времени t=T (Рис. 1,а). Любой входной сигнал можно представить в виде набора сигналов такой формы (Рис. 1,б). Очевидно, что нижний заштрихованный сигнал равен x(0)1(t).

4

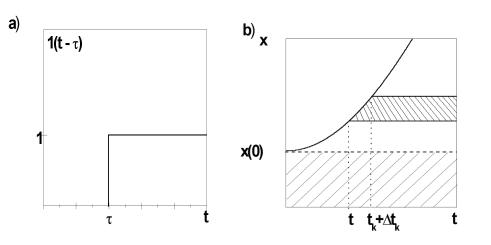
Рис. 1.

воздействие в виде функции единичного включения x(t)=1(t). Обозначим такую реакцию y(t)=h(t) и назовем функцию h(t) переходной характеристикой линейной системы. О том, как ее можно найти и каковы ее свойства, будет сказано ниже.

Зная переходную характеристику системы, можно определить выходной сигнал. Используя представление x(t) в виде (3) и учитывая принцип суперпозиции, получим

y(t) ≈ x(0)h(t) + ∑ x '(tk )h (t − tk ) t

Данное выражение, называемое интегралом Дюамеля, дает нам решение поставленной задачи.

В качестве другого стандартного входного воздействия выберем сигнал

системы на такое воздействие обозначим g t (t) . 5

Рис. 2

Заштрихованная часть входного сигнала, представленного на Рис. 2б,

Следовательно, приближенное выражение для выходного сигнала будет иметь вид:

y(t) ≈ ∑ x(tk )g t (t − tk ) t

функцию δ (t) . Получающийся при этом выходной сигнал обозначим g(t) и назовем импульсной характеристикой системы. Тогда выражение для

выходного сигнала y(t) будет представлять собой свертку входного сигнала и импульсной характеристики системы:

t

y(t) = ∫ x(τ )g(t −τ )dτ

линейной системы представляют собой ее реакцию на входные воздействия, равные нулю при t < 0 . Следовательно, в силу принципа причинности

(сигнал на выходе не может появиться раньше, чем на входе) h(t) и g(t) также равны нулю при t < 0 .

Частотный метод

В этом случае задача решается с применением спектральных разложений. Способ замены произвольного входного сигнала суммой стандартных воздействий основан на представлении функции рядом или

6

интегралом Фурье. Предположим, что входной сигнал – периодическая функция с периодом T. Любой реальный периодический сигнал может быть представлен в виде ряда Фурье

Отдельные слагаемые в рядах (9) и (11) называют гармониками. Выходной сигнал может быть определен в общем виде, если нам известна реакция

системы на гармоническое входное воздействие e−iωt при всех значениях частоты.

Пусть на вход линейной системы подается гармоническое воздействие

выходного и входного гармонических сигналов называется коэффициентом передачи линейной системы

Следовательно, модуль коэффициента передачи равен отношению амплитуды сигнала на выходе |B| к амплитуде сигнала на входе |A|, а его фаза

равна разности фаз указанных сигналов. Зависимость K (ω) называется

амплитудно-частотной характеристикой линейной системы (АЧХ), а фазо-частотной характеристикой (ФЧХ).

Если коэффициент передачи известен, то в силу принципа суперпозиции мы можем записать следующее выражение для выходного сигнала:

n

7

Итак, для решения задачи о прохождении сигнала произвольной формы через линейную систему с сосредоточенными параметрами можно предложить два метода:

1. Теоретически или экспериментально определить переходную h(t) или импульсную g(t) характеристику линейной системы и с помощью

выражений (5) или (8) рассчитать выходной сигнал; либо решить дифференциальное уравнение (1) непосредственно. В этом случае задача решается в терминах переменной t , поэтому такой метод называется временным.

2. Теоретически или экспериментально определить комплексный

коэффициент передачи & ( ω ) ; рассчитать амплитуды спектральных

K i

составляющих входного сигнала Dn для периодического сигнала или спектральную функцию X (iω ) для непериодического сигнала,

воспользовавшись выражениями (14) или (18), (19), определить выходной сигнал. В этом случае входной сигнал задается своим спектром, а свойства линейной системы передаются функцией частоты – коэффициентом передачи. Поэтому такой метод расчета выходного сигнала называется спектральным (частотным).

В лабораторной работе необходимо рассмотреть свойства простейших RC-цепей, используя как частотный, так и временной метод их анализа.

Методы измерения характеристик линейных цепей

Обсудим вопрос о том, как характеристики линейной цепи могут быть найдены экспериментально.

1. Коэффициент передачи. Для того чтобы определить коэффициент передачи K (iω) , нужно подать на вход системы гармонический сигнал A cos(ωt) и измерить параметры выходного сигнала, который в силу линейности системы также будет гармоническим B cos(ωt +ψ ) . Отношение амплитуд выходного и входного сигналов будет равно модулю коэффициента передачи на данной частоте, а разность фаз сигналов – фазе коэффициента передачи (13). Проведя такие измерения в выбранном диапазоне частот, мы узнаем АЧХ и ФЧХ системы в этом диапазоне.

2. Переходная характеристика h(t). По определению переходной характеристики, для ее измерения, нужно подать на вход системы единичное ступенчатое воздействие (функцию Хэвисайда) 1(t) , тогда сигнал на выходе будет представлять собой функцию h(t). На практике вместо такого входного сигнала подают последовательность прямоугольных импульсов, выбирая длительность импульса достаточно большой так, чтобы к моменту выключения импульса можно было считать переходные процессы в цепи практически закончившимися (т.е. чтобы напряжения на всех элементах и токи через них приняли к этому времени установившиеся значения).

9

3. Импульсная характеристика δ (t) . Чтобы экспериментально определить импульсную характеристику, нужно подать на вход системы воздействие, близкое к δ -функции. В качестве критерия "близости" сигналов можно выбрать критерий близости их спектров. Так как спектр δ -функции есть константа во всем диапазоне частот, то для определения импульсной характеристики нужно выбрать такой сигнал, спектральная плотность которого неизменна в достаточно широком диапазоне частот. Поясним это подробнее. Пусть нам необходимо определить импульсную характеристику фильтра нижних частот, АЧХ которого представлена на Рис. 3,а.

Рис. 3. Выбор характеристик входного сигнала для измерения δ (t) .

Возьмем в качестве входного импульсный сигнал прямоугольной формы единичной амплитуды и длительности τ И . Выражение для его спектра имеет вид (Рис. 3,б):

X (iω) определяется длительностью сигнала ω1 = 2π /τ И . Если этот нуль находится по оси частот существенно дальше граничной частоты фильтра ω0

(частоты, на которой модуль коэффициента передачи в 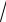2 раз меньше максимума) (Рис. 3,в), то в полосе пропускания фильтра спектр входного сигнала будет практически постоянным. Это означает, что такой входной сигнал может приближенно считаться δ -функцией для данной системы, а соответствующий ему выходной сигнал – импульсной характеристикой.

Лабораторная установка

Блок-схема лабораторной установки показана на Рис. 4.

10