
Билет № 1 Теплотехника и ее роль в народном хозяйстве. Основные понятия термодинамики.
Теплотехника- это наука о законах получения, распределения и преобразования тепловой энергии.
Теплотехника является общетехнической дисциплиной, которая занимает одно из центральных мест в инженерной подготовке специалистов. Это обусловлено тем, что процессы получения , использования и переноса теплоты имеют место практически во всех технических устройствах и технологических процессах современной техники. При расчете двигателей различных типов, холодильных и турбокомпрессорных установок, проектировании технологических процессов производства строительных материалов и дорожных одежд, восстановлении деталей и др. Современный специалист должен уметь правильно формулировать и решать разнообразные прикладные задачи с использованием основных законов термодинамики и тепломассообмена.
С РАЗВИТИЕМ электрификации и химизации в СССР роль теплотехники с каждым годом возрастает. Мощные паротурбинные установки на электростанциях с применением пара высоких параметров, внедрение комбинированных установок с одновременным использованием в качестве рабочих тел как водяного пара, так и продуктов сгорания различных топлив, теплофикация городов, развитие реактивных двигателей и газотурбинных установок, широкое внедрение в народное хозяйство двигателей внутреннего сгорания, отвод огромных тепловых потоков в ядерных реакторах для получения электроэнергии, большое строительство пищевых и химических предприятий, где продукты сгорания и водяной пар являются теплоносителями, переход к промышленному использованию магнитогидродинамического метода для непосредственного преобразования теплоты в электрическую энергию, широкое использование в народном хозяйстве холода и многие другие проблемы современной науки и техники необычайно расширили область теплотехники и все время ставят перед ней новые исключительно важные физические задачи.
ОСНОВУ термодинамики составляют фундаментальные законы природы. Сформулированные в термодинамических понятиях, они называются законами или началами термодинамики. На основе термодинамики разрабатывают новые и совершенствуют существующие тепловые машины и установки и создают высокоэффективные технологии, обеспечивающие экономное расходование энергетических и материальных ресурсов. Совокупность инженерных приложений
термодинамики образует ее раздел, называемый технической термодинамикой.
Билет № 2 Основные термодинамические параметры состояния рабочего тела. Термическое уравнение состояния.
ПАРАМЕТРЫ состояния
Абсолютное давление- интенсивная величина, характеризующая среднюю по времени силу, с которой частицы системы действуют на единицу площади стенки сосуда, в котором заключена система.
Давление- абсолютное, которое складывается из показаний прибора.
Pабс. = Ратм. + Ризб. Рабс. = Ратм. – Рвак.
Абсолютная температура- интенсивная величина, пропорциональная средней кинетической энергии частиц (молекул газа), из которых состоит система.
Термодинамическая температура: Т= t+273,15
Удельный объем- интенсивная величина, представляющая собой отношение объема системы V, к заключенной в нем массе М.
v=V/M V-объем системы М- масса
Плотность- величина, обратная удельному объему
р(ро)=1/v=M/V
УРАВНЕНИЕ состояния: F(p,v,T)=0
Билет №3
3) Термодинамический процесс. Обратимые и необратимые процессы. Термодинамическая система.
Определение: Если в термодинамической системе меняется хотя бы один из параметров любого входящего в систему тела, то в системе происходит термодинамический процесс.
Обратимые и необратимые процессы
Обратимый процесс — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.
Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.
Обратимые процессы дают наибольшую работу. Бо́льшую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.
Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности.
Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, термодиффузия, теплопроводность, вязкое течение и др. Переход кинетической энергии макроскопического движения через трение в теплоту, то есть во внутреннюю энергию системы, является необратимым процессом.
Термодинамическая система
Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом.
Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.
Для описания термодинамической системы вводят так называемые термодинамические величины — набор физических величин, значения которых определяют термодинамическое состояние системы.
Примерами термодинамических величин являются:
температура
давление
объем
внутренняя энергия
энтропия
энтальпия
свободная энергия Гельмгольца
энергия Гиббса
Если термодинамическое состояние системы не меняется со временем, то говорят, что система находится в состоянии равновесия. Строго говоря, термодинамические величины, приведённые выше, могут быть определены только в состоянии термодинамического равновесия
Термодинамические системы подразделяются на однородные по составу (например, газ в сосуде) и неоднородные (вода и пар или смесь газов в сосуде).
Выделяют также изолированные системы, то есть системы, которые не обмениваются с окружающей средой ни энергией, ни веществом, и закрытые системы, которые обмениваются со средой только энергией, но не обмениваются веществом. Если же в системе происходят обменные процессы с окружающей средой, то её называют открытой.
Билет №4 Теплота и работа как формы передачи энергии. Аналитическое выражение и графическое изображение.
Тела, участвующие при протекании т/д процесса обмениваются энергией. Передача энергии от одного тела к другому происходит двумя способами.
1-й способ реализуется при непосредственном контакте тел, имеющих различную температуру, путем обмена кинетической энергией между молекулами соприкасающихся тел либо лучистым переносом внутренней энергии излучающих тел путем э/м волн. При этом энергия передается от более нагретого к менее нагретому.
Количество энергии, переданной 1-м способом от одного тела к другому, называется количеством теплоты – Q [Дж], а способ – передача энергии в форме теплоты.
2-й способ связан с наличием силовых полей или внешнего давления. Для передачи энергии этим способом тело должно либо передвигаться в силовом поле, либо изменять свой объем под действием внешнего давления, То есть передачи энергии происходит при условии перемещения всего тела или его части в пространстве. При этом количество переданной энергии называется работой – L [Дж], а способ передача энергии в форме работы.
Количество энергии, полученное телом в форме работы называется работой совершенной над телом, а отданную энергию – затраченной телом работой.
Количество теплоты, полученное (отданное) телом и работа, совершенная (затраченная) над телом, зависят от условий перехода тела из начального состояния в конечное, т.е. зависят от характера т/д процесса.
Работа - есть фунцкия состояния вещества, т.е зависит от вида процесса.
Если поршень перемещается в цилиндре из т.А в т.В, то в процессе а-b происходит изменение состояния вещества.

Расширенное
элементарное перемещение
![]()
![]()
![]()
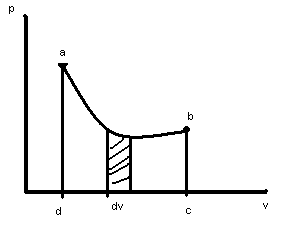
С математической точки зрения, этот интеграл равен площади фигуры лежащей под кривой.
Если v
в процессе увелич., то раб.
![]() ,dv>0
,dv>0
Если v
в процессе уменьш., то раб.![]() ,dv<0
,dv<0
Билет 9, 10
![]()
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.
Содержание
1 Молярная теплоемкость
2 Теплоемкость идеального газа в изопроцессах
2.1 Адиабатический
2.2 Изотермический
2.3 Изохорный
2.4 Изобарный
3 Вывод формулы для теплоемкости в данном процессе
4 См. также
Молярная теплоемкость
Молярная теплоемкость — теплоемкость 1 моля идеального газа.
![]()
![]()
Теплоемкость идеального газа в изопроцессах
Адиабатический
В адиабатическом
процессе теплообмена с окружающей
средой не происходит, то есть
![]()
. При изменении
объема температура и давление меняются,
то есть
![]() . Следовательно, теплоемкость идеального
газа в адиабатическом процессе также
равна нулю: Садиаб=0.
. Следовательно, теплоемкость идеального
газа в адиабатическом процессе также
равна нулю: Садиаб=0.
Изотермический
В изотермическом
процессе постоянна температура, то есть
![]() .
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности:
.
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности:
![]()
Изохорный
В изохорическом
процессе постоянен объем, то есть
![]() . Элементарная работа газа равна
произведению изменения объема на
давление, при котором происходит
изменение (δA = δVP). Первое Начало
Термодинамики для изохорического
процесса имеет вид:
. Элементарная работа газа равна
произведению изменения объема на
давление, при котором происходит
изменение (δA = δVP). Первое Начало
Термодинамики для изохорического
процесса имеет вид:
![]()
А для идеального газа
![]()
Таким образом,
![]()
где i — число степеней свободы частиц газа.
Изобарный
В изобарном процессе
():![]()
![]()
CP=δQ/νΔT=CV+R=((i+2)/2)*R
Вывод формулы для теплоемкости в данном процессе
Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу.
dU=δQ+δA, где δA — работа окр. среды над газом.
δAокр.среды=-δAгаза
δQ=dU+δAгаза
В расчете на 1 моль:
С=δQ/ΔT=(ΔU+pΔV)/ΔT
ΔU=CV*ΔT
C=CV+(pΔV/ΔT)в данном процессе
Билет 11: исследование изохорного процесса
Изохорным
называют процесс, в котором объем
рабочего тела остается постоянным.
Уравнение изохорного процесса имеет
вид
![]()
Примеры:1.нагрев или охлаждение в закрытом сосуде
2процесс горения топлива в бензинном двигателе
Связь параметров:
для процесса, протекающего между точками
1 и 2, находящимися на одной изохоре,закон
Шарля
![]()
Графическое
изображение:
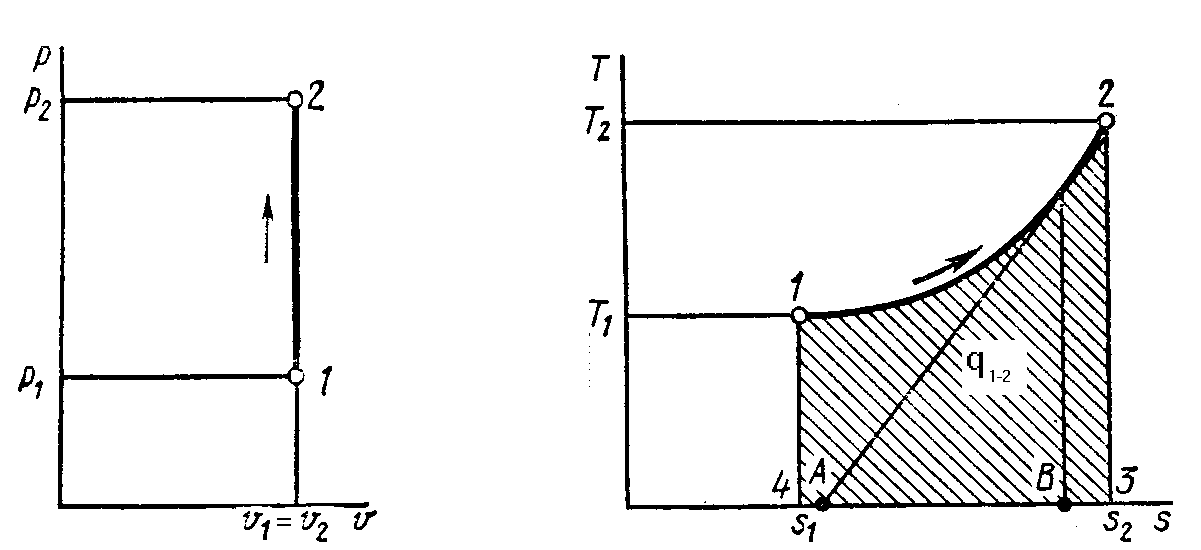
Тепло и работа: l=0,q=∆U+l,q=Cv* ∆T, ∆U=Cv*∆T
Энтропия при изохорном процессе: Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует:dS=dq/T
Билет 12:Исследование изотермического процесса
Называется процесс в котором температура рабочего тела постоянна
Пример: процесс кипения и конденсации
Уравнение процесса: PV=const,T=const
Связь параметров закон Бойля-Мариота:P1/P2= V2/V1
Графическое изображение:

Тепло и работа:q=∆U+l, ∆U=CV(T2-T1)=0

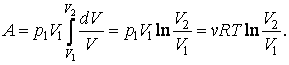
 A=l-работа
A=l-работа
13.Исследование адиабатного процесса.
Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.
Из первого начала
термодинамики (δQ=dU+δA) для адиабатического
процесса следует, что
![]() (1) т. е. внешняя работа совершается за
счет изменения внутренней энергии
системы.
(1) т. е. внешняя работа совершается за
счет изменения внутренней энергии
системы.
Используя
формулы δA=pdV и CV=dUm/dT,
для произвольной массы газа перепишем
уравнение (1) в виде
![]() применив дифференцирование уравнение
состояния для идеального газа pV=(m/M)RT
получим
применив дифференцирование уравнение
состояния для идеального газа pV=(m/M)RT
получим![]() (3)
(3)
Исключим
из (2) и (3) температуру Т.
![]() Разделив
переменные и учитывая, что Сp/СV=γ
, найдем
Разделив
переменные и учитывая, что Сp/СV=γ
, найдем![]()
Проинтегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, и потенцируя, придем к выражению
![]() или
или
![]()
Так как
состояния 1 и 2 выбраны произвольно, то
можно записать
![]() (4)
(4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Для
перехода к переменным Т, V или p, Т исключим
из (55.4) с помощью уравнения
Менделеева-Клапейрона
![]()
соответственно давление или объем:
![]() (5)
(5)
![]() (6)
(6)
Выражения (4) — (6)
представляют собой уравнения
адиабатического процесса. В них
безразмерная величина![]() (7) называется показателем
адиабаты
(или коэффициентом
Пуассона).
Для одноатомных газов (Ne, He и др.),
достаточно хорошо удовлетворяющих
условию идеальности, i=3, γ=1,67. Для
двухатомных газов (Н2,
N2,
О2
и др.) i=5, γ=1,4. Значения γ, вычисленные по
формуле (55.7), хорошо подтверждаются
экспериментом.
(7) называется показателем
адиабаты
(или коэффициентом
Пуассона).
Для одноатомных газов (Ne, He и др.),
достаточно хорошо удовлетворяющих
условию идеальности, i=3, γ=1,67. Для
двухатомных газов (Н2,
N2,
О2
и др.) i=5, γ=1,4. Значения γ, вычисленные по
формуле (55.7), хорошо подтверждаются
экспериментом.
Диаграмма
адиабатического процесса (адиабата)
в координатах р, V есть гипербола (рис.
1). На рисунке видно, что адиабата (pVγ =
const) более крута, чем изотерма (pV = const) по
причине, что при адиабатическом сжатии
1—3 увеличение давления газа обусловлено
не только уменьшением его объема, как
при изотермическом сжатии, но и повышением
температуры. Вычислим работу, которую совершает газ
в адиабатическом процессе. Запишем
уравнение (1) в виде
Вычислим работу, которую совершает газ
в адиабатическом процессе. Запишем
уравнение (1) в виде
![]() Если газ адиабатически расширяется от
объема V1 до V2, то его температура
уменьшается от T1 до T2 и работа расширения
идеального газа
Если газ адиабатически расширяется от
объема V1 до V2, то его температура
уменьшается от T1 до T2 и работа расширения
идеального газа![]() Используя те же приемы, что и при выводе
формулы (5), выражение (8) для работы при
адиабатическом расширении можно привести
к виду
Используя те же приемы, что и при выводе
формулы (5), выражение (8) для работы при
адиабатическом расширении можно привести
к виду![]() где p1V1=(m/M)RT1
где p1V1=(m/M)RT1
Работа, которую совершает газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 2), меньше, чем при изотермическом, по причине, что при адиабатическом расширении осуществляется охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне такого же количества теплоты.
Рассмотренные изобарный, изохорный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны СV и Сp, в изотермическом процессе (dT=0) теплоемкость равна ±∞, в адиабатическом (δQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается неизменной, называется политропным.
14.Политропные процессы. Их графическое изображение в ρ-ν и Т-S диаграммах.
14 Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.
Для идеального
газа уравнение политропы может быть
записано в виде: pVn
= const где величина
![]() называется показателем политропы.
называется показателем политропы.
В зависимости от процесса можно определить значение n:
1. Изотермический процесс: n = 1, так как PV1 = const, значит PV = const, значит T = const.
2. Изобарный процесс: n = 0, так как PV0 = P = const.
3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.
Здесь γ — показатель адиабаты.
4. Изохорный процесс:
![]() ,
так как
,
так как
![]() ,
значит P1
/ P2
= (V2
/ V1)n,
значит V2
/ V1
= (P1
/ P2)(1
/ n) , значит,
чтобы V2
/ V1
обратились в 1, n должна быть бесконечность.
,
значит P1
/ P2
= (V2
/ V1)n,
значит V2
/ V1
= (P1
/ P2)(1
/ n) , значит,
чтобы V2
/ V1
обратились в 1, n должна быть бесконечность.
