─ 5 ─

Задача 1. Нестационарная теплопроводность

Металлическая заготовка, имеющая форму пластины, неограниченной длины и высоты толщиной с начальной температурой , нагревается в печи, температура которой поддерживается постоянной до конечной температуры по оси заготовки . Считая длину и высоту заготовки большими по сравнению с толщиной, определить:

1. Время нагревания заготовки до данной конечной температуры;

2. Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина);

3. Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул);

4. Количество теплоты, подведённой к телу в течении всего периода нагревания (на 1 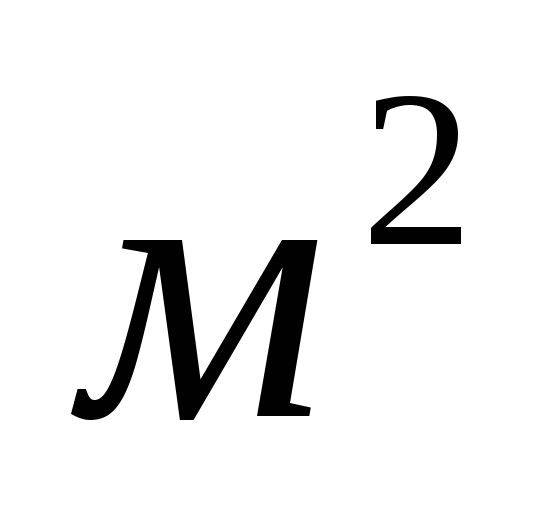поверхности пластины или на 1 длинны циллиндра);

5. По результатам (2) и (3) построить графики.

1._Определение времени нагревания заготовки до конечной температуры

Вычислим число и безразмерную температуру для центра пластины в последний момент времени нагрева:

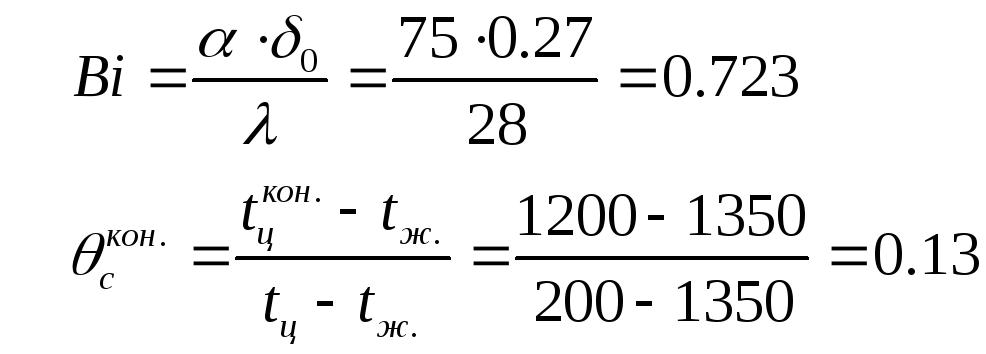
По номограмме Будрина для середины пластины определим (рис. 1):

Вычислим время нагревания заготовки:

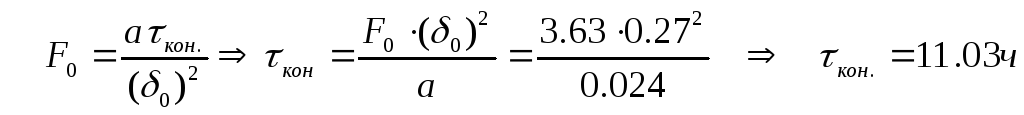
2._Определение температур на оси и на поверхности заготовки для различных моментов времени

Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от и ). По безразмерным температурам вычислим температуры в центре и на поверхности пластины в градусах Цельсия.

Для :

1. Время нагревания

2. Безразмерная температура в центре пластины (определяем по соответствующей номограмме Будрина (рис.1.) в зависимоси от и ):

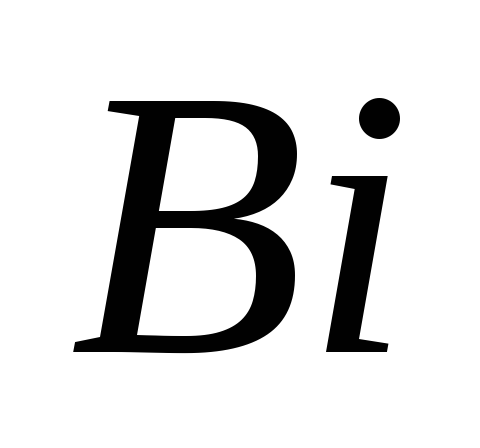3. Безразмерная температура на поверхности пластины (определяем по соответствующей диаграмме Будрина (рис.2.) в зависимоси от 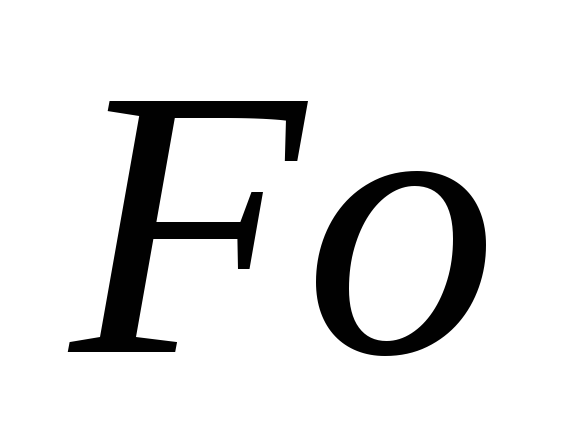и ):

4. Температура в центре пластины:

5. Температура на поверхности пластины:

Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу.

	0.6	1.2	1.8	2.4	3.0	3.63
	1.82	3.65	5.47	7.29	9.11	11.03
	0.76	0.53	0.39	0.28	0.19	0.13
	0.57	0.38	0.27	0.197	0.146	0.095
	476	740.5	901.5	1028	1131.5	1200
	694.5	913	1039.5	1123.5	1182.1	1240.8

3._Определение распределения температуры по толщине заготовки для четырёх моментов времени

Для (т.к. заготовка имеет форму пластины), для вычисления безразмерной температуры можно ограничится одним членом ряда:

По значению числа Био из таблицы рис.3 выбираем постоянные ,,,

При определим из таблиц:

0.723	1.094	0.760	0.578	0.792

Толщину пластины разбиваем на 4 слоя. Тогда безразмерные координаты расчетных точек будут равны:

(середина пластины), ; ; ; (поверхность пластины).

При и :

1. Аргумент косинуса (в радианах):

2. Косинус, вычисленный в этом аргументе:

3. Безразмерная температура для этой точки:

4. Температура для этой точки:

Для остальных точек и в другие моменты времени вычисления производим аналогичным образом, результаты записываем в таблицу.

			0	0.25	0.5	0.75	1
			0	0.19	0.38	0.59	0.76
			1	0.9820	0.9287	0.8309	0.7248
0.6	1.82		0.7734	0.7595	0.7183	0.6426	0.5606
			460.59	476.60	524.01	610.99	705.36
1.8	5.47		0.3864	0.3796	0.3590	0.3212	0.2802
			905.50	913.50	937.19	980.66	1027.82
3.0	9.11		0.1932	0.1897	0.1794	0.1605	0.1400
			1127.85	1131.85	1143.96	1165.41	1188.98
3.63	11.03		0.1342	0.1318	0.1246	0.1115	0.0973
			1195.65	1198.43	1206.66	1221.75	1238.13

Строим график изменения температуры по сечению пластины для выбранных моментов времени

4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 квадратный метр поверхности пластины)

Полное количество теплоты, которое было бы подведено к пластине (на 1 квардратный метр её поверхности), если бы нагревание длилось до наступления полного теплового равновесия между пластиной и воздухом печи:

Средняя безразмерная температура в последний момент времени нагревания ().

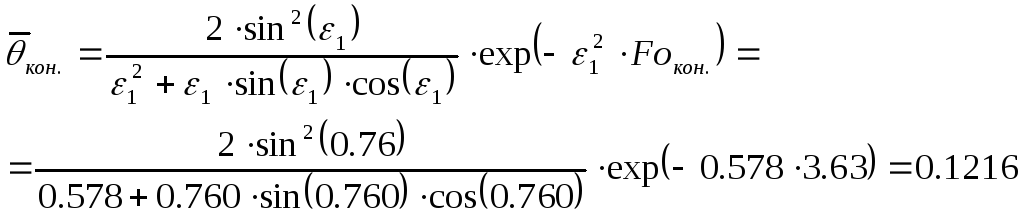
Полное количество теплоты, подведённое к пластине (на 1 квадратный метр её поверхности) за весь период нагрева:

5._Графики, построенные по данным пунктов 2 и 3

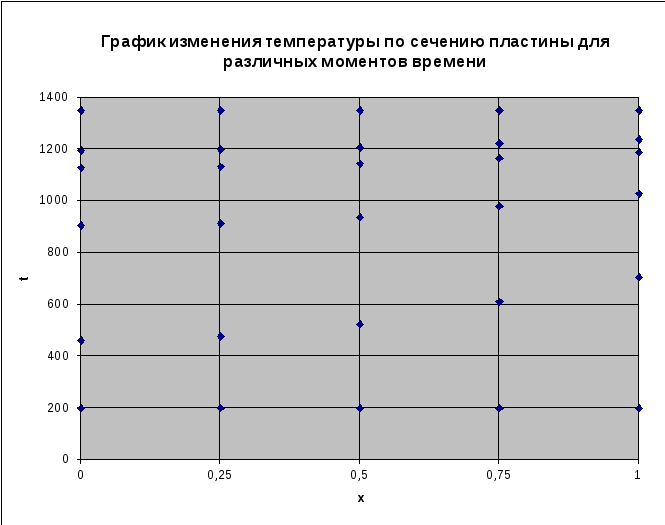
Рис. 1 Зависимость для середины тонкой пластины

Рис. 2 Зависимость для поверхности тонкой пластины

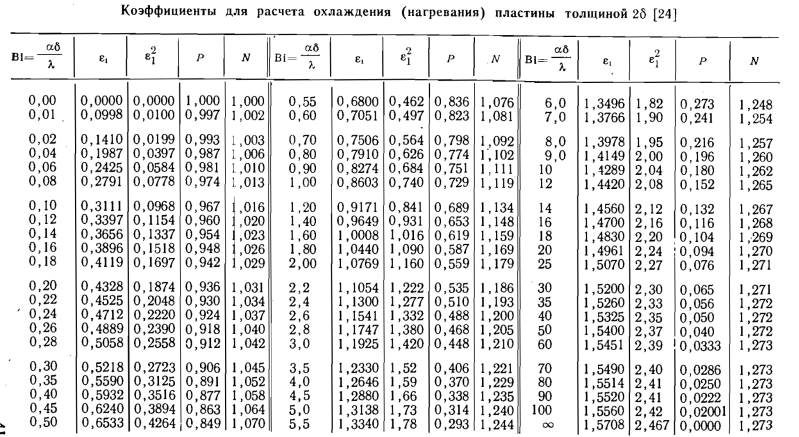
Рис. 3.