Подход к изучению таблицы умножения, предложенный а. М. За­харовой и т. И. Фещенко (применим к традиционной программе).

Остановимся на некоторых приемах составления и запоминания таблиц более подробно.

Начинать составление таблиц умножения с изучения умножения числа 9 имеет смысл, так как именно ее запоминание для детей вызывает наибольшие трудности. Именно здесь важно обратить внимание детей, как можно получить каждый результат, показать различные способы рассуждений.

9 ∙2 = 18

9∙3= 9 + 9 + 9 = 9∙2+9=18 + 9 =27, 9∙3=27

9∙4= 9 + 9 + 9 + 9=9∙3 + 9=27+ 9= 36, 9∙4= 36

9∙5= 9 + 9 + 9 + 9 + 9=9*4+ 9 = 36 + 9 =45, 9∙5=45

9∙6= 9 + 9+9 + 9 + 9 + 9 = 9∙5 + 9 = 45 + 9 = 54, 9∙6=54

9∙7= 9 + 9 + 9 + 9 +9 + 9 + 9 = 9∙6 + 9 = 54 + 9 = 63, 9∙7=63

9∙8=9+9+9+9+9+9+9+9=9∙7+9=63+9= 72, 9∙ 8 = 72

9∙9=9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 9∙8 + 9 = 72+ 9 = 81 9∙9=81

После того как таблица составлена, полезно внимательно рассмотреть получившуюся справа колонку.

Итак, при умножении девяти на однозначное число (или при умножении однозначного числа на 9) получится 9 и число, сумма цифр которого равна. При умножении на 9 не может получиться результат 28, 35, 46 и т.д. Для ребенка это очень важный критерий дли самоконтроля.

После того как составлена таблица умножения 9, выписываются таблица умножения на 9 и соответствующие таблицы на деление. Теперь, кроме традиционных заданий, направленных на усвоение знания табличных случаев, можно предложить и такие:

1. Не выполняя вычислений, объясните, почему данные равенства не могут быть верными: 9 ∙6 = 55, 4 • 9 = 81, 5 • 9 = 44, 9∙7 = 72.

2. Выберите из данных чисел те, которые были получены в результате умножения числа на 9: 42, 56, 45, 37, 81. Какое число умножали на 9? Аналогичным образом рассматривается умножение числа 2. Подробно останавливаться на этом случае не будем, так как эта таблица запоминается всеми детьми без особого труда.

После составления таблицы умножения 4 имеет смысл обратить внимание учеников на два момента:

а) в этой таблице все произведения — четные числа, т.е. результатом умножения числа на 4 не может быть 13, 17, 25, 37 и т.д.;

б) часто лучше умножать не 4 на число, а воспользоваться сначала переместительным свойством умножения и умножать число на 4, а потом сочетательным свойством, т.е. умножить число на 2, а потом полученный результат умножить еще раз на 2.

Например, при вычислении произведения 4 • 6 можно рассуждать так:

1. Я помню, что 4 • 5 = 20, значит, 4∙6 = 4∙5 + 4 = 20 + 4 = 24.

2. Я знаю, что 4 ∙10 =40 и 4 ∙4 =16 Тогда 4 ∙6 = 4 • 10- 4 ∙4 = 40-16=24. После составления каждой новой таблицы полезно полученные результаты заносить в таблицу Пифагора.

Методическая система развивающего обучения математике

Н.Б. Истоминой

Методическая система Н.Б. Истоминой направлена на формирование приемов умственной деятельности и усиление содержательного аспекта обучения, на формирование общих способов действий, что способствует развитию вычислительной культуры — основы овладения прочными и осознанными вычислительными навыками.

Во II классе параллельно с разъяснением предметного смысла умножения начинается работа по формированию вычислительных навыков умножения.

Особенности методики формирования навыков табличного умножения заключаются в следующем:

1. Составление и усвоение таблицы умножения начинается со случаев умножения числа 9, что помогает сосредоточить внимание учащихся на наиболее сложных для запоминания случаях табличного умножения — 9 •8, 9 • 6, 9 • 7, 8 • 7, 7 • 6.

2. Составление таблицы осуществляется небольшими порциями.

3. Учитывая, что не все учащиеся могут непроизвольно запоминать табличные случаи умножения в процессе выполнения обучающих заданий, в учебнике в определенной системе даются установки на запоминание трех-четырех случаев табличного умножения.

4. Использование переместительного свойства умножения при составлении таблицы сокращает объем, и последняя таблица (умножение на 2) содержит только одну строку — 2 ∙ 2 = 4.

Формированию табличных навыков умножения способствует система заданий продуктивного характера, которая требует от учащихся активного использования приемов умственной деятельности, что оказывает по­ложительное влияние на непроизвольное запоминание табличных случаев умножения. Система заданий отражает сущностный подход к понятию вычислительная культура и реализуется в соответствии с закономернос­тями процессов понимания и запоминания изучаемого материала. Авторами разработана следующая система упражнений.

I. Упражнения, основанные на приеме использования стимулирующих звеньев, а именно:

1. Упражнения на соотнесение рисунка и числового выражения Закончи рисунок, соответствующий данному выражению, и найди его значение: 3 • 7 = ? 9 ∙5 = ? 8 ∙7 = ?

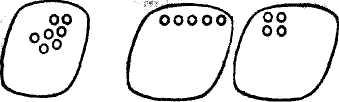
2. Упражнение на запись числового выражения по данному рисунку: Запиши выражения, которые соответствуют каждому рисунку и вычисли их значения:

3 ∙7 = ? 9∙5 = ? 8∙7 = ?

3. Упражнения на выбор числового выражения, соответствующего рисунку.

Найди рисунок, которому соответствует каждое выражение, и вычисли значения произведений:

6 ∙9 = ? 2 ∙8 = ? 3 ∙6 = ?

В процессе выполнения таких заданий активно включаются конкретно-образное и наглядно-действенное мышление, что оказывает положительное влияние на непроизвольное запоминание табличных случаев умножения.

П. Упражнения, основанные на приеме выделения смысловых опорных пунктов:

1. Вставь цифры в «окошки», чтобы получились верные равенства:

3 ∙7 = ?1 6 ∙8 = 4? 8 ∙8 = ?4

4• 8 = ?2 3 ∙7 = 2? 7•7=4?

7∙5=?5 7 ∙8=5? 5 • 9 = ?5

4 • 4 = ?6 9 ∙9 = 8? 8 ∙5 = 4?

2. Разгадай правило, по которому составлены схемы, и запиши числа в «окошки»:

Ориентировочной основой или опорным пунктом в каждом задании является математическая запись, с помощью которой учащиеся устанавливают связи между числовым выражением и его значением. Формулировка самого задания стимулирует активную работу мысли. Индивидуальные особенности памяти каждого ученика способствуют вариативности выполнения упражнения: либо ученик помнит наизусть таблицу умножения и только контролирует себя, записывая числа з «окошки», либо прибегает к общему способу действия (сложение одинаковых слагаемых), либо на основе переместительного свойства умножения пользуется опорными табличными случаями, которые были даны для произвольного запоминания.

III. Упражнения, в основе которых лежит прием реконструкции. (Под реконструкцией понимается любое эквивалентное изменение математического материала.)

Вычислительная деятельность предполагает не только формирование вычислительного навыка, но и использование его в различных ситуациях, разнообразие которых можно представить на любом арифметическом материале:

Вставь числа в «окошки», чтобы записи были верны:

9 •? =?+?+?+?+? 8 •? > 8 • ? 3 ∙8=? + ? + ?

?*8<?*9 8 ∙7>8*? ? + ? + ? + ? = 8•?

Анализируя числовые выражения, учащиеся, прежде всего, ориентируются на арифметическое действие. Вставляя пропущенное число, они могут пользоваться подбором, конкретным смыслом действия умножения по первому или второму множителю. Истинность полученной записи учащи­еся обосновывают с позиции общего способа действия умножения однозначных чисел. Вставь вместо звездочек знаки действий, чтобы равенства были верные:

7*2 = 7*7 7*3 = 7*7*7

6*2= 18*8 6*3 = 6*2*6

5*2 = 50*40 5*3 = 10*5

4*2 = 4*3*4 4*3 = 50*38

6*5 = 6*12*12 5*6 = 5*9*15

При выполнении таких упражнений учащиеся ориентируются на результат произведения и представляют полученное число в виде различных моделей с помощью арифметических действий. При этом совершенствуется навык умножения однозначных чисел, умения и навыки сложения и вычитания в области двузначных чисел.

Запиши каждое выражение в виде произведения двух чисел и найди его значение:

(34 - 27) • 8 = ?•? = ? (83 - 75) • 6 = ?•? = ?

(42-36)*5 = ?*? = ?

(129 -124) *3 = ?•? = ? (21-19) ∙4 = ?•? = ? (81-72)-7 = ?-? = ?

Совершенствование навыков табличного умножения можно широко использовать в процессе выполнения действий в выражениях со скобками, где действие в скобках заменяется его значением, и нахождение результата сводится к табличным случаям умножения, например:

1. Покажи с помощью скобок, произведение каких чисел заменили его значением:

6 ∙8 ∙3 = 48 ∙3

6 ∙8 ∙3 = 6 ∙24

63 • 4 = 7 ∙ 9 ∙4

7 ∙36 = 7 ∙9 ∙4

2. Вставь знаки >, < или =:

7 + 7 + 7... 7 ∙3

3 + 3 + 3 + 9 + 3... 7 ∙3

7 ∙5...5+5+5+5+5+5+5+5

7 ∙7... 7 ∙8-7

Анализируя математические записи, учащиеся устанавливают их сходство и различие на основе конкретного смысла действия умножения. Числовые значения этих выражений помогают осознать тот факт, что число может быть представлено различными моделями арифметических действий. При выполнении таких упражнений совершенствуются навыки табличного умножения, сложения и вычитания.

IV. Упражнения, базирующиеся на приеме соотнесения.

Прием сводится к увязыванию изучаемого материала с прежними знаниями и отдельных частей нового друг с другом.