
матан
.pdf
§7. Приложения интеграла |
541 |
где ∂Ω — положительно ориентирована.
Доказательство. Положим в формуле Грина Q(x, y) = x, P (x, y) = −y. Тогда
|
|
∂Q |
− |
∂P |
dx dy = 2|Ω| = |
x dy − y dx. |
||||||
|
|
|
|
|
||||||||
∂x |
|
∂y |
||||||||||
Ω |
|
|
|
|
|
|
|
|
|
|
∂Ω |
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|Ω| = |
1 |
x dy − y dx. |
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
||||||
∂Ω
§7. Приложения интеграла
При помощи кратных интегралов можно вычислять такие физические величины, как масса, заряд, емкость, центр тяжести, момент инерции и т.д. Приведем некоторые примеры.
Пусть в некоторой ограниченной области D распределена некоторая масса с переменной плотностью ρ(x, y, z). Иначе
говоря, на D задана некоторая неотрицательная и непрерывная функция ρ(x, y, z). Величину
m(D) = |
ρ(x, y, z)dx dy dz |
D
называют массой D.
Можно иначе. Допустим мы умеем вычислять массу тел (или их частей). И пусть D — ограниченная область в R3. Говорят, что в D задано распределение масс с плотностью
ρ(x, y, z) ≥ 0, если P = (x, y, z) D выполнено
lim m(B(P, r)) = ρ(P ),
r→0 43 πr3
где B(x, r) — шар с центром в точке x радиуса r, 43 πr3 — объем этого шара.
Отметим, что в данном определении шары с центром в точке P можно заменить системой областей, стягивающихся в точку P .
Разобьем область D на подобласти ∆1, . . . , ∆n, так что D =
ni=1∆i.


§8. Площадь в криволинейных координатах |
543 |
yc = |
ρ(x, y, z) dx dy dz , |
zc = |
ρ(x, y, z) dx dy dz . |
||||
|
|
ρ(x, y, z)y dx dy dz |
|
|
ρ(x, y, z)z dx dy dz |
||
|
D |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
D |
|
|
При этом используются формулы вычисления центра тяжести системы материальных точек (x1, y1, z1), (x2, y2, z2), . . ., (xn, yn, zn) с массами m1, m2, . . . , mn, соответственно:
|
|
|
in=1 ximi |
|
|
|
|
xc = |
in=1 mi |
|
, |
|
|
|
in=1 yimi |
|
in=1 zimi |
|||
|
|
|
|
|
|
|
yc = in=1 mi , zc = |
in=1 mi . |
|||||
Далее, пусть на плоскости задана кривая γ R2 и функция ρ(x, y) распределения масс на кривой γ. При этом плотность ρ(x, y) в точке (x, y) γ определяется как предел отношения ∆m части дуги, лежащей в окрестности точки (x, y) к длине этой же части дуги ∆l, когда окрестность стягивается к точке (x, y), т.е. ∆l → 0. Разбивая дугу γ на части γi и считая ρ постоянной на каждой дуге γi, можно найти массу
m(γi) ≈ ρ(ξi)· дл.γi, где ξi γi. Суммируя эти приближенные равенства и переходя к пределу при мелкости разбиения
стремящейся к 0, находим
m(γ) = ρ(x, y) ds.
γ
ПРИМЕР 1. Найти массу дуги γ : y = ln x, x [x1, x2], если плотность распределения равна квадрату абсциссы точ-
ки. |
x2 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m = x2 1 + |
|
1 |
|
dx = x |
|
|
||||||||
|
|
1 + x2 dx = |
||||||||||||
|
|
|
||||||||||||
x2 |
||||||||||||||
|
|
x1 |
|
x2 |
|
|
|
|
|
x1 |
|
|
|
|
1 |
3 |
|
|
1 |
|
3 |
3 |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
3 |
(1 + x2)2 |
x1 |
= |
3 |
(1 + x22)2 − (1 + x12)2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§8. Площадь в криволинейных координатах
ОПРЕДЕЛЕНИЕ 8.1. Пусть даны функции u = u(x, y), v = v(x, y), которые осуществляют непрерывное отображение области D плоскости (x, y) на область ∆ плоскости (u, v). Предположим, что существует обратное отображение x =
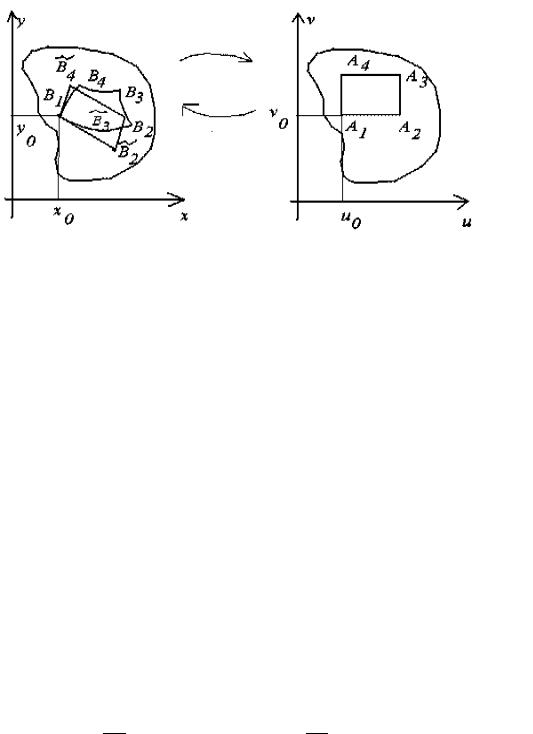
544 |
Глава 20. Теория интегрирования в Rn |
x(u, v), y |
= y(u, v), которое также является непрерывным, |
и каждой точке N = (u0, v0) ∆ соответствует единственная точка M = (x0, y0) D. Таким образом, если заданы
числа (u0, v0), так что точка N = (u0, v0) ∆, то эти числа полностью определяют положение точки M = (x0, y0) D.
Эти числа (u0, v0) называются криволинейными координатами точки (x0, y0).
Приведем некоторые соображения (точнее, наводящие рассуждения) об изменении площадей элементарных площадок
при подобных отображениях. Пусть |
|
|||||||||||||
N = A1 = (u0, v0), A2 = (u0 + du, v0), |
|
|||||||||||||
A3 = (u0 + du, v0 + dv), |
|
A4 = (u0, v0 + dv), |
|
|||||||||||
и |
|
|
|
|
|
|
|
|
||||||
|
B1 = (x(u0, v0), y(u0, v0)), |
|
||||||||||||
B2 = (x(u0 + du, v0), y(u0 + du, v0)) ≈ |
|
|||||||||||||
≈ (x(u0, v0) + |
∂x |
|
|
|
|
∂y |
|
|||||||
|
(u0, v0) du, y(u0 |
, v0) + |
|
|
(u0, v0) du) = B2, |
|||||||||
∂u |
∂u |
|||||||||||||
B3 = (x(u0 + du, v0 + dv), y(u0 + du, v0 + dv)) ≈ |
||||||||||||||
|
|
|
|
∂x |
|
|
|
∂x |
|
|||||
≈ (x(u0, v0) + |
|
(u0, v0) du + |
|
(u0, v0) dv, |
|
|||||||||
∂u |
∂v |
|
||||||||||||
y(u0, v0) + |
∂y |
∂y |
|
|||||||||||
|
(u0, v0) du + |
|
|
(u0, v0) dv) = B3 |
, |
|||||||||
∂u |
∂v |
|||||||||||||
B4 = (x(u0, v0 + dv), y(u0, v0 + dv)) ≈ |
|
|||||||||||||
|
∂x |
|
|
|
|
∂y |
|
|||||||
≈ (x(u0, v0) + ∂v (u0, v0) dv, y(u0, v0) + ∂v(u0, v0) dv) = B4.



§9. Замена переменных в кратном интеграле |
547 |
ЗАМЕЧАНИЕ. Так как |D| > 0 и якобиан не меняет знак, то заключаем, что знак ориентации контура ∂∆ совпадает со знаком якобиана. Вообще, при положительном якобиане отображения из положительной ориентации какого-либо контура в области плоскости (u, v) следует положительная ориентация его образа в области переменных (x, y). При отрицательном якобиане, ориентация контура меняется в противоположную сторону.
ПРИМЕР 1. Вычислить площадь фигуры, заключенной между двумя спиралями r = ϕ, r = 2ϕ, 0 ≤ ϕ ≤ c, где (r, ϕ) — полярная система координат.
Заметим, что ∂∂((x,yr,ϕ)) = r. Тогда
|D| = r dr dϕ = |
|
c |
dϕ |
|
r dr = 2 |
|
(4ϕ2 |
− ϕ2) dϕ = |
||||||
|
|
|
|
|
2ϕ |
|
1 |
|
c |
|
||||
∆ |
0 |
|
|
|
|
|
ϕ |
|
|
|
|
0 |
|
|
|
|
3 |
|
0 |
c |
|
|
c3 |
|
|
|
|||
|
|
|
ϕ2 dϕ = |
|
|
|
||||||||
= |
|
|
|
. |
|
|
|
|||||||
2 |
2 |
|
|
|
||||||||||
§9. Замена переменных в кратном интеграле
Пусть R — прямоугольник со сторонами параллельными осям координат (u, v). Пусть x = x(u, v), y = y(u, v) — дважды непрерывно дифференцируемое отображение в некото-
рой области, содержащей прямоугольник R вместе с границей и имеющее положительный якобиан. Предположим,
что данное отображение взаимнооднозначно переводит прямоугольник R в некоторую область D с границей ∂D. Очевидно, что ∂D — кусочно-гладкая кривая. Справедливо следующее утверждение.
ТЕОРЕМА 9.1. Пусть f(u, v) — произвольная интегрируемая по Риману на R функция. Тогда
f(u, v) du dv = |
f(u(x, y), v(x, y))∂(x, y) dx dy. (1) |
|
|
|
∂(u, v) |
R |
D |
|
Доказательство. Пусть u = u(x, y), v = v(x, y) обратное отображение к отображению x = x(u, v), y = y(u, v). Устроим разбиение P прямоугольника R прямыми параллельными осям координат, Ti — прямоугольники разбиения P . Так как



550 |
Глава 20. Теория интегрирования в Rn |
Вэтом случае векторное поле ϕQ называется потенциальным. Равенства (1) равносильны тому что
Q Q Q U = ϕQ = P i + Qj + Rk
(только в случае декартовой системы координат).
ТЕОРЕМА 10.1. Пусть в области G R3 задано непрерывное векторное поле ϕQ = (P, Q, R). Тогда следующие утверждения эквивалентны:
1.Векторное поле ϕQ потенциально.
2.Вдоль любого замкнутого ориентированного контура
C, лежащего в G выполнено
|
|
Q |
|
ϕ,Q ds = 0. |
|
|
C |
|
3. Пусть A0 G — фиксированная точка. Тогда инте- |
||
грал |
|
|
|
ϕ,Q dsQ |
|
CA0A
по каждой ориентированной кусочно-гладкой кривой CA0A G с началом в точке A0 и концом в точке A зависит от точек A0 и A, но не зависит от формы кривой. При этом
V (A) = V (x, y, z) = P dx + Q dy + R dz
CA0A
является потенциальной функцией векторного поля
ϕQ.
Доказательство. Очевидно, что из условия 3) следует справедливость 1), т.к. V (x, y, z) является потенциальной функцией.
Покажем, что из условия 1) следует выполнение условия 3). Из 1) следует существование непрерывно дифференцируемой функции U(x, y, z), такой что U = ϕQ. Рассмотрим произвольную кривую CA0A, соединяющую точки A0 и A. Предположим, что кривая CA0A задана параметрически уравнениями
,
