2. Методы прогнозной экстраполяции

Экстраполяция (распространение прошлых и настоящих закономерностей на будущее) является наиболее распространённым методом краткосрочного прогнозирования экономических явлений.

Выделяют следующие методы экстраполяции:

• экстраполяция по темпу роста;

• экстраполяция по темпу прироста;

• аппроксимация динамического ряда аналитическими кривыми;

• адаптивные методы.

При использовании методов экстраполяции исходят из предположения, что динамика развития объекта прогнозирования отмеченная за последние годы сохранится также и на ближайшую перспективу.

1. Экстраполяция по темпу роста

Возможны два варианта экстраполяции по темпу роста.

Вариант А. Прогнозное значение определяется по формуле:

,

где - темп роста, который находится из выражения:

,

здесь - значение показателя текущего периода;

- значение показателя предыдущего периода.

Вариант Б. Если имеется динамика за ряд предшествующих периодов, то можно использовать усредненный темп роста:

, .

Пример. Данные об объеме реализации автомобилей фирмой «Шумахер» за последние пять лет приведены в таблице 6.

Таблица 6

Объем продаж автомобилей фирмой «Шумахер»

Порядковый номер,	1	2	3	4	5
Год	2001	2002	2003	2004	2005
Количество проданных автомобилей, шт.	1280	1350	1480	1550	1660

Необходимо составить прогноз объёмов продаж на 2006 год.

Решение:

Вариант А: ;.

Вариант Б: ;.

2. Экстраполяция по темпу прироста

В данном случае также возможно применение нескольких вариантов расчета значения прогнозируемого параметра.

Вариант А. Прогнозное значение определяется по формуле:

,

где - темп прироста, который находится из выражения:

.

Вариант Б. Если имеется динамика за ряд предшествующих периодов, то можно использовать усредненный темп прироста:

; .

При прогнозировании объёмов продаж автомобилей (приведённый выше пример, таблица 6) получаем следующие варианты прогнозов:

Вариант А. ;.

Вариант Б. ;.

2.2.3. Аппроксимация динамического ряда аналитическими функциями

При аппроксимации динамического ряда известными аналитическими функциями предполагается, что для прогнозирования будет использована функция, у которой форма кривой ближе всего подходит к графическому тренду. Самый простой способ выбора функции – визуальный, на основе графического изображения динамического ряда. Чаще всего для аппроксимации используются:

• линейная функция ;

• парабола ;

• гипербола ;

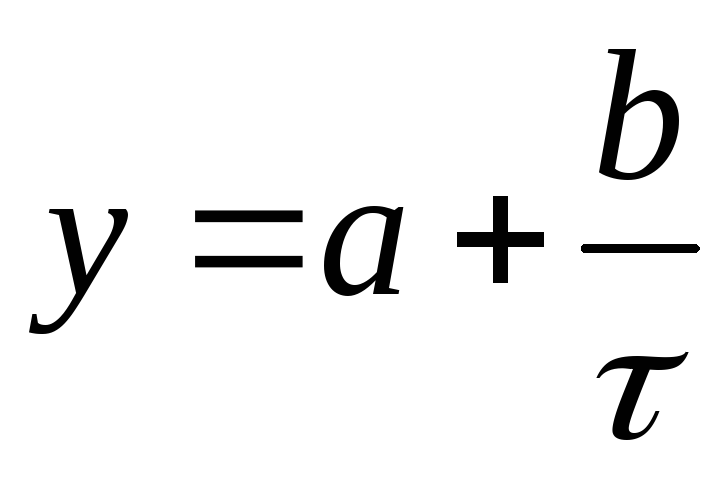• логарифмическая функция ;

• экспоненциальная функция ;

• степенная функция .

• показательная .

Каждая функция имеет свою сферу применения. Например, линейная функция используется для описания равномерно развивающихся процессов, а гипербола хорошо описывает процессы, для которых характерно насыщение рынка.

Для определения значений эмпирических коэффициентов иобычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:

,

где и- расчетные и фактические значения;

- число наблюдений.

Так для линейной функции имеем:

Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдем неизвестные эмпирические коэффициенты:

или

При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:

,

где - коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 7);

- среднее квадратическое отклонение от тренда,

;

- число параметров аналитической зависимости.

Таблица 7

Значения коэффициента доверия по распределению Стьюдента

Уровень доверительной вероятности,	0,683	0,95	0,99	0,997
Коэффициент доверия,	1	1,96	2,576	3

Пример. Используя данные задачи из параграфа 2.2.1. составить прогноз объёмов продаж автомобилей на 2006 год используя линейную и параболическую функции.

Решение:

Результаты предварительных расчётов сведём в таблицу 8.

Таблица 8