Вычисление равновесия

Рассмотрим модель с двумя фирмами (дуополию). Для определения равновесной цены вычислим наилучшие ответы каждой из фирм.

Прибыль i-й фирмы имеет вид:

.

Ее наилучшим ответом является объем выпуска , максимизирующий прибыльпри заданном объеме выпуска другой фирмы. Производнаяпо переменнойимеет вид:

Приравнивая ее к нулю, получим:

Значения , удовлетворяющие данному условию, являются наилучшими ответами фирмыi. Равновесие в данной модели достигается, еслиявляется наилучшим ответом на, а- наилучшим ответом на.

Пример

Пусть обратная функция спроса имеет вид: , а издержки фирмыiтаковы, что,. Тогда прибыль фирмыiсоставит:

Решение задачи максимизации имеет вид:

Таким образом, задача фирмы 1:

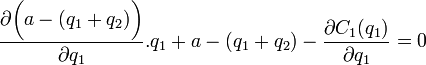
Из симметрии рассматриваемой системы:

Полученные выражения представляют собой функции наилучших ответов. В равновесии Нэша обе фирмы будут придерживаться стратегий, являющихся решениями пары этих уравнений. Подставляя в наилучший ответ фирмы 1, получим:

Равновесием Нэша в этой системе являются объемы выпуска , а равновесная рыночная цена будет представлять собой величину.

Модель Штакельберга

Материал из Википедии — свободной энциклопедии

Перейти к: навигация,поиск

Содержание 1 Общая характеристика 2 Основные предпосылки 3 Частный случай: моделирование дуополии 4 Сравнение выводов с выводами модели Курно 5 См. также 6 Ссылки

Общая характеристика

Модель Штакельберга—теоретико-игроваямодельолигополистического рынкапри наличии информационной асимметрии. Названа в честь немецкого экономистаГенриха фон Штакельберга, впервые описавшего ее в работеMarktform und Gleichgewicht(Структура рынка и равновесие), вышедшей в 1934 г.

В этой модели поведение фирм описывается динамической игрой с полной совершенной информацией, что отличает её от модели Курно, в которой поведение фирм моделируется с помощьюстатическойигры с полной информацией. Главной особенностью игры является наличие лидирующей фирмы, которая первой устанавливает объём выпуска товаров, а остальные фирмы ориентируются в своих расчетах на нее.

Основные предпосылки

1. Отрасль производит однородный товар: отличия продукции разных фирм пренебрежимо малы, а значит, покупатель при выборе, у какой фирмы покупать, ориентируется только на цену

2. Фирмы устанавливают количество производимой продукции, а цена на неё определяется исходя из спроса.

3. Существует так называемая фирма-лидер, на объём производства которой ориентируются остальные фирмы.

Частный случай: моделирование дуополии

Пусть существует отрасль с двумя фирмами, одна из которых «фирма-лидер», другая — «фирма-последователь». Пусть цена на продукцию является линейной функцией общего объема предложения Q:

.

Предположим также, что издержки фирм на единицу продукции постоянны и равны с₁ис₂соответственно. Тогда прибыль первой фирмы будет определяться формулой

,

а прибыль второй соответственно

.

В соответствии с моделью Штакельберга, первая фирма — фирма-лидер — на первом шаге назначает свой выпуск Q₁. После этого вторая фирма — фирма-последователь — анализируя действия фирмы-лидера определяет свой выпускQ₂. Целью обеих фирм является максимизация своих платёжных функций.

Равновесие Нэшав этой игре определяется методом обратной индукции. Рассмотрим предпоследний этап игры — ход второй фирмы. На этом этапе фирма 2 знает объем оптимального выпуска продукции первой фирмойQ₁^*. Тогда задача определения оптимального выпускаQ₂^*сводится к решению задачи нахождения точки максимума платёжной функции второй фирмы. Максимизируя функцию Π₂по переменнойQ₂, считаяQ₁заданным, находим, что оптимальный выпуск второй фирмы

.

Это наилучший ответ фирмы-последователя на выбор фирмой-лидером выпуска Q₁^*. Фирма-лидер может максимизировать свою платёжную функцию, учитывая вид функцииQ₂^*. Точка максимума функции Π₁по переменнойQ₁при подстановкеQ₂^*будет

.

Подставляя это в выражение для Q₂^*, получим

.

Таким образом, в равновесии фирма-лидер производит в два раза большее количество продукции, нежели фирма-последователь.