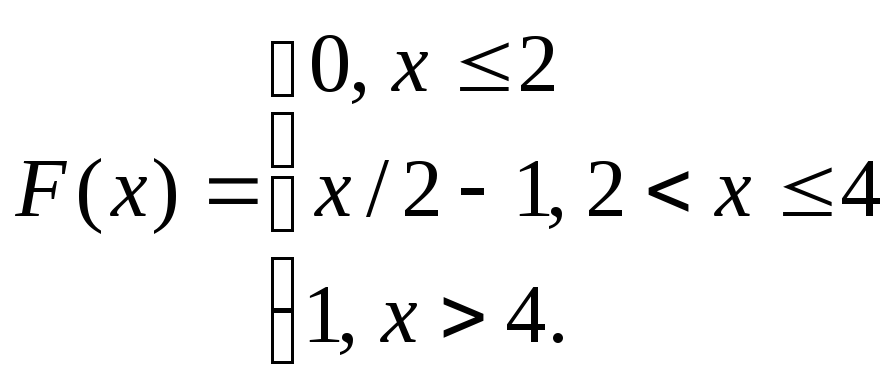1. Вероятность изделия отличного качества 0.9. Какова вероятность того, что из двух наудачу проверенных изделий только одно окажется отличного качества?

2. Из колоды в 36 карт вытаскивается две карты. Какова вероятность, что только одна из них будет пиковой масти?

3. Монету бросают дважды. Какова вероятность выпадения герба только один раз?

4. В первой урне 5 белых и 5 черных шаров, во второй – 6 белых и 4 черных шара. Из каждой урны вынуто по два шара. Найти вероятность того, что хотя бы из одной урны вынуто два черных шара.

5. В первой урне 5 белых и 5 черных шаров, во второй – 6 белых и 4 черных шара. Из каждой урны вынуто по два шара. Найти вероятность того, что хотя бы из одной вынуто два белых шара.

6. В первой урне 5 белых и 5 черных шаров, во второй – 6 белых и 4 черных шара. Из каждой урны вынуто по два шара. Найти вероятность того, что хотя бы из одной урны вынут один белый и один черный шар.

7. Два автобуса-экспресса выехали в аэропорт. Вероятность того, что первый автобус прибудет вовремя – 0.9, второй – 0.8. Какова вероятность, что только один автобус прибудет вовремя?

8. Покупатель приобрел два изделия. Вероятность того, что первое изделие бездефектно – 0.95, второе – 0.9. Какова вероятность, что из приобретенных изделий только одно бездефектно?

9. В первой корзине 5 синих и 4 черных мяча, во второй – 6 синих и 3 черных. Из каждой корзины выбрали по два мяча. Какова вероятность, что хотя бы из одной корзины выбрали два синих мяча?

10. В команде А 2 девушки и 8 юношей, в команде В – 3 девушки и 7 юношей. Из каждой команды выбрали по 2 участника. Какова вероятность, что хотя бы из одной команды выбрано 2 юноши?

II.

На складе хранятся N изделий завода 1, M изделий – завода 2, K изделий завода 3. Вероятность получения бездефектного изделия на первом заводе – 0.9, на втором – 0.8, на третьем – 0.7.

а) Найти вероятность того, что извлеченное наудачу изделие будет бездефектным.

б) Извлеченное наудачу изделие оказалось бездефектным. Какова вероятность, что оно изготовлено на заводе i?

Вариант	1	2	3	4	5	6	7	8	9	10
N	20	30	30	40	30	40	20	50	30	40
M	15	20	15	20	10	10	20	10	20	10
K	10	10	20	20	10	20	30	20	15	15
i	1	2	3	1	2	3	1	2	3	1

III.

1-3.Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка = 0.9, для второго= 0.8. Найти вероятность того, что привыстрелах стрелки одновременно попадут в мишень:

а) менее трех раз; б) не менее трех раз; с) хотя бы один раз; д) найти наивероятнейшее число парных попаданий при выстрелах.

1.

2.

3.

4-6.Проводится турнир изматчей между двумя командами. Вероятность выигрыша в одном матче для первой команды 0.6. Какова вероятность, что первая команда выиграет: а) менее трех раз; б) не менее трех раз; с) хотя бы один раз; д) найти наивероятнейшее число выигрышей каждой из команд.

4.

5.

6.

7-10. Два спортсмена выполняют побросков мяча по воротам. Вероятность попадания первого – 0.6, второго – 0.7. Какова вероятность, что оба попадут в ворота: а) более двух раз; б) не более двух раз; с) хотя бы один раз; д) найти наивероятнейшее число парных попаданий.

7.

8.

9.

11. 

IV.

При обследовании уставных фондов банков установлено, что n-я часть банков имеют уставной фонд свыше 100 млн. руб. Найти вероятность того, что среди 500 банков имеют уставной фонд свыше 100 млн. руб.: a) не менее m; b) от m до k включительно.

В-т	1	2	3	4	5	6	7	8	9	10
n	4	5	6	4	5	6	4	5	6	4
m	200	300	100	300	200	250	150	100	300	250
k	300	400	200	400	300	350	250	250	400	350

V.

В ящике содержится n деталей, среди которых k бракованных. Сборщик наудачу извлекает m деталей.

1. Найти вероятность того, что среди извлеченных деталей: a) m бракованных; b) одна бракованная; c) две бракованные; d) хотя бы одна бракованная.

2. Составить закон распределения случайной величины X– числа бракованных деталей среди извлеченных.

3. Найти M(X), D(X), .

4. Вычислить P(1<X<4)

В-т	1	2	3	4	5	6	7	8	9	10
n	10	12	11	11	10	12	11	12	12	10
k	4	5	4	5	3	4	5	5	6	5
m	3	4	3	3	3	3	4	3	3	4

VI.

Непрерывная случайная величина X задана функцией распределения F(x). Найти плотность распределения f(x), математическое ожидание и дисперсию случайной величины. Изобразить графики функции распределения F(x) и плотности распределения f(x). Найти вероятность попадания случайной величины в интервал

1.	2.

VII.

Известны математическое ожидание a и среднее квадратичное отклонение нормально распределенной случайной величиныX. Найти: a) вероятность попадания этой величины в заданный интервал ;b) вероятность того, что абсолютная величина X-a отклонения окажется меньше c) вычислить M(3X-2), D(3X-2).

вариант	1	2	3	4	5	6	7	8	9	10
	10	9	8	7	6	5	4	3	2	2
	4	5	1	2	3	1	5	2	5	4
	2	5	4	3	2	1	2	3	4	6
	13	14	9	10	11	12	11	10	9	10
	3	4	2	1	2	2	3	1	2	3