
mat
.pdf
• Уравнение прямой с угловым коэффициентом k:
y = kx+b.
Если известны координаты двух различных точек А(хA;уA) и В(хB;уB) на прямой, то угловой коэффициент можно вычислить по формуле
k= уB − уA . хB − хA
•Уравнение прямой с заданным угловым коэффициентом k и
проходящей через точку (x0;y0):
y − y0 = k(x − x0 ).
Если в этом уравнении менять k, то получим семейство прямых, проходящих через точку (x0;y0), которое называют «пучком прямых».
• Уравнение прямой, проходящей через две заданные точки
А(хA;уA) и В(хB;уB):
x − xA |
= |
y − yA |
. |
|
|
||
xB − xA |
yB − yA |
||
Если xB = xA , топрямаяпараллельнаосиOy, еёуравнение: x = xA. Если yB = yA , топрямаяпараллельнаосиOx, еёуравнение: y = yA.
3. Взаимное расположение прямых.
Пусть k1 и k2 – угловые коэффициенты двух прямых.
•Условие параллельности прямых: k1 = k2 .
•Условие перпендикулярности прямых: k1 k2 = −1.
4. Положение точки относительно прямой.
Формула нахождения расстояния от точки М(x0;y0) до прямой
Ax + By + C = 0:
d = Ax0 + By0 +C . A2 + B2
Точка М(x0;y0) лежит на прямой Ax + By + C = 0 тогда и только тогда, когда ее координаты удовлетворяют уравнению прямой, то есть справедливо равенство Ax0 + By0 + C = 0. Очевидно, что в этом случае d = 0.
21
Задача. Рассмотрим решение задачи, аналогичной задачам 1-10,
если даны точки А(2;1), В(–4;4), С(–1,5).
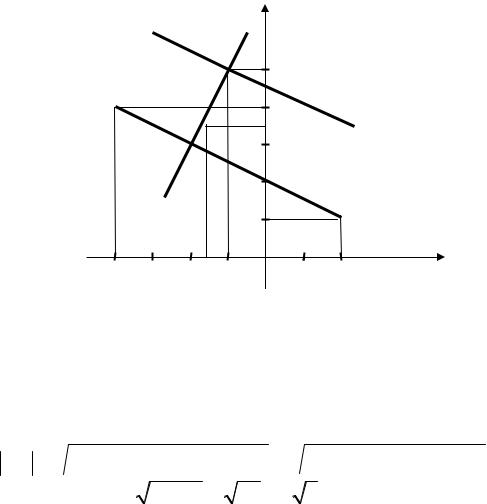
Решение. Начнем решение задачи с выполнения чертежа (рис. 1). Построим точки А(2;1), В(–4;4), С(–1;5) в прямоугольной системе координат Oxy. Проведем прямую АВ, уравнение которой необходимо найти, а затем через точку С проведем прямую СК параллельно АВ и прямую СD перпендикулярно АВ.
y
B
C 5
4 K
3
D
2
A
1
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
x |
Рис. 1
1. Длину отрезка АВ находим как расстояние между двумя точками
А(2;1) и В(–4;4):
AB = 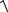 (xB − xA )2 + (yB − yA )2 =
(xB − xA )2 + (yB − yA )2 = 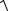 (− 4 − 2)2 + (4 −1)2 =
(− 4 − 2)2 + (4 −1)2 =
= 36 +9 = 45 = 3 5 ≈ 6,7.
2. Уравнение прямой АВ найдем по формуле уравнения прямой, |
||||
проходящей через две заданные точки А(хA;уA) и В(хB;уB) : |
||||
|
x − xA |
= |
y − yA |
, |
|
|
|
||
|
xB − xA |
yB − yA |
||
в нашем случае:
22
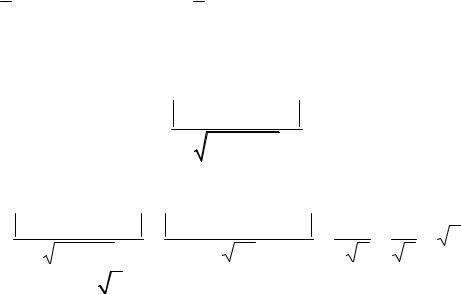
x − 2 |
= |
y −1 |
, то есть |
x −2 |
= |
y −1 |
. |
||
−4 − 2 |
4 −1 |
|
−6 |
3 |
|
||||
Запишем пропорцию: 3×(х – 2) = – 6×(у – 1), раскроем скобки и перенесём все слагаемые в левую часть уравнения, получим окончательный ответ 3х + 6у – 12 = 0 − уравнение прямой АВ.
3. Найдем угловой коэффициент прямой АВ:
|
|
|
kAB = |
уB − уA |
= |
4 −1 |
= |
3 |
= − |
1 |
, |
|
|
|||
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
хB − хA |
−4 −2 |
−6 |
|
|
|
|||||
по условию перпендикулярности прямых СD и АВ: |
kCD kAB = −1. |
|||||||||||||||
Тогда |
k |
= − |
1 |
= − |
|
1 |
= 2. Уравнение прямой СD запишем в |
|||||||||
|
|
|
||||||||||||||
|
CD |
|
kAB |
−1/ 2 |
|
|
|
|
|
|
|
|
|
|
||
виде уравнения пучка прямых, проходящих через точку С: |
||||||||||||||||
|
|
|
|
|
|
y − yC = k(x − xC ) . |
|
|
|
|
||||||
Подставив в уравнение координаты точки С(– 1, 5) |
и значение |
|||||||||||||||
k = kCD = 2, |
получим |
у –5=2(х+1); |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
у –5=2х+2; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
2х – у+7=0 – уравнение прямой СD. |
||||||||||
4. По условию параллельности прямых СЕ и АВ: |
kCE |
= kAB = − 1 . |
||||||||||||||
Уравнение прямой СЕ |
|
|
|
|
|
|
|
|
|
|
2 |
|||||
запишем в виде уравнения пучка прямых, |
||||||||||||||||
проходящих через точку С: |
y − yC = k(x − xC ) . |
|
|
|
|
|||||||||||
Подставив в уравнение координаты точки С(– |
1, |
5) |
и значение |
|||||||||||||
k = kCE = −12 , получим у –5=−12 (х+1);
у –5=−0,5х−0,5; 0,5х + у−4,5=0 – уравнение прямой СЕ.
5. Расстояние от точки С до прямой АВ найдём по формуле
d = Ax0 + By0 +C . A2 + B2
Уравнение прямой АВ найдено ранее (см. пункт 2): 3х + 6у – 12 = 0.
Тогда |
d = |
3xC + 6 yC −12 |
= |
3 (−1) + 6 5 −12 |
= |
15 |
= |
5 |
= 5 |
≈ 2,24 . |
|||||
32 + 62 |
45 |
3 5 |
5 |
||||||||||||
|
|
|
|
|
|
|
|||||||||
Ответы. |
1) |
|
АВ |
|
=5 3 ≈ 6,7; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
2) 3х + 6у – 12 = 0 − уравнение прямой АВ;
23
3)2х – у+7=0 – уравнение прямой СD;
4)0,5х + у−4,5=0 – уравнение прямой СЕ;
5)d =  5 ≈ 2,24 .
5 ≈ 2,24 .
Введение в математический анализ
Задачи 11–20
Вычислить пределы функции y=f(x), при указанном поведении аргумента x.
11. |
f (x) = |
x2 |
− x −2 |
|
; |
|
|
|
|
|
|
|
|
|||||||
x |
2 −5x +6 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
а) x →1; |
|
б ) x → 2; |
в) x → −1; |
г) x → 3; |
д) x → ∞. |
||||||||||||||
12. |
f (x) = |
x2 +3x + |
2 |
|
; |
|
|
|
|
|
|
|
|
|||||||
2x2 + x − |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
а) x → −2 ; |
б ) x → 0,5 ; |
в) x → −1; |
г) x → 3; |
д) x → ∞. |
|||||||||||||||
13. |
f (x) = |
|
|
2x2 |
− |
3x −9 |
; |
|
|
|
|
|
|
|
||||||
|
|
x2 |
−2x −3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
а) x →1; |
|
б) |
|
x → −1,5; в) x → −1; г) x → 3; |
д) x → ∞. |
||||||||||||||
14. |
f (x) = |
|
3x2 |
− |
5x − |
2 |
; |
|
|
|
|
|
|
|
||||||
|
|
x |
2 −2x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
а) x → 5; |
|
б) x → 2; |
в) x → − |
; |
г) x → 0 ; д) x → ∞. |
||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
15. |
f (x) = |
|
|
−4x −5 |
; |
|
|
|
|
|
|
|
||||||||
|
2x2 |
− |
9x −5 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
а) x → 5; |
|
б) x → 2; |
в) x → −1; |
г) x → −0,5 ; |
д) x → ∞. |
||||||||||||||
16. |
f (x) = |
|
|
|
4x2 − x |
|
|
|
|
; |
|
|
|
|
|
|
|
|||
|
4x2 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3x −1 |
|
|
|
|
|
1 |
|
|
||||||||
|
а) x →1; |
б) x → 0 ; |
в) x → −1; |
г) x → |
; д) x → ∞. |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
17. |
f (x) = |
|
|
2x2 |
+ |
3x −5 |
; |
|
|
|
|
|
|
|
||||||
|
x2 + 4x −5 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
а) x →1; |
б) x → −5 ; |
в) x → − |
5 |
|
; |
г) x → 3; д) x → ∞. |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
18. |
f (x) = |
5x2 |
−12x + |
4 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 |
+ x −6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а) x → −3; |
б) x → 2; |
в) x → −1; |
|
г) x → |
; д) x → ∞. |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
19. |
f (x) = |
|
x2 |
−2x −3 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3x2 |
−13x + |
12 |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
а) x → −1; |
б) x → |
; |
в) x →1; |
|
г) x → 3; |
д) x → ∞. |
||||||||||||||
|
3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
f (x) = |
x2 + x −12 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+ x −28 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|||||
|
а) x → −4 ; б) x → 2; |
в) x → |
; |
|
г) x → 3; |
д) x → ∞. |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
Методические указания к решению задач 11 – 20
Пределы функций, основные теоремы о пределах
1. Предел функции. Предел функции f(х) - это число А, к которому неограниченно приближаются значения функции при указанном
стремлении аргумента х. |
|
2. Теоремы о пределах. |
|
Пусть существуют конечные пределы |
lim f (x) = A и |
|
x→x0 |
lim g(x) = B . Тогда справедливы следующие утверждения:
x→x0
•lim ( f (x) ± g(x)) = lim f (x) ± lim g(x) = A ± B ;
→x0 x→x0 x→x0
• |
lim ( f (x) g(x)) = lim |
f (x) lim |
g(x) = A B ; |
|
|
x→x0 |
x→x0 |
x→x0 |
|
• |
lim c f (x) = c |
lim f (x) = cA , |
где с – число; |
|
|
x→x0 |
x→x0 |
|
|
25
|
f (x) |
|
lim f (x) |
|
A |
|
|
|
• lim |
= |
x→x0 |
= |
, если |
lim g(x) ≠ 0 . |
|||
g(x) |
lim g(x) |
B |
||||||
x→x0 |
|
|
|
x→x0 |
||||
|
|
|
x→x0 |
|
|
|
|
3. Бесконечно малые и бесконечно большие функции. Бесконечно малой функцией при x → x0 называется функция α(x),
предел которой равен нулю при x → x0 : limα(x) = 0 .
x→x0
Если значения функции f(x) неограниченно возрастают по абсолютной величине при x → x0 , то такую функцию называют беско-
нечно большой при x → x0 . Предел этой функции обозначают зна-
ком бесконечности ∞: lim f (x) = ∞ (±∞).
x→x0
Теоремы о связи бесконечно малых и бесконечно больших функций.
Если |
lim α(x) = 0 , то |
lim |
1 |
|
=∞. |
||
α(x) |
|||||||
|
x→x0 |
x→x0 |
|
||||
Если |
lim f (x) = ∞, то |
lim |
1 |
|
= 0. |
||
|
f (x) |
||||||
|
x→x0 |
x→x0 |
|
|
|||
Утверждения всех вышеприведённых теорем также справедливы, если х → ∞ (+∞ или −∞).
Задача. |
Вычислить пределы функции |
f (x) = |
3x2 |
+10x −8 |
при |
||||||
4x2 |
+15x −4 |
||||||||||
|
|
|
|
|
|
|
|
||||
a) x →1; |
б) x → −4; |
в) x → |
1 |
; |
г) x → |
|
2 |
; |
д) x → ∞. |
||
4 |
|
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|||
Решение. В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента х.
а) |
lim |
3x2 +10x −8 |
= |
3 12 +10 1−8 |
= |
|
5 |
= |
1 |
. |
|||
|
|
|
|
|
|||||||||
|
x→1 4x2 +15x −4 4 12 +15 1−4 |
15 3 |
|
||||||||||
б) |
lim |
|
3x2 |
+10x −8 |
. |
|
|
|
|
|
|
|
|
|
|
+15x −4 |
|
|
|
|
|
|
|
||||
|
x→−4 4x 2 |
|
|
|
|
|
|
|
|
||||
При подстановке x = −4 в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пре-
26
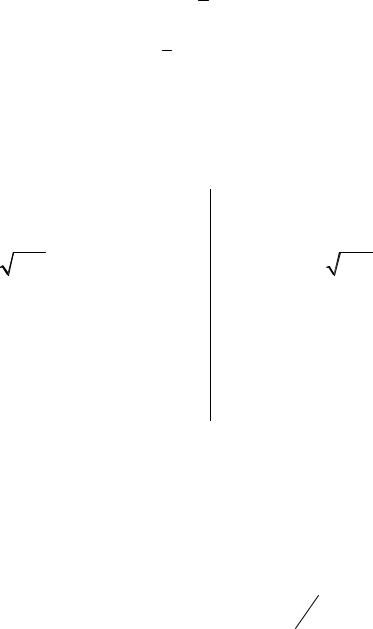
деле частного здесь не применима. В данном случае говорят, что
имеется неопределенность вида 0 .
0
Неопределенность вида 0 при x → x0 может быть раскрыта
0
сокращением дроби на множитель вида (х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на (х+4).
Поэтому следует разложить на множители числитель и знаменатель дроби.
3х2+10х – 8 = 0;
D = 102 −4 3 (−8) =196;
x |
|
= |
−10 ± |
196 |
= |
−10 ±14 |
; |
||
|
|
|
|
|
|
||||
1,2 |
|
2 3 |
6 |
|
|||||
|
|
|
|
||||||
x |
= −4; x |
= |
2 |
. |
|
|
|
||
|
|
|
|
||||||
1 |
|
2 |
3 |
|
|
|
|
||
3х2+10х–8 = 3(х+4)(х–2/3) = = (х+4)(3х–2).
Таким образом,
4х2+15х– 4 = 0;
D = 152 − 4 4 (−4) = 289;
x |
|
= |
−15 ± |
289 |
= |
−15 ±17 |
; |
|||
|
|
|
|
|||||||
1,2 |
2 |
4 |
8 |
|
||||||
|
|
|
||||||||
x |
= −4; |
x |
= |
1 |
. |
|
|
|||
|
||||||||||
1 |
|
|
|
2 |
4 |
|
|
|
|
|
4х2+15х – 4 = 4(х+4)(х–1/4 ) = = (х+4)(4х–1).
|
|
|
|
3x2 |
+10x −8 |
|
|
|
0 |
|
|
|
|
|
|
(x + 4)(3x −2) |
|
|
3x −2 |
|
−14 |
|
14 |
|
||||||||||||||||
lim |
|
|
|
|
|
|
|
= |
|
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
= lim |
|
= |
|
= |
|
|
. |
||||||||||
|
|
|
+15x −4 |
|
|
|
|
|
|
|
|
|
|
|
4x −1 |
−17 |
17 |
|||||||||||||||||||||||
x→−4 4x4 |
|
|
|
0 |
|
x→−4 (x + 4)(4x −1) |
x→−4 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
2 |
2 |
+10 |
2 |
−8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3x |
+10x |
−8 |
|
|
3 |
|
|
|
3 |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
в) |
lim |
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
= 0. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
|
|
70 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
2 4x2 +15x −4 |
4 |
|
+15 |
−4 |
|
9 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x→3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь применима теорема о пределе частного, так как предел |
|
|
|
|||||||||||||||||||||||||||||||||||||
знаменателя существует и не равен нулю. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
3x2 |
+10x −8 |
|
|
3 |
|
1 |
|
+10 |
1 |
|
−8 |
− 85 |
/ 16 |
|
|
|
|
|
|
|
|
|
|||||||||||||
г) |
lim |
|
|
|
16 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= ∞. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x→ |
1 |
|
|
4x2 |
+15x − 4 |
|
|
4 |
|
+15 |
|
|
− 4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
16 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.
27

д) lim 3x2 +10x −8 . x→∞ 4x2 +15x −4
Пределы числителя и знаменателя дроби равны ∞. В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
Чтобы раскрыть неопределенность вида |
|
∞ |
при |
x → ∞, |
|
|
|||
|
|
∞ |
|
|
каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
|
|
|
|
|
|
|
|
|
|
|
3x2 |
10x |
|
|
|
8 |
|
|
|
|
|
|
10 |
8 |
|
|
|
|
|||||||||||
|
3x2 |
+10x −8 |
|
∞ |
|
|
|
|
|
|
2 |
|
+ |
2 |
|
|
− |
|
|
|
|
|
|
3 + |
|
x |
− |
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
x |
|
|
x |
2 |
|
|
|
|
|
x |
2 |
|
|
|
|||||||||||||||||||
lim |
|
|
|
|
= |
= |
lim |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= |
|
, |
|||||
|
|
|
|
|
|
4 15x |
|
|
|
|
|
4 |
|
|
|
|
|
|
15 4 |
|
4 |
||||||||||||||||||
x→∞ 4x2 +15x −4 |
|
∞ |
x→∞ |
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x2 |
|
|
− |
|
|
|
|
|
|
4 + |
|
x |
− |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
x2 |
|
|
|
x2 |
|
|
|
|
|||||||||||||||
так как |
lim |
10 |
|
= 0; lim |
8 |
|
= 0; |
|
lim |
15 |
|
= 0; |
|
lim |
4 |
= 0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x→∞ x |
|
x→∞ x2 |
|
|
|
|
|
x→∞ x |
|
|
|
|
|
x→∞ x2 |
|
|
|
|
|
|
|
|
|||||||||||||||
(потеореме освязибесконечнобольшойибесконечномалойфункций).
Ответы. а) |
1 |
; |
б) |
14 |
; в) 0; |
г) ∞; |
д) |
3 |
. |
||
3 |
|||||||||||
|
|
|
|||||||||
17 |
4 |
||||||||||
|
|
|
|
|
|
|
|||||
Дифференциальное исчисление функции одной переменной
Задачи 21–30
Найти производные данных функций и их дифференциалы.
31. а) |
y = 3x |
4 |
5 |
+ 2 ; |
|
|
|
2x2 |
|
||
|
− |
|
|
б) |
y = |
|
; |
|
|||
|
4 x |
|
|
||||||||
|
|
1−3x |
|
||||||||
в) |
y = 2cos x ln x + |
1−4x2 . |
|
|
|
|
|
||||
32. a) |
у = 5х2 +43 x5 +3; |
б) |
y = |
x3 −2x |
; |
||||||
в) |
y = arctg x4 − x ln x . |
3x |
|||||||||
|
|
|
|
|
|||||||
28
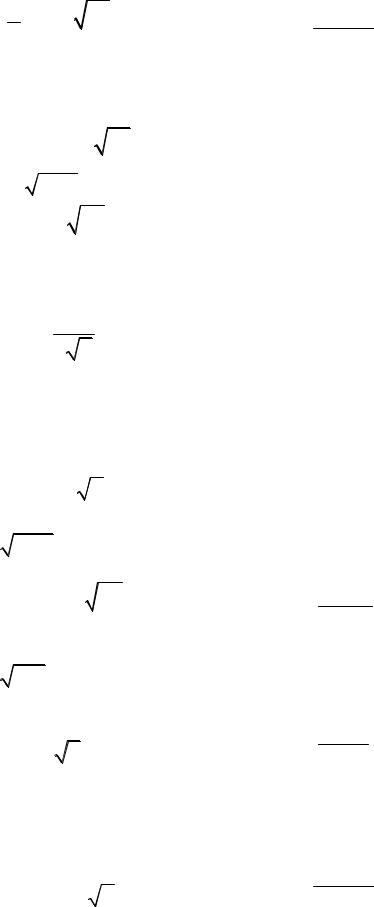
33.а) y = 14 x8 +88 x3 −1; в) y = cos(ln x) + x2 tg x .
34. |
а) |
y = |
1 |
x5 −3x 3 x −4 ; |
|
||||
|
|
5 |
|
|
|
в) |
y = ln x −1 + x3 arctg x . |
||
35. |
а) |
y =3x8 +55 x2 −3; |
||
в) y = tg ex +sin x ln x .
36.а) y = 5x4 − x 2 x +3;
в) y = ln(sin x) − x6 tg x .
37. |
а) |
y = 4x3 + |
3 |
−2; |
|
||||
|
|
|
x 3 x |
|
|
в) |
y = sin x − x ctg x. |
||
38. |
а) |
y = 7x5 −3x 3 x2 −6; |
||
в) y = ln x −(1−2x2 ) sin x .
39. а) y = 3x4 − |
4 |
−3; |
|
||
|
4 x |
|
в) y = tg x2 +sin x ex .
40. а) |
y =8x2 − |
9 |
|
+6; |
|
|
|||
|
x2 |
x |
||
в) |
y = arcsin x3 +ln x cos x . |
|||
б) y = 4x2 −1 ; 1− x2
б) |
y = |
x +3 |
; |
||||||
2x −5 |
|||||||||
|
|
|
|
|
|||||
б) |
y = |
|
3x4 |
|
; |
|
|||
|
x −3 |
|
|||||||
|
|
|
|
|
|
|
|||
б) |
y = |
2x −1 |
|
; |
|||||
|
|||||||||
|
|
|
|
x5 |
|
|
|
||
б) |
y = |
1−6x2 |
; |
||
1 |
+ x |
||||
|
|
|
|||
б) y = 2x + 4 ;
1+ x2
б) y = x6 −1; 2x +1
б) y = 2x2 −1 ; x2 +1
29
Методические указания к решению задач 21 – 30
Производная и дифференциал функции одной переменной
1. Понятие производной. Производной для функции у = f(х) в точке х0 называется предел отношения приращения функции у к приращению аргумента х, при условии, что приращение аргумента стремится к нулю и указанный предел существует:
|
y |
|
|
f(x) − f(x0 |
) |
|
′ |
|
lim |
|
= |
lim |
|
|
= |
f (x0 |
) |
x |
x − x0 |
|
||||||
x→0 |
|
x→x0 |
|
|
|
|
Производная f’(х0) показывает скорость изменения функции f(х) в точке х0. Геометрически f’(х0) = tgα, где α – угол наклона касательной, проведенной к графику функции f(х) в точке х0. Нахождение производной для функции f(х) называется её дифференцированием.
2. Дифференциал функции.
Дифференциал функции равен произведению производной этой
функции на дифференциал независимой переменной dx = х: dy = f ′(x)dx.
3. Правила дифференцирования. Пусть даны дифференцируемые функции u(x) и v (x), тогда справедливы формулы:
′ |
= u |
′ |
′ |
(u +v) |
|
+v ; |
(u −v)′ = u′−v′;
(u v)′ = u′ v +u v′;
u ′ |
u′ v −u v′ |
|
|||
|
|
|
= |
|
. |
|
v2 |
||||
v |
|
|
|||
Отметим также, что:
а) производная от независимой переменной равна единице: x′ =1; б) производная постоянной величины с равна нулю: c′ = 0;
в) постоянный множитель выносится за знак производной: (cu)′ = c u′.
30
