Тема 3. Прогнозирование на основе многофакторных регрессионных моделей

3.1. Задания к практическим занятиям

Задание 3.1.На основе данных за 1-12 периоды:

1. рассчитать параметры уравнения линейной многофакторной регрессии;

2. оценить качество полученной модели.

Задание 3.2.На основе полученных данных выполнить прогноз на 13-18-ый месяцы, определив доверительный интервал прогноза для уровня значимости=0,05. Рассчитать ошибку прогноза.

Представить результаты в форме табл. 4. Сделать выводы.

3.2. Методические указания к практическим занятиям

Оценка параметров уравнения многофакторной регрессии и его построение.

1. Оценка параметров уравнения линейной многофакторной регрессии.

Если между изучаемыми показателями обнаружена линейная зависимость, то уравнение многофакторной регрессии примет вид:

= a + b₁*x₁+ b₂*x₂ + b₃*x₃+ b₄*x₄+ b₅*x₅

Для оценки параметров уравнения линейной многофакторной регрессии необходимо на вкладке Данные вызвать Анализ данных →Регрессия.

В случае отсутствия на вкладке Данные кнопки Анализ данных необходимо выполнить следующую процедуру: зайти в меню «Файл»  «Параметры»  «Надстройки» далее выбрать «Пакет анализа» нажать кнопку «Перейти». После этого появится диалоговое окно, в котором необходимо поставить галочку напротив «Пакета анализа», а затем нажать ОК.

В раскрывшемся диалоговом окне Регрессия ввести только следующие данные (рис. 1):

1. «Входной интервал Y» - выделить весь диапазон числовых значений результативного показателя «Y» с 1 по 36 периоды;

2. «Входной интервал Х» - выделить весь диапазон числовых значений пяти факторных показателей «Х_i» с 1 по 36 периоды;

3. «Выходной интервал» - выделить одну пустую ячейку слева под таблицей исходных данных.

Рис. 1. Диалоговое окно ввода параметров инструмента Регрессия

После нажатия кнопки «ОК» в диалоговом окне Регрессии под таблицей исходных данных появятся результаты регрессионного анализа, которые называются «Вывод итогов» (рис. 2), который содержит три таблицы, в каждой из которых необходимо выделить заливкой и подписать:

1. Показатели таблицы «Регрессионная статистика»:

• множественный R – коэффициент корреляции R;

• R–квадрат – коэффициент детерминации R²;

• наблюдения – число исходных наблюдений.

2. Показатели таблицы «Дисперсионный анализ»:

• столбец «F» – расчетное (фактическое) значение F-критерия Фишера F_факт.

3. Показатели таблицы 3:

• ячейка на пересечении столбца «Коэффициенты» и строки «Y - пересечение» – значение параметра уравнения регрессии а - «отрезок».

• ячейки на пересечении столбца «Коэффициенты» и строк «Переменные Х₁, Х₂, Х₃, Х₄, Х₅» - значения параметров уравнения регрессии b₁, b₂, b₃, b₄, b₅ – «наклон».

Рис. 2. Результат применения инструмента Регрессия

2. Построение уравнения многофакторной регрессии.

Для построения полученного уравнения регрессии необходимо в табл. 3 рассчитать значение по формуле:

= абсолютный адрес коэффициента (а) + абсолютный адрес коэффициента (в₁) * относительный адрес значения x₁ + абсолютный адрес коэффициента (в₂)* относительный адрес значения x₂ + абсолютный адрес коэффициента (в₃)* относительный адрес значения x₃ + абсолютный адрес коэффициента (в₄)* относительный адрес значения x₄ + абсолютный адрес коэффициента (в₅)* относительный адрес значения x₅.

Абсолютный адрес означает, что в адрес ячейки вводится символ доллара (например, $E$5). Для этого достаточно нажать клавишу F4, после введения в строку формул адреса соответствующей ячейки (адрес ячейки «коэффициент (в)»  F4).

Таблица 3

Таблица вспомогательных расчетов многофакторной регрессии

Месяц	Значение факторных показателей					Фактические значения результативного показателя, Yф	Теоретические значения результативного показателя, (Yт)			(Yф - Yт)2
	Х1	Х2	Х3	Х4	Х5
1
2
…
11
12
Итого	-	-	-	-	-			-		

После ввода формулы нажать клавишу Enter и захватив мышью правый нижний угол ячейки, протянуть ее на нужное количество строчек вниз.

Оценка качества построенного уравнения многофакторной регрессии.

Качество любого уравнения регрессии оценивается по трем параметрам:

1. Коэффициент детерминации (R²) – результат операции Регрессия - таблица «Регрессионная статистика» (R–квадрат);

2. Критерий Фишера – необходимо знать F_факт (результат операции Регрессия - столбец «F») и F_табл (определяется по таблице, приложение 3);

3. Средняя ошибка аппроксимации (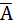), которая определяется по формуле:

Для нахождения средней ошибки аппроксимации необходимо в табл. 3 рассчитать две колонки:

• ;

• - для нахождения используем математическую функцию ABS.

Качество построенной регрессионной модели считается высоким если:

1. Коэффициент детерминации (R²) больше либо равен 0,5;

2. Критерий Фишера F_табл < F_факт;

3. Средняя ошибка аппроксимации () меньше либо равна 10 %.

Если все три условия выполняются, то построенная модель может быть использована для прогнозирования. Если хотя бы одно из условий не выполняется, то модель низкого качества и не может быть использована для прогнозирования.

Прогноз результативного показателя «Y» на 13-18-ый месяцы по полученному уравнению многофакторной регрессии.

Для расчета прогнозного значения результативного показателя Y на 13-18-ый месяцы необходимо:

1. поставить курсор в ячейку, находящуюся на пересечении строки «13» и столбца «Прогнозное значение показателя» табл. 4;

2. ввести формулу: = абсолютный адрес коэффициента (а) + абсолютный адрес коэффициента (b₁) * относительный адрес значения x₁ в январе прогнозируемого года + абсолютный адрес коэффициента (b₂)* относительный адрес значения x₂ в январе прогнозируемого года + абсолютный адрес коэффициента (b₃)* относительный адрес значения x₃ в январе прогнозируемого года + абсолютный адрес коэффициента (b₄)* относительный адрес значения x₄ в январе прогнозируемого года + абсолютный адрес коэффициента (b₅)* относительный адрес значения x₅ в январе прогнозируемого года.

3. после ввода формулы нажать клавишу Enter и захватив мышью правый нижний угол ячейки, протянуть ее на 6 месяцев прогнозируемого периода.

4. в строке «Итого» рассчитать суммарное значение прогнозируемого показателя за год.

5. рассчитать ошибку прогноза по формуле:

Таблица 4

Результаты прогнозирования на основе многофакторных моделей на 13-18 мес.

Месяцы	Значение показателя Х1	Значение показателя Х2	Значение показателя Х3	Значение показателя Х4	Значение показателя Х5	Фактическое значение результативного показателя, Yф	Прогнозное значение результативного показателя, YПР	Ошибка прогноза, %	Доверительный интервал прогноза (α = 0,05)
									Верхняя доверительная граница	Нижняя доверительная граница
1	2	3	4	5	6	7	8	9	12	13
13 14 15 16 17 18								= (гр.8- гр.2) / гр.2*100
За полугодие									-	-
							а = b1 = b2 = b3 = b4 = b5 =	… … … … … …

Для этого:

• поставить курсор в ячейку, находящуюся на пересечении столбца «Ошибка прогноза» и строки «Январь»;

• ввести формулу расчета ошибки прогноза;

• после ввода формулы нажать клавишу Enter и, захватив мышью правый нижний угол ячейки, протянуть ее на всю колонку, включая строку «Итого».

При составлении прогнозов уровней социально-экономических явлений обычно используют интервальные оценки, рассчитывая доверительные интервалы прогноза.

Границы интервалов определяются по формуле:

где Y_Т - точечный прогноз, расчитанный по линейной модели,

t_a - коэффициент доверия по распределению Стьюдента при уровне значимости  = 0,05 (см. Приложение 4);

S_y – стандартная ошибка аппроксимации,

(расчет в табл. 3);

n – число уровней ряда (в данном случае n=12);

l – число параметров в уравнении регрессии (для пятифакторной линейной регрессии прямой l=6).