Лекция №6
Ортогональные преобразования сигналов в базисе функций Уолша
Непрерывные функции Уолша относятся к классу кусочно-постоянных знакопеременных функций, задаваемых на отрезке 0, 1 либо 1
2, 1
2 и принимающих значения 1 . Для представления реальных, ограниченных во времени сигналов с началом отсчета в нулевой точке, удобно пользоваться функциями Уолша с интервалом определения 0, 1 .
.
Базис функций Уолша
• Интервал определения функций Уолша можно представить как совокупность N 2mравных(m 1,2,...) подынтервалов, на каждом из которых функции Уолша принимают значения +1 или -1, а на концах подынтервалов имеют разрывы первого рода, причем в этих точках функции Уолша непрерывны справа.
•Совместно записанные и пронумерованные функции Уолша образуют базисную систему, в которой можно разложить произвольный сигнал в ряд Уолша. Поскольку нумерация (упорядочение) функций Уолша может быть выполнена различными способами, то возможны три варианта упорядочения: по Пэли, Хармуту и Адамару.
Функции Радемахера
•Каждая из систем упорядочения функций Уолша может
быть построена и аналитически описана с помощью кусочно-постоянных функций Радемахера r(k,t) . Эти функции на интервале 0, 1 заданы следующим образом:
r(0,1) 1; r(k,t) sign(sin 2k t), k 1, 2,...
Выражение sign(x) является функцией знака x :
1, x 0 sign(x)
0, x 0
Функции Радемахера, имеют вид совокупности меандров.
Функции Радемахера
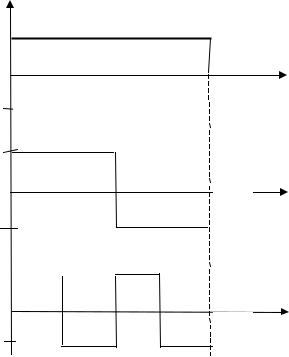
• Три первые функции Радемахера приведены на рисунке:
r(0,t)
r(1,t)
r(2,t)
1 |
|
|
|
|
|
||
-1 0 |
|||
1 |
|
|
|
-1 |
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
-1 0
1
1 |
1 |
2 |
|
1 |
1 |
2 |
|
t
t
t
Функции Радемахера
•Функции Радемахера ортонормированны на интервале 0, 1 , но не образуют полной системы функций, т.к. являются нечетными функциями относительно середины интервала.
В частности, можно подобрать функцию
sign(cos2k t), которая будет ортогональна всем функциям Радемахера. Поэтому, дополнив систему Радемахера функциями, образованными посредством всевозможных произведений функций Радемахера, построим полную систему функций Уолша с различными способами упорядочения.
Диадно-упорядоченная система функций Уолша
• Функции Пэли |
|
pal(k,t) с номером k ( k 0, 1, 2, ...) |
||
|
|
|
|
|
формируются из произведений таких функций Радемахера, |
||||
номера которых определяются по номерам позиций |
||||
двоичного представления числа |
, содержащихk |
единицу. |
||
• |
Если номер функции |
k имеет следующее двоичное |
|
||
|
n разрядное представление: |
|
n 1
k kp 2p ; kp 0,1 ,
то функции системыpПэли0 в общем виде представляются так:
n 1
pal(k,t) r( p 1,t)k p
p 0
Диадно-упорядоченная система функций Уолша
Пример. Построить систем у функций Пэли для случая
N 8, t 0,1 :
pal(0,t) r(0,t); pal(1,t) pal(001,t) r(1,t); pal(2,t) pal(010,t) r(2,t);
pal(3,t) pal(011,t) r(1,t)r(2,t);
pal(4,t) pal(100,t) r(3,t);
pal(5,t) pal(101,t) r(1,t)r(3,t);
pal(6,t) pal(110,t) r(2,t)r(3,t);
pal(7,t) pal(111,t) r(1,t)r(2,t)r(3,t).
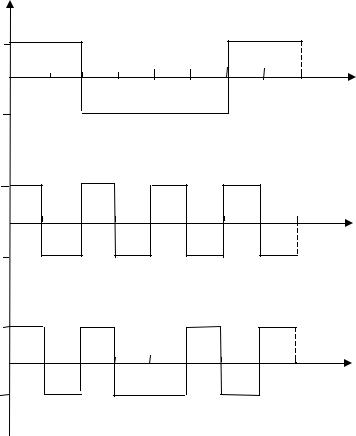
Диадно-упорядоченная система функций Уолша
pal(3,t)
pal(4,t)
pal(5,t)
1
-1 0
1
-1 0
1
-1 0
t
1
t
1
t
1
Система упорядочения по Хармуту
• Систему упорядочения по Хармуту называют системой, функции которой упорядочены по частоте следования или по числу переходов через нулевой уровень (числу смены знаков) на интервале 0,1 . Запишем функции системы
Хармута в форме:
n 1
wal(k,t) sign(cos kp 2p t)
p0
•Анализ показывает, что система Хармута представляет собой систему, в которой чередуются четные и нечетные функции относительно середины временного интервала.
•Свойство четной и нечетной симметрии уподобляет систему Хармута тригонометрической системе функций .
Свойства функций Уолша
1.Ортогональность функций на интервале 0, 1 :
1 |
1, |
k l |
|
|
|
|
. |
wal(k,t)wal(l,t) |
k l |
||
0 |
0, |
|
|
2.Модуль функций Уолша равен 1, т.к. функции принимают только значения :
wal(k,t) 1
3. Среднее значение функций Уолша для всех нулю в силу ортогональности с функцией
1 wal(k,t)dt 0; k 0.
0
k 0 равно
wal(0,t):
4. Функции Уолша являются ортонормированными:1 wal(k,t) 2 dt 1 при любом k .
0