
Яковлева А. 11.03
.pdf
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Яковлева А.
Логин: 05ps36358
Начало тестирования: 2012-03-11 10:48:16 Завершение тестирования: 2012-03-11 11:34:47 Продолжительность тестирования: 46 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 11
Процент правильно выполненных заданий: 34 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица рисков в игре с природой имеет вид:
Тогда средний риск игрока по критерию Байеса относительно рисков будет равен …
2,4
5
2
4,6

 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
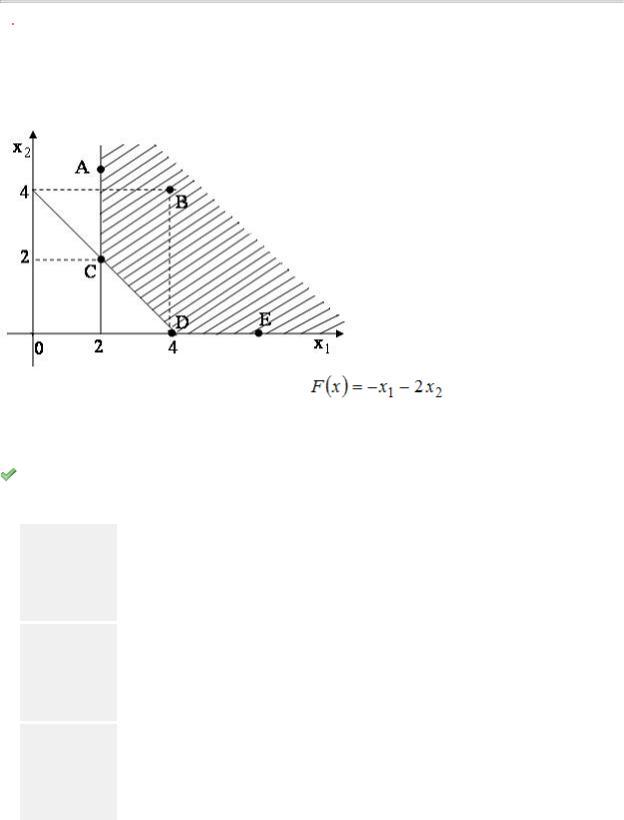
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
Тогда максимальное значение функции |
достигается в точке … |
||
|
|
D |
|
|
|
|
|
|
|
|
|
C
B
точки максимума не существует
Решение:
Построим линию уровня 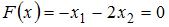 и градиент целевой функции
и градиент целевой функции
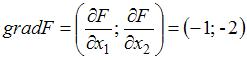 . Тогда целевая функция будет принимать
. Тогда целевая функция будет принимать
наибольшее значение в точке «выхода» линии уровня из области допустимых решений в направлении градиента.
Из рисунка видно, что точкой максимума будет точка D как точка «выхода»
линии уровня 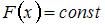 из области допустимых решений в направлении градиента.
из области допустимых решений в направлении градиента.

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Транспортная задача
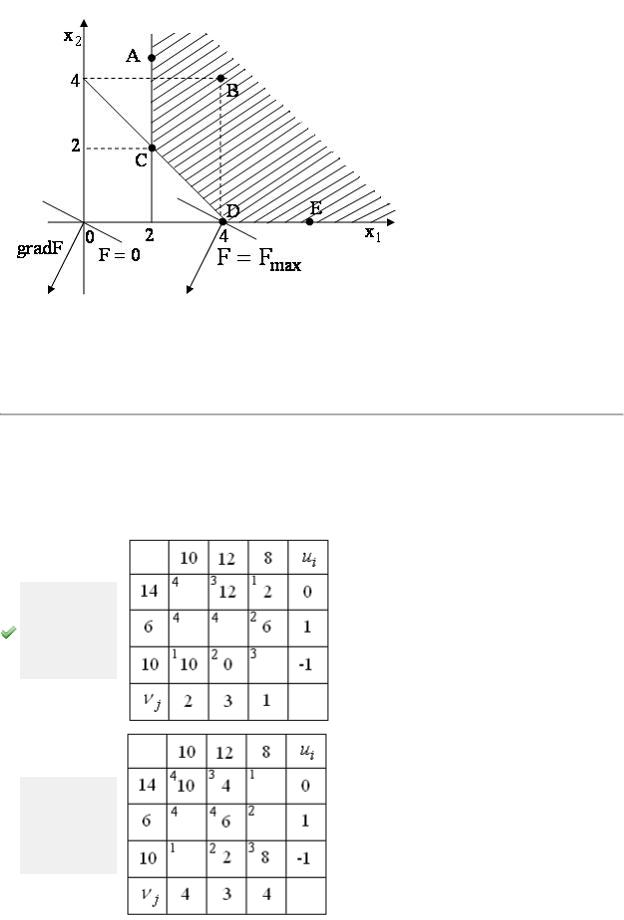
В транспортной задаче оптимальное распределение поставок, найденное по методу потенциалов, имеет вид …
Решение:
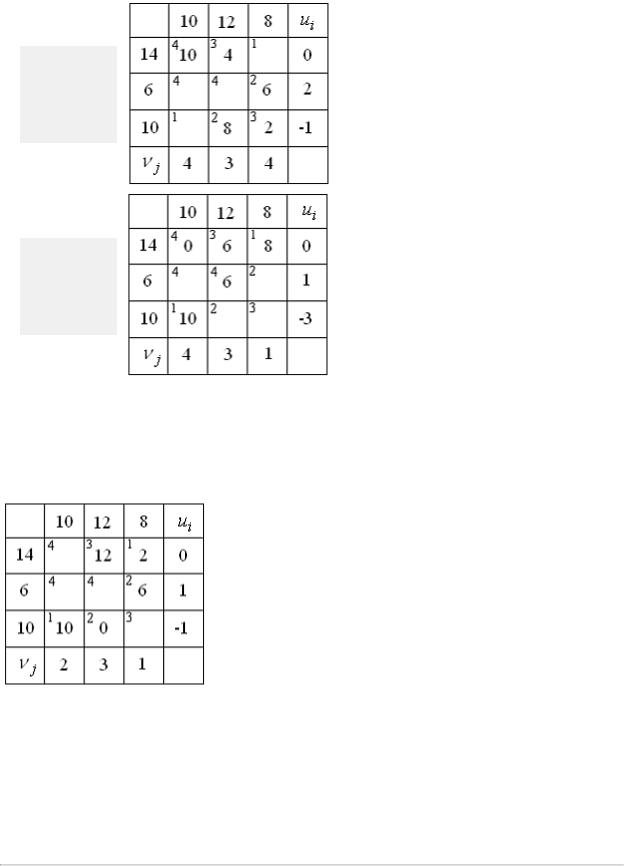
В оптимальном распределении сумма потенциалов для свободных клеток
должна быть меньше или равна тарифу: 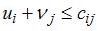 . Этим условиям соответствует распределение, имеющее вид:
. Этим условиям соответствует распределение, имеющее вид:
Действительно,
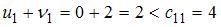 ,
,
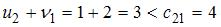 ,
,
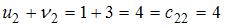 ,
,
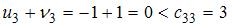 .
.

 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,

критический путь имеет вид 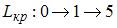 . Тогда значение параметра
. Тогда значение параметра 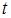 не может быть равно …
не может быть равно …
19
12
13
16

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции 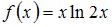 имеет вид …
имеет вид …

Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле
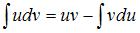 . Тогда
. Тогда
.

 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка 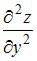 функции
функции 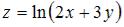 имеет вид
имеет вид
…

Решение:
При вычислении частной производной функции 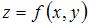 по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Свойства определенного интеграла
Среднее значение функции 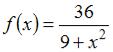 на отрезке
на отрезке 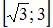 равно …
равно …

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Минимум функции 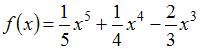 равен …
равен …
0

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Предел функции
Предел 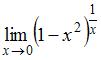 равен …
равен …
1
0

Решение:
Данный предел можно вычислить с использованием второго замечательного
предела и его следствий вида 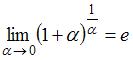 . Тогда:
. Тогда:
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Асимптоты графика функции
Наклонная асимптота графика функции 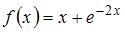 задается уравнением вида …
задается уравнением вида …
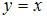 , при
, при 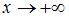
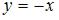 , при
, при 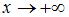
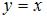 , при
, при 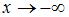

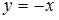 , при
, при 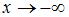

 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Производные первого порядка
Производная функции 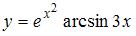 равна …
равна …
Решение:

 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Область определения функции
Область определения функции 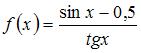 имеет вид …
имеет вид …
