
Скогорева А. 11.03
.pdf
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Скогорева А.
Логин: 05ps36356
Начало тестирования: 2012-03-11 10:47:11 Завершение тестирования: 2012-03-11 11:32:52 Продолжительность тестирования: 45 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 19
Процент правильно выполненных заданий: 59 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Линейные операции над матрицами
Дана матрица 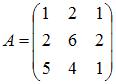 . Тогда матрица
. Тогда матрица 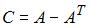 равна …
равна …

 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Вычисление определителей

Определитель  равен …
равен …
91
97
83
89

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Ранг матрицы
Дана матрица 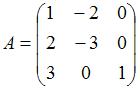 . Тогда ранг матрицы
. Тогда ранг матрицы 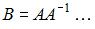
равен 3
равен 1

равен 0
не определен
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю.
1) Проверим существование обратной матрицы 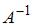 , для чего вычислим определитель матрицы
, для чего вычислим определитель матрицы  (разложением по третьему столбцу)
(разложением по третьему столбцу)
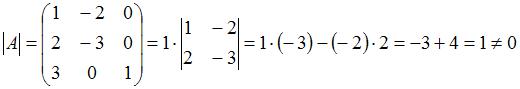 ,
,
следовательно обратная матрица существует.
2) Тогда матрица 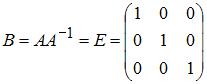 , то есть единичной матрице размерности 3×3. Следовательно, существует ненулевой минор третьего
, то есть единичной матрице размерности 3×3. Следовательно, существует ненулевой минор третьего
порядка: 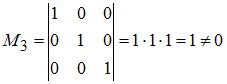 , то есть ранг матрицы равен трем.
, то есть ранг матрицы равен трем.

 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Определение линейного пространства
Линейное пространство 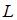 не обладает свойством …
не обладает свойством …
для любого 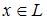 может существовать несколько противоположных элементов
может существовать несколько противоположных элементов 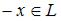

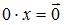 для любого
для любого 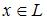
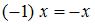 для любого
для любого 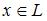
нейтральный элемент 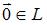 является единственным
является единственным
Решение:
Линейное пространство обладает свойствами:
1. Нейтральный элемент 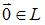 является единственным.
является единственным.
2. 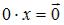 для любого
для любого 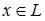 .
.
3. Для любого 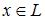 противоположный элемент
противоположный элемент 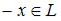 является единственным. 4.
является единственным. 4. 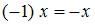 для любого
для любого 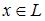 .
.
5. 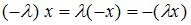 для любых
для любых 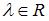 и
и 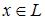 .
.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Системы линейных уравнений
Метод Гаусса для решения систем линейных уравнений заключается …
в последовательном исключении переменных
впоследовательном исключении свободных членов
внахождении обратной матрицы

в вычислении вспомогательных определителей системы
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Обратная матрица
Для матрицы 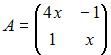 не существует обратной, если
не существует обратной, если 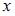 равно …
равно …
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABC задачи линейного программирования имеет вид:
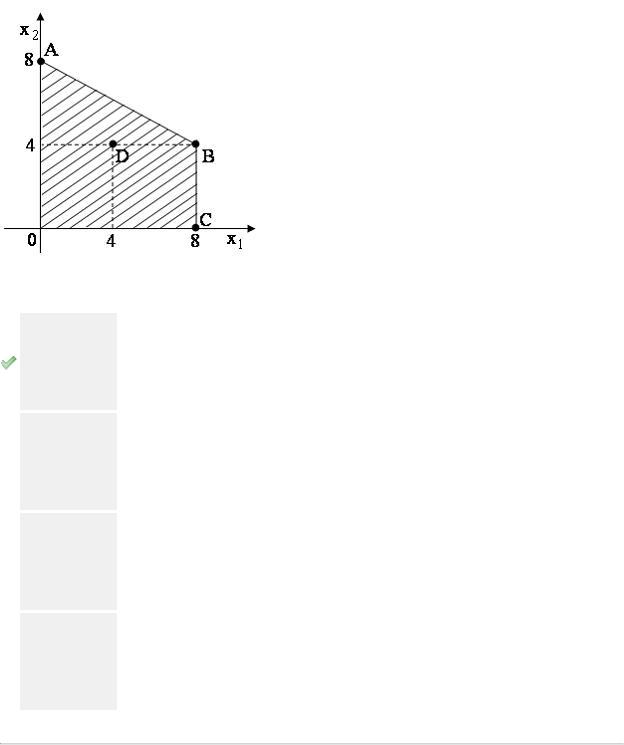
Тогда максимальное значение функции  достигается в точке …
достигается в точке …
B
D
A
C
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Транспортная задача

Транспортная задача
будет закрытой, если …
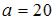 ,
, 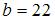
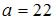 ,
, 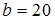
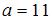 ,
, 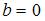
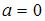 ,
, 

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Сетевое планирование и управление
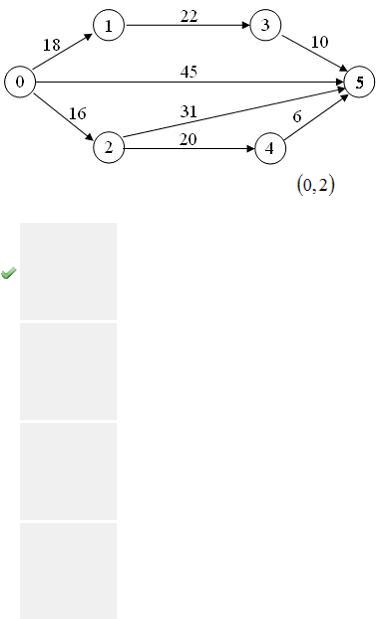
Сетевой график изображен на рисунке
Тогда полный резерв времени работы |
равен … |
3
8
0
11
Решение:
Выделим полные пути: 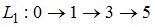 ,
, 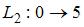 ,
, 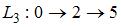 ,
, 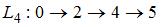 ,
,
вычислим их длины: 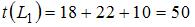 ,
, 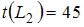 ,
, 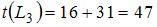 ,
,
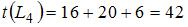 . Тогда критическим будет путь
. Тогда критическим будет путь 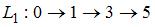 с наибольшей длиной
с наибольшей длиной 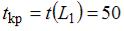 . Полный резерв времени работы
. Полный резерв времени работы 
равен разности между 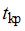 и наибольшей длиной (
и наибольшей длиной (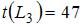 ) пути, проходящей через эту работу. Следовательно,
) пути, проходящей через эту работу. Следовательно, 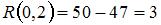 .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Теория игр: игры с природой
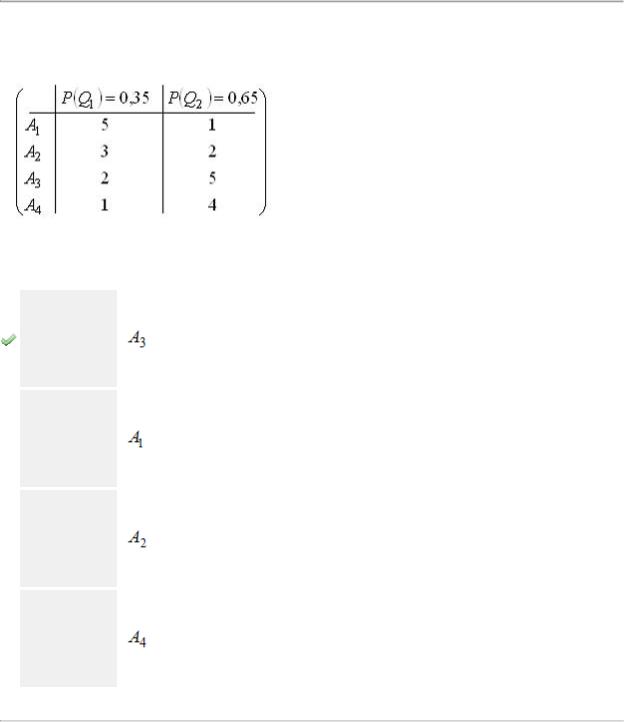
Матрица выигрышей в игре с природой имеет вид:
Тогда оптимальной по критерию Байеса относительно выигрышей будет стратегия …
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 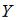 на
на  имеет вид
имеет вид
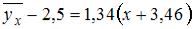 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 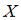 равно …
равно …
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Проверка статистических гипотез
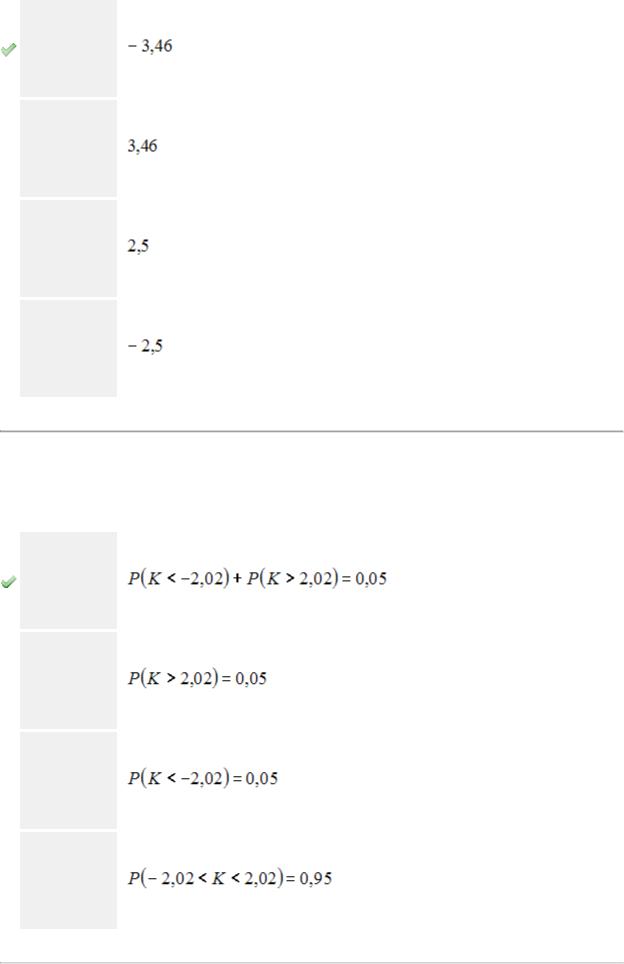
Двусторонняя критическая область может определяться из соотношения …
