Мантлер И. 11
.pdf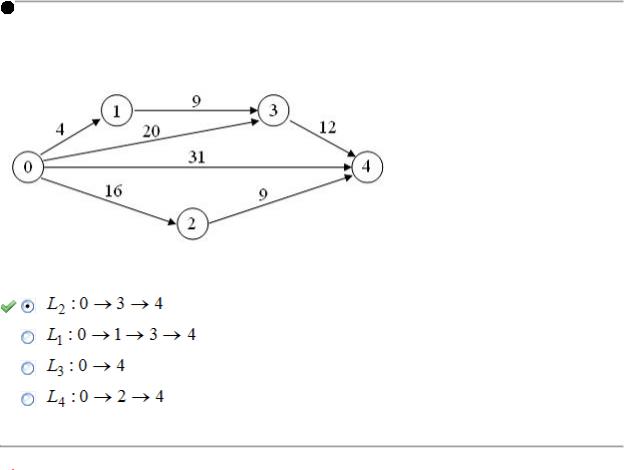
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Мантлер И.
Логин: 05ps36352
Начало тестирования: 2012-03-11 10:49:28 Завершение тестирования: 2012-03-11 11:42:06 Продолжительность тестирования: 52 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 9
Процент правильно выполненных заданий: 28 %
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
критический путь имеет вид …
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Транспортная задача
В транспортной задаче распределение поставок задано таблицей:
Тогда значение потенциала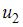 
будет равно …
3
0
4
2
Решение:
Сумма потенциалов для занятых клеток должна быть равна тарифу. Следовательно,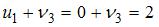 
, то есть 
. 
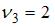, то есть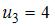 
.
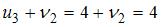, то есть 
. 
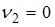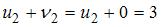, то есть 
.
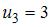ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица рисков в игре с природой имеет вид:
Тогда оптимальной по критерию Байеса относительно рисков будет стратегия
…
Решение:
Вычислим средние риски игрока: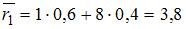 
, 
, 
,
.
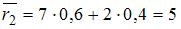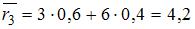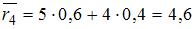Так как наименьший средний риск равен 3,8, то оптимальной будет стратегия
.
ЗАДАНИЕ N 4 сообщить об ошибке
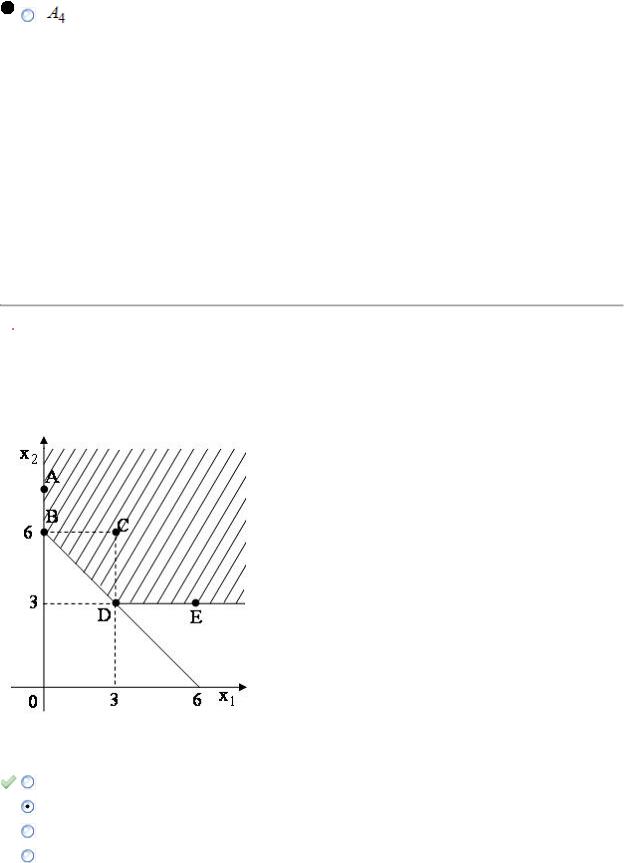
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
Тогда минимальное значение функции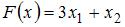 
равно …
6
0
18
12
Решение:
Построим линию уровня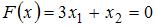 
и градиент целевой функции
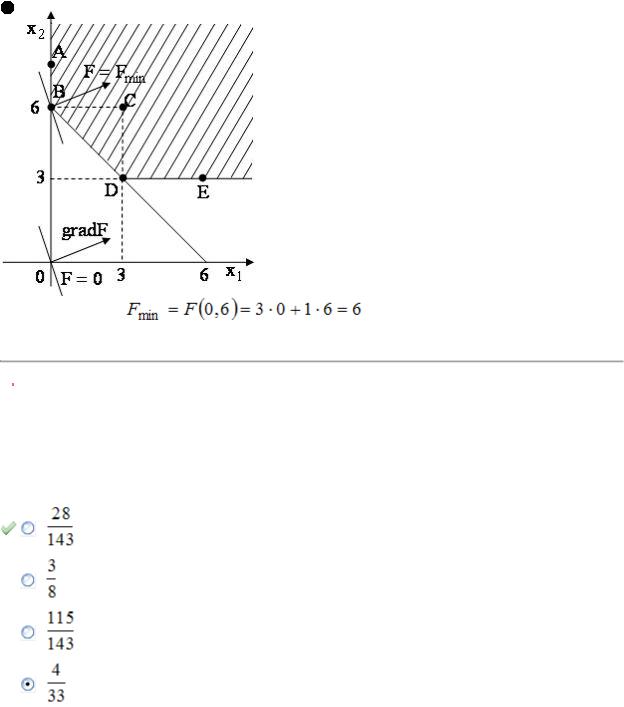
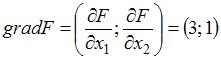. Тогда целевая функция будет принимать наименьшее значение в точке «входа» линии уровня в область допустимых
решений в направлении градиента. Это точка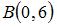 
.
Следовательно, |
. |
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В урну, в которой лежат 6 белых и 5 черных шаров добавляют два белых шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
Решение:
Введем обозначения событий: 
–
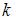-ый вынутый шар будет белым, A – все три шара будут белыми. Тогда 
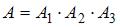, и так как по условию задачи
события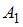 
, 
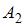и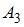 
зависимы, то
.
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
0
Решение:
Для вычисления события A (сумма выпавших очков будет не меньше девяти)
воспользуемся формулой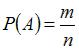 
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны
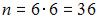элементарных исходов испытания, из которых благоприятствующими являются исходы вида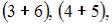 
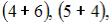
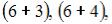
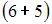и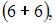 
то есть 
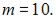Следовательно,
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина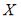 
задана плотностью распределения вероятностей:
Тогда ее дисперсия равна …
Решение:
Дисперсию непрерывной случайной величины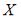 
можно вычислить по формуле
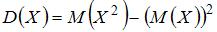. Тогда
.
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина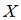 
задана законом распределения вероятностей:
Тогда значения a и b могут быть равны …
Решение:
Так как сумма вероятностей возможных значений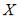 
равна 1, то 
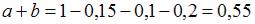. Этому условию удовлетворяет ответ:
.
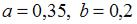ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Точечные оценки параметров распределения
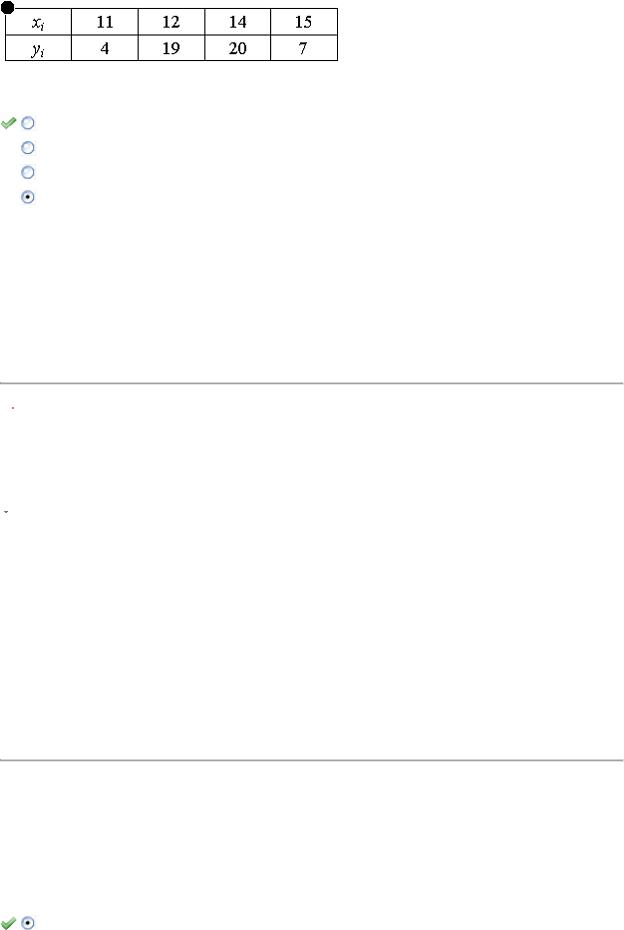
Из генеральной совокупности извлечена выборка объема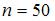 
:
Тогда несмещенная оценка математического ожидания равна …
13,14
13,0
13,34
13,2
Решение:
Несмещенная оценка математического ожидания вычисляется по формуле
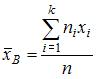. То есть 
.
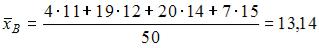ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида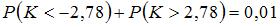 
можно определить …
двустороннюю критическую область 
правостороннюю критическую область
левостороннюю критическую область 
область принятия гипотезы
Решение:
Данное соотношение определяет двустороннюю критическую область, так как двусторонней называют критическую область, определяемую, например,
соотношением вида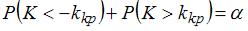 
, где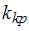 
– положительное число, а 
– уровень значимости.
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал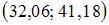 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
36,62
36,52
9,12
73,24
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии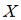 
на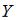 
имеет вид
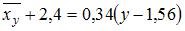. Тогда выборочное среднее признака 
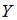равно …
Решение:
Выборочное уравнение прямой линии регрессии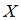 
на 
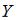имеет вид
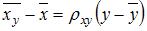. Тогда выборочное среднее признака 
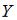равно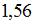 
.
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема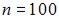 
, полигон относительных частот которой имеет вид:
Тогда число вариант |
в выборке равно … |
||
|
|
37 |
|
|
|
||
63
100
36
Решение:
Вычислим предварительно относительную частоту варианты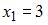 
как 
. Тогда из определения относительной
частоты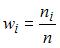 
, получаем, что 
.
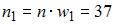ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Характеристики вариационного ряда
Размах варьирования вариационного ряда 3, 4, 4, 4, 5, 7, 8, 10, 11, 12, 14, 14 равен …
11
4
9
17
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Функции полезности
В теории потребления предполагается, что функция полезности потребителя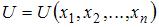 
обладает свойством …
Решение:
Функция полезности потребителя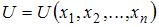 
не обладает свойством
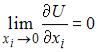, так как в теории потребления предполагается, что небольшой прирост блага при его первоначальном отсутствии резко увеличивает
полезность, то есть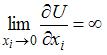 
.
Функция полезности не обладает свойством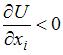 
, так как с ростом объема потребления блага полезность растет, то есть 
.
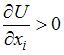Функция полезности не обладает свойством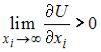 
, так как при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению
полезности, то есть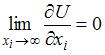 
.
А так как с ростом объема потребления блага скорость роста полезности
замедляется, то функция полезности обладает свойством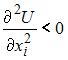 
.
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Сетевое планирование и управление
Матрица коэффициентов полных затрат статической линейной модели Леонтьева может иметь вид …