3

представлены вектором 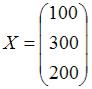. Тогда объемы конечного продукта будут представлены вектором …

Решение:

Статическая линейная модель Леонтьева в матричной форме моделируется системой , где – единичная матрица. Следовательно, объемы конечного продукта определяются как , то есть

ЗАДАНИЕ N 31 сообщить об ошибке

Тема: Функции спроса и предложения

Даны функции спроса 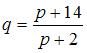и предложения , где p – цена товара. Если равновесный объем спроса-предложения равен , то значение параметра равно …

Решение:

Из условия , или , определим равновесную цену спросапредложения:. Подставив значения и в уравнение

, получим искомое значение .

ЗАДАНИЕ N 32 сообщить об ошибке

Тема: Функции полезности

Функция полезности потребителя имеет вид , а оптимальное потребление: , . Тогда предельная полезность блага равна …

0,8

6,25

0,16

1,25

Определитель равен …

91

97

83

89

ЗАДАНИЕ N 3 сообщить об ошибке

Тема: Ранг матрицы

Дана матрица . Тогда ранг матрицы

равен 3

равен 1

равен 0

не определен

Решение:

Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю.

1) Проверим существование обратной матрицы , для чего вычислим определитель матрицы (разложением по третьему столбцу)

,

следовательно обратная матрица существует.

2) Тогда матрица , то есть единичной матрице размерности 3×3. Следовательно, существует ненулевой минор третьего

порядка: , то есть ранг матрицы равен трем.

ЗАДАНИЕ N 4 сообщить об ошибке

Тема: Определение линейного пространства

Линейное пространство не обладает свойством …

для любого может существовать несколько противоположных элементов

для любого

для любого

нейтральный элемент является единственным

Решение:

Линейное пространство обладает свойствами:

1. Нейтральный элемент является единственным.

2. для любого .

3. Для любого противоположный элемент является единственным. 4. 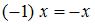для любого .

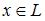5. для любых и .

ЗАДАНИЕ N 5 сообщить об ошибке

Тема: Системы линейных уравнений

Метод Гаусса для решения систем линейных уравнений заключается …

в последовательном исключении переменных

впоследовательном исключении свободных членов

внахождении обратной матрицы

в вычислении вспомогательных определителей системы

ЗАДАНИЕ N 6 сообщить об ошибке

Тема: Обратная матрица

Для матрицы не существует обратной, если равно …

ЗАДАНИЕ N 7 сообщить об ошибке

Тема: Линейное программирование: графическое задание области допустимых решений

Область допустимых решений OABC задачи линейного программирования имеет вид:

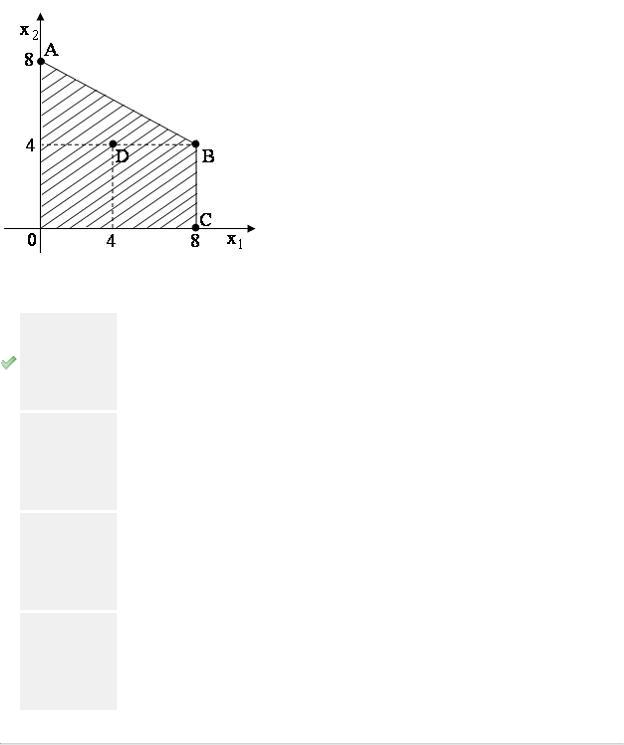
Тогда максимальное значение функции достигается в точке …

B

D

A

C

ЗАДАНИЕ N 8 сообщить об ошибке

Тема: Транспортная задача

Транспортная задача

будет закрытой, если …

,

,

,

,

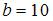
ЗАДАНИЕ N 9 сообщить об ошибке

Тема: Сетевое планирование и управление

Сетевой график изображен на рисунке

3

8

0

11

Решение:

Выделим полные пути: , , , ,

вычислим их длины: , , ,

. Тогда критическим будет путь с наибольшей длиной . Полный резерв времени работы