
3
.pdf
 ,
, 
 ,
, 
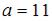 ,
, 
 ,
, 

 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица рисков в игре с природой имеет вид:
Тогда средний риск игрока по критерию Байеса относительно рисков будет равен …
2,4
5
2
4,6
Решение:
Определим предварительно неизвестную вероятность  и вычислим средние риски игрока:
и вычислим средние риски игрока:
 ,
,
 ,
,
 ,
,
 .
.
Тогда наименьший средний риск игрока будет равен 2,4.

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Сетевое планирование и управление

Сетевой график изображен на рисунке
Тогда, для изменения критического пути, продолжительность работы  можно увеличить на …
можно увеличить на …

 7 дней
7 дней  5 дней
5 дней
 3 дня
3 дня  1 день
1 день
Решение:
Выделим полные пути:  ,
,  ,
,  ,
,  ,
,
вычислим их длины: 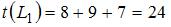 ,
, 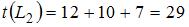 ,
,  ,
,  . Тогда критическим будет путь
. Тогда критическим будет путь  с наибольшей длиной
с наибольшей длиной  .
.
Чтобы критический путь изменился надо продолжительность работы  увеличить, например, на 7 дней, так как
увеличить, например, на 7 дней, так как  .
.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии  на
на  имеет вид
имеет вид
 . Тогда выборочный коэффициент корреляции может быть равен …
. Тогда выборочный коэффициент корреляции может быть равен …


 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид  . Тогда конкурирующей может являться гипотеза …
. Тогда конкурирующей может являться гипотеза …
Решение:
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию 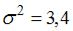 противоречит
противоречит  .
.

 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Проведено четыре измерения (без систематических ошибок) некоторой
случайной величины (в мм): 8, 9,  , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …
, 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …
2,5
2,0
0
1,5
Решение:
Вычислим предварительно значение  . Так как несмещенная оценка
. Так как несмещенная оценка
математического ожидания вычисляется по формуле:  , то
, то
 . Следовательно,
. Следовательно, 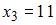 .
.

Для вычисления выборочной дисперсии применим формулу 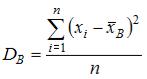 .
.
Тогда  .
.

 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема  , полигон относительных частот которой имеет вид:
, полигон относительных частот которой имеет вид:
Тогда число вариант |
в выборке равно … |
37
63
100
36
Решение:
Вычислим предварительно относительную частоту варианты  как
как  . Тогда из определения относительной
. Тогда из определения относительной
частоты  , получаем, что
, получаем, что  .
.

 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Интервальные оценки параметров распределения

Дан доверительный интервал  для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
…
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде
симметричного интервала 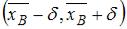 , где точечная оценка
, где точечная оценка
математического ожидания  , а точность оценки
, а точность оценки  . В случае
. В случае
уменьшения объема выборки точность оценки ухудшается, то есть значение  будет больше 2,13.
будет больше 2,13.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Характеристики вариационного ряда
Медиана вариационного ряда 2, 3, 5, 6, 7, 9,  , 12, 13, 15, 16, 18 равна 10. Тогда значение варианты
, 12, 13, 15, 16, 18 равна 10. Тогда значение варианты  равно …
равно …
11
10
12
9

 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Системы линейных уравнений
Система  будет …
будет …

 совместной и неопределенной
совместной и неопределенной  несовместной и неопределенной
несовместной и неопределенной
 совместной и определенной
совместной и определенной  несовместной и определенной
несовместной и определенной

Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем
расширенную матрицу системы и преобразуем ее: 

 . Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
. Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.

 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Вычисление определителей
Корень уравнения  равен …
равен …
– 3 0 3
– 9
Решение:
Определитель третьего порядка можно вычислить, например, разложением по элементам первой строки:
 . По условию задачи определитель должен равняться
. По условию задачи определитель должен равняться  , то есть
, то есть  . Следовательно,
. Следовательно,
 .
.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Определение линейного пространства
Среди представленных множеств линейное пространство образует …

 множество всех комплексных чисел
множество всех комплексных чисел

 множество всех натуральных чисел
множество всех натуральных чисел  множество всех положительных иррациональных чисел
множество всех положительных иррациональных чисел
 множество всех отрицательных рациональных чисел
множество всех отрицательных рациональных чисел
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен единице, если
равен единице, если  принимают значения
принимают значения
…

 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы  и
и  . Если
. Если  , то след матрицы
, то след матрицы  равен …
равен …
11
85
12
41
Решение:
Матрица  находится следующим образом:
находится следующим образом:
 .
.
След матрицы равен сумме элементов главной диагонали:  .
.

 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Обратная матрица
Для матрицы  обратная матрица равна …
обратная матрица равна …

 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина  задана функцией распределения вероятностей
задана функцией распределения вероятностей
Тогда вероятность |
равна … |
0,54
0,38
0,70
0,86

Решение:
Так как по определению  , то случайную величину
, то случайную величину  можно задать законом распределения вероятностей вида
можно задать законом распределения вероятностей вида
Следовательно, |
. |

 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Вероятность поражения цели первым стрелком равна 0,9, а вторым – 0,85. Оба стрелка стреляют одновременно. Тогда вероятность поражения цели, равна …
0,985
0,775
0,875
1,75
Решение:
Введем обозначения событий: 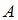 (цель поражена первым стрелком),
(цель поражена первым стрелком),  (цель поражена вторым стрелком). Так как эти события независимы, то искомую вероятность можно вычислить как:
(цель поражена вторым стрелком). Так как эти события независимы, то искомую вероятность можно вычислить как:

 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина  задана плотностью распределения
задана плотностью распределения
вероятностей  . Тогда математическое ожидание a и среднее квадратическое отклонение
. Тогда математическое ожидание a и среднее квадратическое отклонение  этой случайной величины равны …
этой случайной величины равны …

Решение:
Плотность распределения вероятностей нормально распределенной случайной
величины  имеет вид
имеет вид  , где
, где  ,
,  . Поэтому
. Поэтому  .
.

 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Определение вероятности
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
Решение:
Для вычисления вероятности искомого события воспользуемся формулой
 , где
, где  – площадь меньшего круга, а
– площадь меньшего круга, а 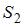 – площадь большего круга.
– площадь большего круга.
Следовательно,  .
.
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Предел функции
Предел  равен …
равен …
