
- •Кафедра автоматизации и информационных систем
- •2011 Постановки задач по лабораторным работам Задача 1. Математическое моделирование и настройка сар по отклонению с использованием поисковых методов оптимизации
- •Задача 2. Натурно-математическое моделирование и настройка сар по отклонению с использованием поисковых методов оптимизации
- •Задача 3. Математическое моделирование и настройка сар по контролируемым возмущениям с использованием поисковых методов оптимизации.
- •Задача 4. Численные исследования идентификаторов на базе замкнутых динамических систем.
- •А) возврат чистого кредита; б) начисление на возвращенный кредит; в) возврат кредита с процентами.
- •А) модель предприятия в текущий момент времени; б) интегральная модель предприятия.
- •Задача 2. Исследование и оптимизация муниципальной финансово-промышленной группы на базе математического имитационного моделирования и поисковых методов в условиях неопределенности.
Задача 2. Исследование и оптимизация муниципальной финансово-промышленной группы на базе математического имитационного моделирования и поисковых методов в условиях неопределенности.
Постановка задачи.
Дано. 1. Общая структура упрощенной модели МФПГ, соответствующая рисунку 1.
2.
Модель предприятия, производящего
продукцию
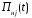 в текущий момент времени, представленная
также как и в предыдущем случае в виде
суммы двух составляющих
в текущий момент времени, представленная
также как и в предыдущем случае в виде
суммы двух составляющих


 ,
(26)
,
(26)
где
 – выпуск продукции предприятием
– выпуск продукции предприятием ;
;
 –возврат
взятого предприятием
–возврат
взятого предприятием
 кредита с процентами;
кредита с процентами;
индекс «н» здесь и далее означает результаты моделирования с учетом неопределенности.
2.1.
При построении модели выпуска продукции
в текущий момент времени введены
дополнительные по сравнению с предыдущим
примером соображения, заключающиеся в
том, что на детерминированную составляющую
выпуска продукции аддитивно налагается
случайная составляющая, описываемая
стационарным гауссовским законом
распределения вероятностей

 ,
(27)
,
(27)
где
 и
и -
математическое ожидание и среднее
квадратическое отклонение случайной
составляющей
-
математическое ожидание и среднее
квадратическое отклонение случайной
составляющей ,
либо нестационарным законом распределения
(55) с изменяющимися математическим
ожиданием и средним квадратическим
отклонением, в частности, с их ограниченным
возрастанием с течением времени
,
либо нестационарным законом распределения
(55) с изменяющимися математическим
ожиданием и средним квадратическим
отклонением, в частности, с их ограниченным
возрастанием с течением времени
 (28)
(28)
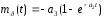 ,
(29)
,
(29)
где
 - постоянные коэффициенты.
- постоянные коэффициенты.
Графически
модели случайной составляющей
 представлены на рисунках 19 и 20.
представлены на рисунках 19 и 20.
Рисунок
9 - Плотность нормального распределения
составляющей

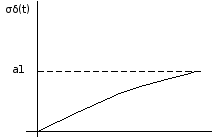
t
Рисунок 10 - Зависимость σδ от времени
Окончательно
модель выпуска продукции предприятия
 в текущий момент времени примет вид
в текущий момент времени примет вид
 .
(30)
.
(30)
Графически модель (30) с учетом выражений (27)-(29) представлена на рисунке 11.

а)

б)
а)
импульс инвестиций; б) реакция объекта
на инвестиции в виде импульса: 1 –
детерминированная составляющая
 модели;
2 -mδ(t);
3,4 – граничные траектории возможного
изменения Пр(t).
модели;
2 -mδ(t);
3,4 – граничные траектории возможного
изменения Пр(t).
Рисунок 11 - Графическое представление модели выпуска продукции
Интегральная
модель, характеризующая накопление
(интегрирование) выпуска продукции за
интервал времени от
 до
до ,
представлена в виде
,
представлена в виде
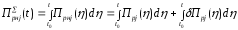 ,
(31)
,
(31)
где
 соответствует выражению (2).
соответствует выражению (2).
2.2. При построении модели возврата кредита введены следующие дополнительные по сравнению с предыдущим примером соображения:
-
возврат кредита в каждый момент времени
не превышает установленной величины,
равной
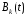 (формула 6), но может быть меньше в
зависимости от неопределенности модели
выпуска продукции;
(формула 6), но может быть меньше в
зависимости от неопределенности модели
выпуска продукции;
-
дополнительные санкции в данном примере
за негативные для банка отклонения от
зафиксированной траектории возврата
кредита
 не устанавливаются;
не устанавливаются;
-
процент возврата кредита
 определяется
выражением (7).
определяется
выражением (7).
При
таких условиях неопределенность
 ,
аддитивно связанную с детерминированной
составляющей модели возврата кредита
(6), целесообразно описать односторонним
несимметричным законом распределения
вероятностей, в частности, экспоненциальным
законом, аналитическое выражение функции
плотности вероятностей которого имеет
вид
,
аддитивно связанную с детерминированной
составляющей модели возврата кредита
(6), целесообразно описать односторонним
несимметричным законом распределения
вероятностей, в частности, экспоненциальным
законом, аналитическое выражение функции
плотности вероятностей которого имеет
вид
 ,
(32)
,
(32)
где
 - параметр экспоненциального распределения.
- параметр экспоненциального распределения.
Для
экспоненциального распределения
математическое ожидание
 величины
величины и ее среднее квадратическое отклонение
и ее среднее квадратическое отклонение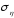 одинаковы и равны
одинаковы и равны .
.
Графический
вид плотности экспоненциального
распределения с параметром
 приведен на рисунке 12.
приведен на рисунке 12.

Рисунок 12 - Плотность экспоненциального распределения
Неопределенность
 обусловлена,
главным образом, наличием составляющей
обусловлена,
главным образом, наличием составляющей ,
характеристики закона распределения
которой
,
характеристики закона распределения
которой и
и приняты нестационарными. Поэтому
математическое ожидание
приняты нестационарными. Поэтому
математическое ожидание и среднее квадратическое отклонение
и среднее квадратическое отклонение закона распределения (60) также взяты
зависящими от времени с помощью функции
вида
закона распределения (60) также взяты
зависящими от времени с помощью функции
вида
 ,
(33)
,
(33)
где a4 – постоянный коэффициент.
При этих соображениях, включая и соображения, сформулированные для модели возврата кредита предыдущего примера, эта модель имеет вид
 (34)
(34)
Составляющая
 описывается следующими уравнениями
описывается следующими уравнениями
 (35)
(35)
 ;
(36)
;
(36)
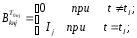 (37)
(37)
 ;
;
 .(38)
.(38)
Составляющая
 выражения (64) рассчитывается по формуле
(6) и представляет собой постоянную
величину, определённую на интервале
времени Т0от момента
выражения (64) рассчитывается по формуле
(6) и представляет собой постоянную
величину, определённую на интервале
времени Т0от момента до момента
до момента .
Соответствующая ей величина
.
Соответствующая ей величина выражения (36) также будет постоянной.
Однако за счёт введения неопределённости
δВ с односторонним законом распределения
(60) она будет меньше, чем
выражения (36) также будет постоянной.
Однако за счёт введения неопределённости
δВ с односторонним законом распределения
(60) она будет меньше, чем на величину А. Примем А равной максимальному
значению математического ожидания
случайной величины δВ, т.е.
на величину А. Примем А равной максимальному
значению математического ожидания
случайной величины δВ, т.е.
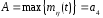 .
(39)
.
(39)
При этом уменьшение величины текущего
возврата кредита приведёт, соответственно,
к увеличению времени
 полного
возврата кредита
полного
возврата кредита за счёт увеличения интервала
за счёт увеличения интервала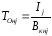 .
Составляющая
.
Составляющая (t)
выражения (34) определяется, как уже было
отмечено, формулой (7).
(t)
выражения (34) определяется, как уже было
отмечено, формулой (7).
Графически модель возврата кредита в условиях неопределённости представлена на рисунке 13. Для наглядности представления модель возврата кредита в условиях неопределённости (кривые приведены сплошными линиями) приведёна на этом рисунке в сопоставлении с детерминированной моделью (штрихпунктирные линии). Кривые на рисунках 13в, 13г для обоих случаев совпадают, а S1=S2,S3=S4 ,S5=S6 (рисунки 13а, 13б и 13в). Как видно из графиков, время полного возврата кредита в условиях неопределённости увеличивается на ΔТ = Тон - То.
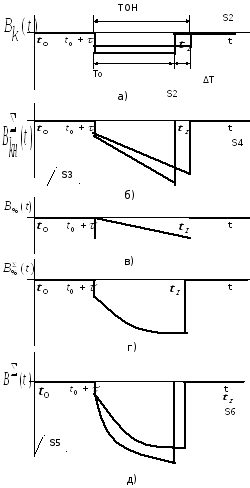
Рисунок 13 - Графическое представление модели возврата в условиях
неопределённости
3. Аналитически модель банка в интегральной форме записывается в виде, аналогичном (15)
 (40)
(40)
где
 представлено соотношениями (34)-(38), с той
лишь разницей, что все члены выражения
(34) – положительные.
представлено соотношениями (34)-(38), с той
лишь разницей, что все члены выражения
(34) – положительные.
Графически выражение (40) имеет вид, представленный на рисунке 14. Здесь модель банка (40) (сплошная линия), также как и модель возврата кредита (рисунок 13), дана в сопоставлении с моделью (15) (штрихпунктирная линия).

Рисунок 14 - Графическое представление модели банка в условиях
неопределённости
4. Модель МФПГ в интегральном виде выражается при помощи траектории прибыли
 (41)
(41)
где
составляющая
 характеризует суммарную прибыль
предприятий ПП1 и ПП2
характеризует суммарную прибыль
предприятий ПП1 и ПП2
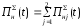 ,
(42)
,
(42)
где
 определяется по формулам (26), (30), (34)-(38),
а ПБн(t)
– выражением (40).
определяется по формулам (26), (30), (34)-(38),
а ПБн(t)
– выражением (40).
5. Управляющие воздействия, ограничения и критерии в данном примере совпадают с соответствующими переменными и показателями предыдущего примера, т.е. в качестве управляющих воздействий рассматриваются: 1) заданные траектории изменения инвестиции; 2) процент начисления кредита со стороны банка. Ограничения по инвестиции определяются посредством (20), а критерии соответствуют выражениям (21) – (25).
6. Методы оптимизации, такие как поисковые процедуры, например основанные на методах деформируемых конфигураций.
Требуется. Найти оптимальные размеры инвестиций каждому предприятию по критериям (21) -(25) с учетом ограничений (20).
