3.3 Анализ чувствительности типовой системы управления к изменениям параметров объекта.

В общем случае, объект управления является нестационарным, то есть со временем может изменять свойства и структуру. Поэтому синтез управляющей системы по расчету настроечных параметров алгоритма управления должен быть адаптивным. Необходимость в адаптации обосновывается анализом чувствительности, который заключается в исследовании изменения надежности и качества управления при изменении параметров объекта и неизменяемых настроечных параметрах управляющей системы. Модель объекта управления характеризуется параметрами: которые принимаются на номинальные и используются в расчете управляющей системы:

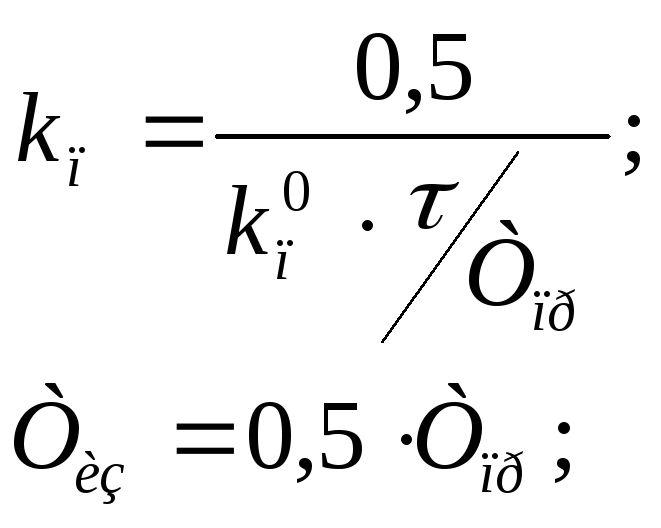
Поэтому при изменении параметров объекта пропорционально должны изменяться настроечные параметры управляющей системы:

Такие настроечные параметры называются адаптивными, позволяют оптимизировать управление при любых изменениях объекта, однако требуют периодической идентификации модели объекта. В случае нечувствительности системы к таким изменениям не имеет смысла реализовывать дополнительные затраты на алгоритмизацию. Рассмотрим актуальность такой адаптации, анализ произведем по изменению надежности.

Методика анализа:

1. Анализ проводится в отдельности для параметров модели объекта . В качествевыбираются граничные условия по условию задачи или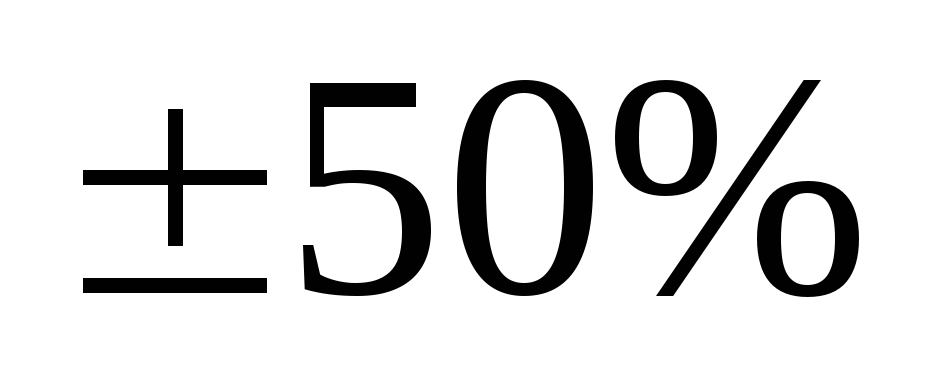от номинального значения параметра:

2. Каждый диапазон изменения разбивается на исследуемые участки не меньше 5 дискретов, то есть разбиваем диапазон .

3. Для каждого выделенного диапазона по исследуемому параметру при условии, если остальные принимаются номинальными, проводится исследование устойчивости системы или определяются показатели качества управления без изменения настроечных параметров управляющей системы.

.

Проводим исследование по каждому параметру:

1. ; для каждого случая строим годограф и определяем запасы устойчивостии:

ω	0	0,01	0,05	0,1	0,5	1	1,05	1,5	2	2,5	3
А(ω)	0,00	10186,70	407,47	101,87	4,08	1,02	0,93	0,46	0,26	0,17	0,12
φ(ω)	0,00	-0,01	-0,06	-0,13	-0,65	-1,30	-1,36	-1,94	-2,58	-3,21	-3,83

Результаты исследования построим на графике (рисунок 21):

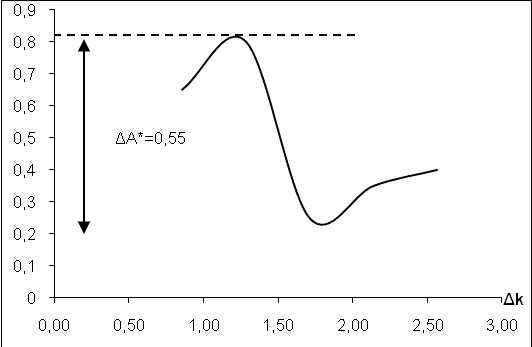
Рисунок 21 - Графики запасов устойчивости ипо

Увеличение коэффициента передачи объекта приводит к изменению запасаи, то есть потере надежности. Таким образом, система управления чувствительна к изменению коэффициента передачипона 50%, а почувствительна на.

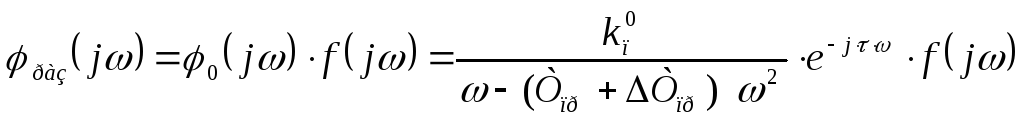2. ; для каждого случая строим годограф и определяем запасы устойчивостии:

ω	0	0,01	0,05	0,1	0,5	1	1,05	1,5	2	2,5	3
А(ω)	0,00	10186,70	407,47	101,87	4,08	1,02	0,93	0,46	0,26	0,17	0,12
φ(ω)	0,00	-0,01	-0,06	-0,13	-0,65	-1,30	-1,36	-1,94	-2,58	-3,21	-3,83

Результаты исследования построим на графике (рисунок 22):

Рисунок 22 - Графики запасов устойчивости ипо

Увеличение коэффициента передачи объекта не приводит к изменению запасаи, то есть потере надежности. Таким образом, система управления не чувствительна к изменению коэффициента передачипои по(* =0;*=0).

Таким образом, система нечувствительна к изменениям настроечных параметров, значит, не имеет смысла реализовывать дополнительные затраты на алгоритмизацию.