Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра сопротивления материалов и строительной механики

Сопротивление материалов

Методические указания к выполнению расчетно – графических работ

по курсу «Сопротивление материалов»

Часть 1

Новокузнецк

2013

УДК 620.17

С 64

Рецензент:

кандидат технических наук, доцент,

заведующий кафедрой инженерных конструкций

Н.Н. Алешин

С 64 Сопротивление материалов : метод. указ. / Сиб. гос.

индустр. ун-т ; сост. Ю.А. Епифанцев, А.В. Витушкин.

– Новокузнецк : Изд. центр СибГИУ, 2012. – 69 с.

Представлены задания к выполнению расчетно – графических работ по разделам статически – неопределимых систем, геометрических характеристик плоских сечений, внутренних усилий и напряжений при поперечном изгибе по курсу «Сопротивление материалов». Приведены примеры решения задач и вопросы по выполненным темам.

Предназначены для студентов направления подготовки 270800 Строительство.

Предисловие

Сопротивление материалов – наука о прочности, жесткости и устойчивости отдельных элементов конструкций.

Инженеру строительной специальности часто приходится проводить расчеты элементов конструкций на прочность, то есть на их способность сопротивляться разрушению под действием приложенных к ним внешних нагрузок. Для успешного освоения данного раздела необходимо иметь твердые навыки в решении конкретных задач.

В методические указания включены задания по разделам статически – неопределимых систем, геометрических характеристик плоских сечений, внутренних усилий и напряжений при поперечном изгибе.

Каждый студент согласно учебному плану, в третьем семестре выполняет четыре расчетно – графические работы (РГР). Работы выполняются на бумаге формата А3 (297×420). Штамп вычерчивается по форме, приведенной в таблице 1.

Таблица 1 – Форма штампа

Название темы			Номер схемы _________ Вариант _____________
Кафедра сопротивления материалов и строительной механики			СибГИУ гр.
Выполнил	(подпись)	Ф.И.О.
Принял	(подпись)	Ф.И.О.

РГР №1 – Расчет статически неопределимой системы

Задание. Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стержням с помощью шарниров (расчетные схемы приведены на рисунке 1). Расстояние от бруса до опор в вертикальном направлении = 2 м, a = 1 м. Проверить стержни на прочность при [] = 160МПа.

Задача 1. Расчет системы при действии внешней силы

Вертикальная сила F = 120 кН, направленная вниз, приложена в правом крайнем шарнире бруса (на схеме не показана). Площади поперечного сечения стальных стержней соответственно равны А₁ = 12·10^–4 м², А₂ = 2·10^–3 м².

Рисунок 1 – Расчетные схемы шарнирно – стержневых систем

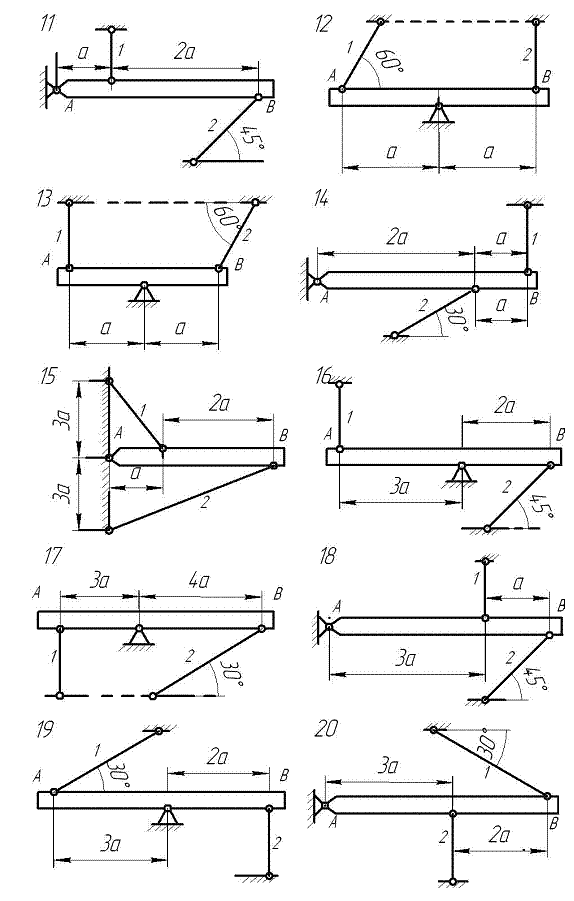
Рисунок 1 – Расчетные схемы шарнирно – стержневых систем

(продолжение)

Рисунок 1 – Расчетные схемы шарнирно – стержневых систем

(продолжение)

Пример решения. Рассмотрим шарнирно – стержневую систему, представленную на рисунке 2.

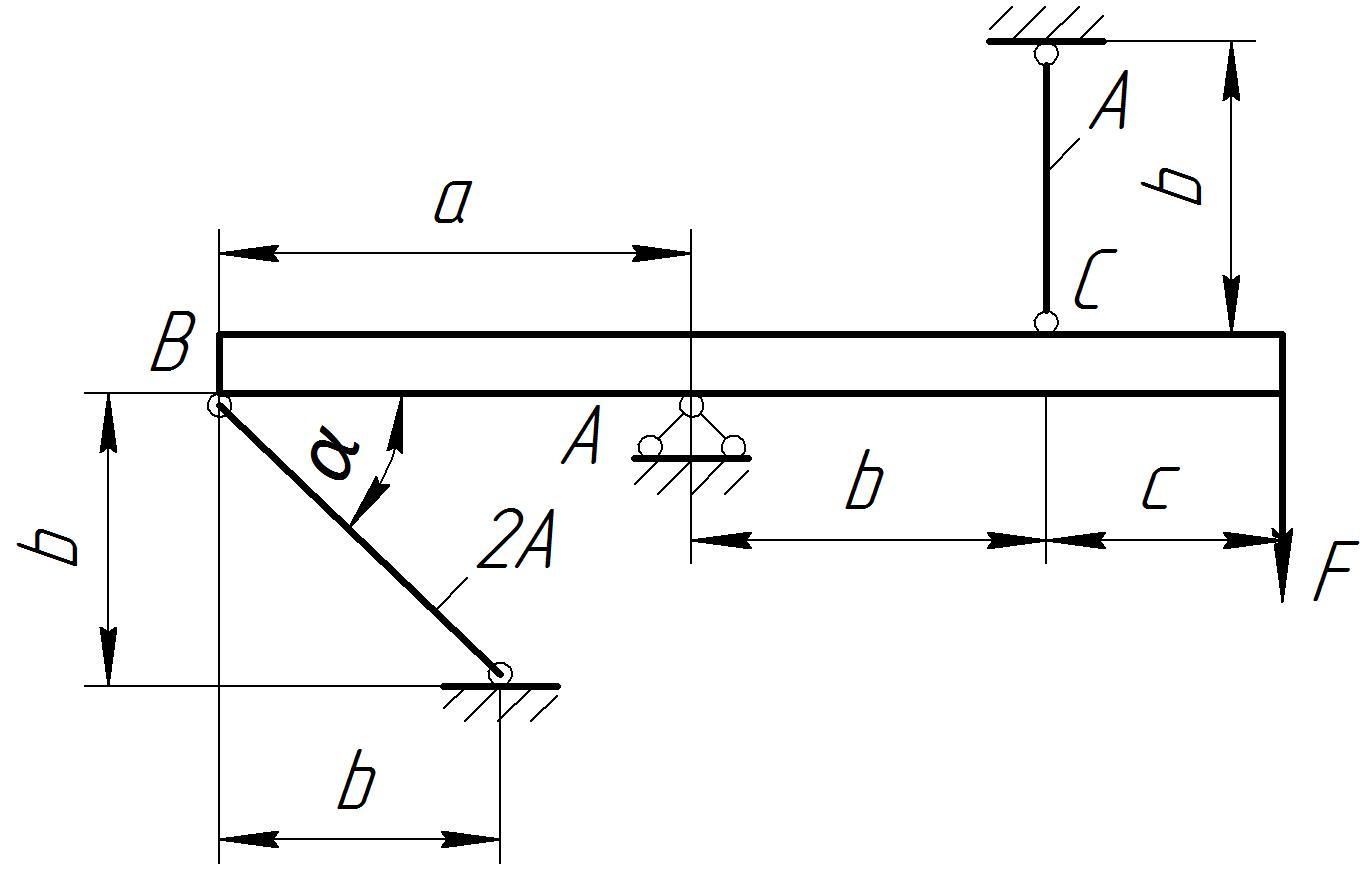
Рисунок 2 – Схема шарнирно – стержневой системы

Данные для расчета:

а = 4 м; в = 3 м; с = 2 м; A = 10м²; α = 45˚; = 160МПа.

Решение

Для определения напряжений от действия внешней нагрузки в деформируемых стержнях 1 и 2 необходимо знать внутренние усилия в этих стержнях Nи N, которые направлены вдоль стержней (рисунок 3). При этом их направления выбираем по правилу: если стержень получает удлинение, то усилие в нем направляем от бруса, и, наоборот, если стержень укорачивается, то к брусу.

От действия заданной нагрузки F в неподвижном шарнире А возникают реактивные силы Vи Н. Для определения усилий в стержнях рассмотрим условия статического равновесия данной системы.

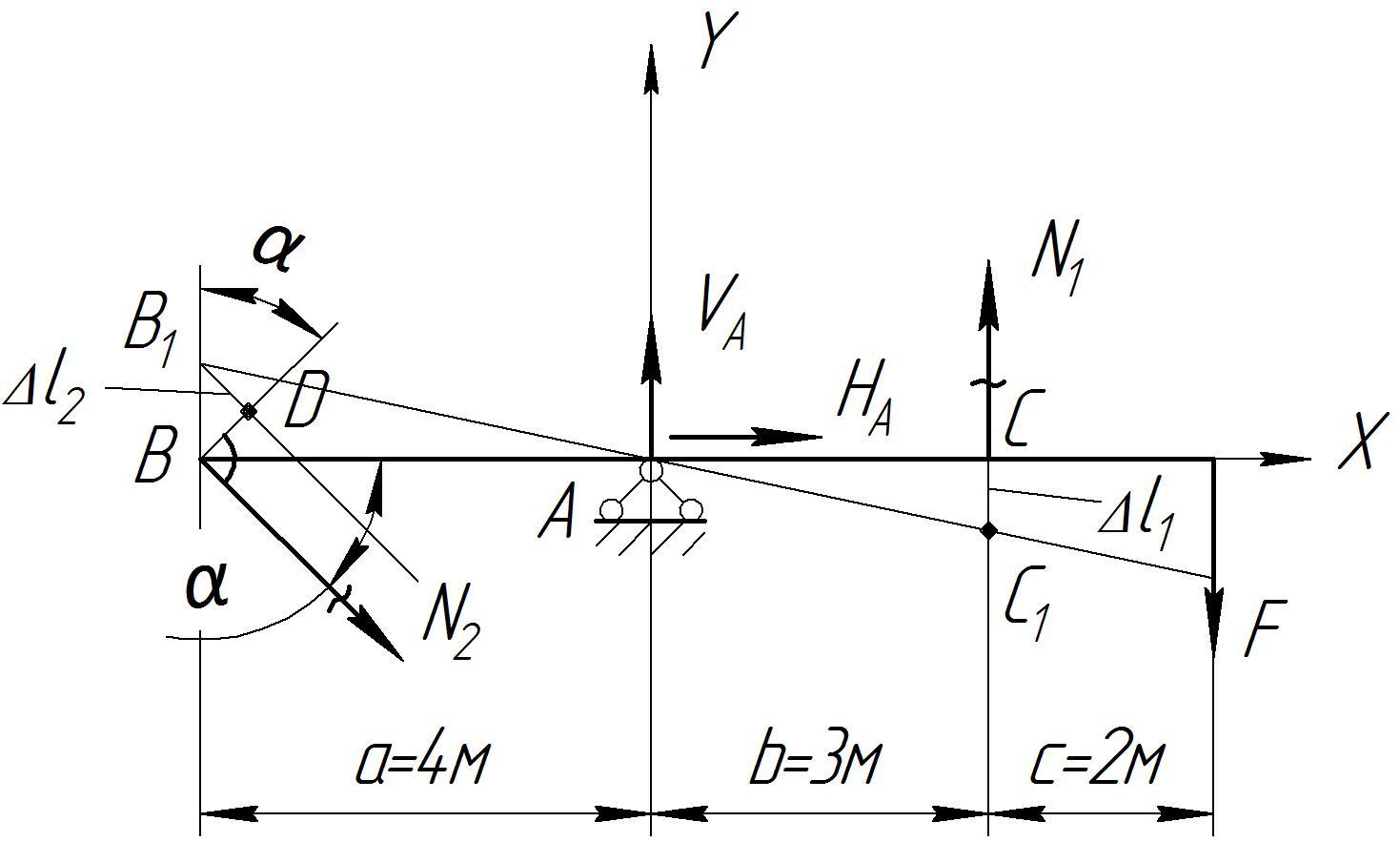
Рисунок 3 – Схема к определению усилий в стержнях

Статическая сторона задачи

Приведем уравнения статического равновесия стержня ВАС. Поскольку система плоская, составим три уравнения:

; НNcos= 0; (1)

; V+ N– NsinF = 0; (2)

; Nв + Na sin – F(c+в) = 0. (3)

В этих трех уравнениях имеется четыре неизвестных усилия. Поскольку величины опорных реакций Vи Нпо условию задачи определять не требуется, то для дальнейшего решения задачи пользуемся уравнением (3). В этом уравнении два неизвестных, таким образом, задача один раз статически неопределима. Дополнительное уравнение составляем из условия совместности перемещений, т.е. геометрической зависимости между деформациями стержней.

Геометрическая сторона задачи

Под действием силы F брус ВАС повернется и займет положение ВАС(рисунок 3), при этом точкаС перейдет в положение С, а точка В – в положение В, перемещаясь по нормали к первоначальному положению бруса ВАС вследствие малости угла поворота. Тогда отрезок СС является удлинением стержня 1. Чтобы найти величину удлинения стержня 2, необходимо на направление стержня 2 из точки В опустить перпендикуляр. Отрезок В₁D представляет собой удлинение стержня 2. Таким образом,

СС= ∆,В₁D = ∆.

Установим зависимость между величинами ∆и ∆. Из подобия треугольниковАВВ и АСС можно записать:

,

где (из ∆BBD).

Тогда

, или .

Следовательно, . (4)

Уравнение (4) представляет зависимость между удлинениями стержней системы.

Физическая сторона задачи

Удлинения стержней 1 и 2 выражаем через усилия NиN по закону Гука:

; .

Тогда выражение (4) запишем так:

в.

Зная, что в и ,

получаем

и затем