Билет 26. Эргодические и поглощающие цепи

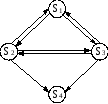
Все множество состояний системы можно разбить на подмножества сообщающихся состояний. Эти подмножества находятся в иерархической зависимости между собой, которая отражает динамику переходов состояний системы в течение времени.

Самое низшее подмножество состояний называется эргодическим множеством. Остальные подмножества называются невозвратными.

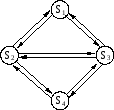
В частном случае эргодическое множество может состоять из одного состояния, которое называется поглощающим.

В соответствии с таким разделением различают эргодические и поглощающие цепи Маркова.

Эргодические цепи Маркова

Для этих цепей характерно то, что при достаточно большом количестве шагов k наступает стационарный режим, при котором P_i(k) независимы от времени и равны P_i. Вектор (P_i)_n – вектор финальных стационарных вероятностей. До наступления стационарного режима имеет место переходной режим, длительность которого можно определить задавшись величиной _i=|P_i -P_i(k)|, если _i>_доп – условие наступления стационарного процесса.

Каждая компонента P_i характеризует среднюю долю времени, в течение которого система находилась в состоянии S_i.

Условием эргодичности однородной Марковской цепи является то, что все ее состояния являются сообщающимися, а граф системы сильно связан (возможен переход S_iS_j за конечное число шагов).

Для определения стационарных вероятностей нужно составить систему из n алгебраических уравнений:

P_i = 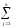P_j*P_ji , i=1, n, (6.15)

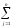P_j = 1. (6.16)

В левой части – вероятности состояния соответствующие рассматриваемым вершинам графа.

В правой части – сумма произведений, число слагаемых равно числу дуг. Слагаемое – произведение вероятности того состояния, из которого выходит дуга, на вероятность соответствующего перехода.

P₁ = P₂P₂₁ + P₃P₃₁

P₁ = P₂P₂₁ + P₃P₃₁

(6.17)

P₁ = P₂P₂₁ + P₃P₃₁

P₁ + P₂ + ... + P_n = 1

Поглощающие цепи Маркова

Поглощающие цепи характеризуются тем, что их эргодическое состояние является поглощающим. В установившемся режиме независимо от начального состояния вероятность нахождения такой Марковской цепи в поглощающем состоянии равна 1, а вероятности всех остальных близки к нулю. В этой связи в поглощающих Марковских цепях интерес представляет переходный процесс в отличие от эргодических, где интерес – установившийся режим, так как задачей анализа Марковских цепей является расчет вероятностей нахождения системы в одном из ее состояний в определенный момент времени t.