
В.М. Волков Математика. Программа, контрольные задания и методические указания для студентов заочного факультета специальности 061000 - Государственное и муниципальное управление
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
МАТЕМАТИКА
Программа, контрольные задания и методические указания для студентов заочного факультета специальности 061000 «Государственное и муниципальное управление»
Составители В.М. Волков Е.А. Волкова В.А. Гоголин Е.Н.Грибанов И.А.Ермакова
А.И. Закамалдин
Утверждены на заседании кафедры Протокол № 6 от 21.05.01 Рекомендованы к печати учебно-методической комиссией специальности 061000 Протокол №7 от 28.06.01 Электронная копия находится в
библиотеке главного корпуса КузГТУ
Кемерово 2001
1
Введение
Программа, задания контрольных работ и методические указания составлены в соответствии со стандартами Министерства образования РФ и с учетом особенностей программ Кузбасского государственного технического университета для студентов экономических специальностей, обучающихся по ускоренной форме подготовки. Контрольные работы № 1,2,3 выполняют в первом семестре, № 4,5,6 – во втором. Для выполнения контрольных работ необходимо изучить теоретический материал в соответствии с рекомендуемой литературой и ссылкой на источник, которая указана при разборе заданий. Программа курса по математике является также списком теоретических вопросов, предлагаемых на экзаменах.
Выбирают свой вариант в каждом задании по двум последними цифрами зачетной книжки – числу десятков и числу единиц. К каждой из этих цифр следует прибавить 1. Таким образом, получаются два числа m и n, задающие значения параметров в каждом задании, соответствующих вашему варианту. Например, если последние цифры 25, то m=3, n=6; если последние цифры 09, то m=1, n=10. На титульном листе выполненных по своему варианту контрольных работ следует указать номер зачетной книжки.
ПРОГРАММА
1семестр
1.Линейная алгебра и аналитическая геометрия
1.1.Элементы теории определителей
1.2.Системы линейных уравнений
1.3.Формулы Крамера
1.4.Метод Гаусса
1.5.Линейные операции над матрицами
1.6.Умножение матриц. Обратная матрица
1.7.Решение систем линейных уравнений в матричной форме
1.8.Векторы. Линейные операции над ними
1.9.Линейная независимость векторов. Базис
1.10.Уравнения прямой на плоскости
1.11.Графическое решение систем линейных неравенств
1.12.Прямая и плоскость в пространстве
2.Введение в математический анализ. Дифференциальное исчисление
2
2.1.Предел функции
2.2.Бесконечно малые и бесконечно большие функции
2.3.Способы раскрытия неопределенностей
2.4.Непрерывность и точки разрыва функции
2.5.Асимптоты
2.6.Производная
2.7.Дифференциал
2.8.Правила дифференцирования
2.9.Условия монотонности и существования экстремума функции
2.10.Выпуклость, вогнутость и точки перегиба графика функции
2.11.Исследование поведения функций и построение графиков
3.Функции нескольких переменных
3.1.Частные производные
3.2.Частные дифференциалы и полный дифференциал
3.3.Производная по направлению. Градиент
3.4.Экстремумы функций двух переменных
2семестр
4.Интегральное исчисление. Дифференциальные уравнения
4.1.Неопределенный интеграл, его свойства
4.2.Основные методы интегрирования
4.3.Интегрирование дробно-рациональных функций
4.4.Задачи, приводящие к понятию определенного интеграла
4.5.Определенный интеграл, его свойства
4.6.Формула Ньютона-Лейбница
4.7.Геометрические приложения определенного интеграла
4.8.Несобственные интегралы
4.9.Дифференциальные уравнения. Общее и частное решения
4.10.Дифференциальные уравнения первого порядка
4.11.Линейные уравнения второго порядка с постоянными коэффициентами
5.Теория вероятностей
5.1.Алгебра событий
5.2.Классическое определение вероятности
5.3.Вероятность суммы и произведения событий
5.4.Формула Бернулли
5.5.Дискретные случайные величины. Законы распределения
5.6.Непрерывные случайные величины. Законы распределения
3
5.7. Числовые характеристики случайных величин 6. Элементы математической статистики
6.1.Выборочная и генеральная совокупности
6.2.Точечная оценка параметров распределения генеральных совокупностей
6.3.Интервальная оценка параметров распределения
6.4.Критерий согласия Пирсона
6.5.Парная линейная регрессия
6.6.Коэффициент корреляции
Контрольная работа № 1 Линейная алгебра и аналитическая геометрия
1. Проверить систему линейных уравнений на совместность и решить ее двумя методами: а) методом Гаусса; б) по формулам Крамера
[1, c.4-12, c.18-23].
x + ny + mz = n −m , |
||
|
2x + |
nz = n , |
|
||
|
3x + ny + mz = 3n −m . |
|
|
||
Пример: |
|
|
x −3y + z = 3 , |
|
|
|
2x + y −3z =1, |
|
|
3x + 2 y = 6. |
|
|
Для проверки системы на совместность вычисляем определитель системы, составленный из коэффициентов при неизвестных
|
|
1 |
−3 |
1 |
|
|
|
|
|||||
∆ = |
|
2 |
1 |
−3 |
|
=34. Так как ∆≠0, то система совместна. |
|
|
3 |
2 |
0 |
|
|
Решаем систему методом Гаусса.
|
Из 2-го уравнения вычтем 1-е уравнение, умноженное на 2. Из 3- |
го уравнения вычтем 1-е, умноженное на 3. Получим систему |
|
|
x − 3y + z = 3 , |
|
7 y −5z = −5 , |
|
|
|
11y − 3z = −3. |
|
|
4
Исключаем y из 3-го уравнения. Для этого 2-е уравнение умножим на 11, 3-е – на 7 и вычтем из 3-го уравнения 2-е. Получим систему
x − 3y + z = 3 , |
|
|
7 y −5z = −5 , |
|
|
|
34z = 34 . |
|
|
В обратном порядке находим из 3-го уравнения z = 1, затем из 2- го уравнения y = 0 и из 1-го уравнения х = 2.
Решение системы: x = 2, y = 0, z = 1. Решаем систему по формулам Крамера.
Определитель системы ∆=34. Вычисляем дополнительные определители, полученные заменой каждого из столбцов определителя системы столбцом правых частей:
|
|
|
|
3 |
−3 |
1 |
|
|
|||||||
|
|
|
|||||||||||||
∆x = |
|
|
1 |
1 |
−3 |
|
= 54 + 2 −6 +18 = 68, |
||||||||
|
|
|
|
6 |
2 |
0 |
|
|
|||||||
|
|
|
|
1 |
3 |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|||||||||||
∆y = |
|
2 1 |
−3 |
|
= −27 +12 −3 +18 = 0, |
||||||||||
|
|
|
|
3 |
6 |
|
0 |
|
|
|
|
|
|
||
∆z = |
|
1 |
−3 |
3 |
|
= 6 −9 +12 −9 −2 +36 = 34. |
|||||||||
|
|
||||||||||||||
|
2 |
1 |
|
1 |
|
||||||||||
|
|
3 |
2 |
6 |
|
|
|
|
|
|
|||||
Находим решение по формулам Крамера:
x = ∆x / ∆ = 68 / 34 = 2,
y = ∆y / ∆ = 0 / 34 = 0,
z = ∆z / ∆ = 34 / 34 =1.
2.Элемент aij матрицы А равен номинальному месячному окладу
i- го работника в j – й месяц. Элемент bij матрицы В равен авансу, выдаваемому i – му работнику в j – й месяц. Районный коэффициент равен K. Найти матрицу окончательных выплат С [1, c.12-17].
1+ m / 5 1+ n / 5 |
||
|
+ m / 4 |
1+ n / 4 |
А= 1 |
||
|
+ m / 3 |
1+ n / 3 |
1 |
||
K=1+m/20.
(n + m) / 5 |
m / 5 |
n / 5 |
m / 5 |
|
||
(n + m) / 4 |
|
|
0 |
n / 4 |
|
, |
, |
В = m / 4 |
|
||||
(n + m) / 3 |
|
|
|
m / 3 |
|
|
|
m / 3 n / 3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
Пример. |
|
|
|
|
|
|
|||
|
3 |
5 |
2 |
|
|
|
1 |
2 |
0 |
|
|
|
2 |
4 |
3 |
|
, |
|
0 |
1 |
1 |
|
К=1,3. |
А= |
|
В= |
, |
||||||||
|
4 |
5 |
6 |
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
||||||
Матрица окончательных выплат находится из матричного уравнения:
|
|
3 |
5 2 |
1 |
2 |
0 |
1,3 3 −1 1,3 5 −2 1,3 2 |
−0 |
|
|||||||
|
|
|
2 |
4 3 |
|
|
0 |
1 |
1 |
|
|
2 |
−0 1,3 4 −1 1,3 3 |
−1 |
|
= |
С=КА–В=1,3 |
|
− |
|
= 1,3 |
|
|||||||||||
|
|
|
4 |
6 5 |
|
|
2 |
2 |
1 |
|
|
4 |
−2 1,3 6 −2 1,3 5 |
−1 |
|
|
|
|
|
|
|
|
1,3 |
|
|
||||||||
2,9 |
4,5 2,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2,6 |
4,2 2,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3,2 |
5,8 5,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Заданы матрица прямых затрат А и товарный вектор b для экономической системы из двух предприятий. Определите вектор плана
[1, c.17-18].
M / 20 |
0,35 |
|
, |
b |
|
2m +3n |
|||
A = |
|
|
|
|
|
= |
. |
||
|
0,2 |
|
N / 20 |
|
|
|
|
|
|
|
|
|
|
|
|
3m + 2m. |
|||
|
Пример. |
|
|
11 |
|
|
|||
|
0,2 |
0,4 |
|
b = |
|
|
|||
A = |
|
|
, |
|
. |
|
|
||
|
0,1 |
0,6 |
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
0,2 |
|
0,4 |
|
|
|
0,8 |
−0,4 |
|
Находим матрицу Е – А = |
|
|
− |
|
|
|
= |
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0,1 |
|
0,6 |
|
|
|
−0,1 |
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычисляем определитель этой матрицы |
|
|
|
|
|
|
|
|
|||||||||||||||
∆ = |
|
0,8 |
|
−0,4 |
|
|
= 0,28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
−0,1 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Строим обратную матрицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
( Е – А ) |
-1 |
|
1 |
|
|
0,4 |
0,4 |
|
1,43 |
1,43 |
|
|
|
|
|
|
|||||||
|
= |
|
|
|
|
× |
0,8 |
≈ |
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
0,28 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0,1 |
|
0,36 |
2,86 |
|
|
|
|
|
|
|||||||||
Находим вектор плана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
X =(E − |
|
|
|
|
|
1,43 1,43 |
|
|
11 |
|
42,9 |
|
|
|
|
||||||||
A)−1 ×b = |
|
|
× |
= |
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,36 |
2,86 |
|
19 |
|
|
|
|
|
|
|||||
6
4. Построить на плоскости область, соответствующую системе неравенств [1, c.46-51].
mx + ny |
|
|
≤ mn , |
|||
(m − n)x + (−1)n y ≤ m − n , |
||||||
|
|
|
|
|
|
|
|
(−1) |
n |
x + (−1) |
m |
my |
≤ 0 . |
|
|
|
||||
|
Пример: |
|
|
|
||
|
2х + у ≤10 , |
|
||||
|
|
х + 3у ≤15 , |
|
|||
|
|
|
||||
|
|
х + у ≥ 0 . |
|
|
||
|
|
|
|
|||
Строим прямые, являющиеся границами области:
2х + у = 10, |
х + 3у = 15, |
х + у = 0. |
||||
х 0 5 |
х 0 15 |
х 0 5 |
||||
|
|
|
|
|
|
|
у 10 0 |
у 5 0 |
у 0 -5 |
||||
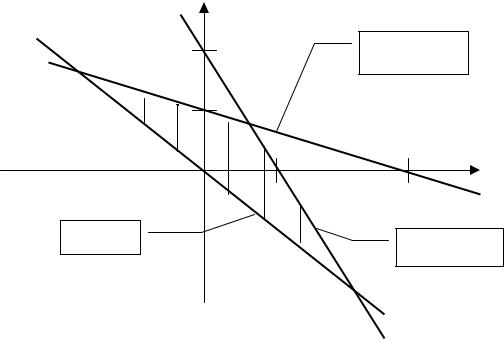
Выделяем части плоскости (полуплоскости), которые соответствуют знакам неравенств. Для этого подставляем координаты произвольной точки в неравенства и проверяем их знак. Так для точки О(0;0) 1-е и 2-е неравенства выполняются, поэтому все точки плоскости, лежащие по одну сторону от прямых вместе с точкой О, являются решением 2-х первых неравенств. Выполнение третьего неравенства нельзя проверить координатами точки О, т.к. получаем 0=0. Выбираем другую точку, например (0;5). Для него 3-е неравенство выполняется. Поэтому соответствующая полуплоскость лежит выше 3-й прямой. Находим пересечение полуплоскостей и получаем область, соответствующую системе неравенств (на рисунке она заштрихована).
|
y |
|
|
10 |
|
x+3y=15 |
|
5 |
|
|
|
0 |
5 |
15 |
x |
|
|||
x+y=0 |
|
2x+y=10 |
|
|
|
|
7
Контрольная работа № 2 Введение в математический анализ Дифференциальное исчисление
|
1. Найти пределы [1,68-77]. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
а) |
lim |
(m |
−2n)x3 + nx2 +(m −n) x |
, |
|
|
|
|
|
|
|
||||||||||||
|
|
m + nx − |
(2m −n)x3 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) |
lim |
x3 |
−nx2 −( −1)m mx +( −1)m nm |
, |
|
|
|
|
|
|
|||||||||||||
|
|
x2 +( m −n )x −mn |
|
|
|
|
|
|
|
|
|
||||||||||||
|
x→n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) |
lim |
ln(1+( −1)n |
|
2mxn −nxm ) |
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
nxn + mxm |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a) lim |
2x |
3 −4x 2 +1 |
= |
|
∞ |
2x 3 |
|
−4x 2 +1 ~ 2x 3 |
, 3 −2x − x 3 ~ −x 3 = |
||||||||||||||
|
−2x − x 3 |
|
|
= |
|
||||||||||||||||||
|
x→∞ 3 |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
lim |
2x |
3 |
= −2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
− x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 −4 |
|
|
|
|
0 |
|
|
( x − |
2 )( x + 2 ) |
|
|
|
x + 2 |
|
|||||||
б) |
lim |
|
|
|
|
|
= |
|
|
= lim |
( x − |
|
2 )( x −1) |
= lim |
|
|
|
= 4. |
|||||
|
− |
3x − |
2 |
|
|
|
x −1 |
||||||||||||||||
|
x→2 x2 |
|
|
0 |
|
x→2 |
|
x→2 |
|
|
|||||||||||||
в) |
lim |
ln(1− x3 ) |
= |
|
0 |
= |
ln(1− x3 ) ~ −x3 = lim |
− x3 |
= − lim x = 0. |
||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|||||||||||||||
|
x→0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x→0 x2 |
|
x→0 |
||||||
|
2. Найдите точки разрыва функции. Сделайте чертеж [1, c.77-81]. |
||||||||||||||||||||||
|
|
|
|
|
|
(−1)m mx2 , x ≤ 0, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
y = |
(−1)n nx +(−1)n +(−1)m ,0 p x ≤ m, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−1) |
m |
/(m − x), x f m. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x2 ,x ≤ 0; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
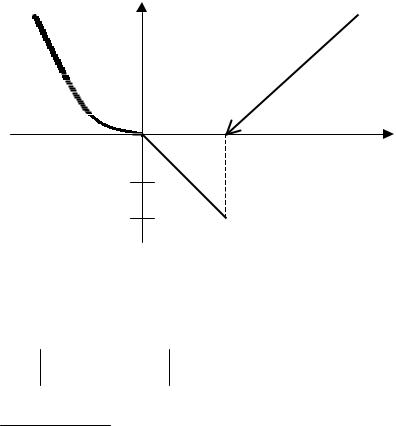
Пример: y = −2x,0 p x ≤ 4; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x −4,x f 4. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
На интервалах (–∞;0), (0;4), (4;+∞) функция непрерывна. Исследуем поведение функции в точках х=0 и х=4.
lim |
y = |
lim |
3x2 = 0 = y( 0 ). |
lim y = lim −2x = 0. |
|
x→0−0 |
|
x→0−0 |
x→0+0 |
x→0+0 |
|
В точке х=0 функция непрерывна. |
|
||||
lim |
y = |
lim |
−2x = −8 = y( 4 ). |
lim |
y = lim x −4 = 0. |
x→4−0 |
|
x→4−0 |
|
x→4+0 |
x→4+0 |
В точке х=4 функция имеет разрыв 1-го рода.
y |
|
|
0 |
4 |
x |
- 4 |
|
|
- 8 |
|
|
3.Исследуйте поведение функций и постройте их графики [1, c.81100].
y =( −1)n xn+2 +( −1)m( n +2 )xк / k +( n −m ), а) k =1+ 12 ( −1)m +( −1)n ,
б) y = ( −1)m x2 + n . ( −1)n xк −m
Примеры: а) у=5х4-4х5+1. Область определения функции (–∞;+∞).
lim y = |
lim ( 5x4 −4x5 +1) = |
lim ( −4x5 ) = m∞. |
|
||
x→±∞ |
x→±∞ |
|
x→±∞ |
|
|
Функция непрерывна. Вертикальных асимптот нет. |
|
||||
Находим наклонные асимптоты у=kх+b. |
|
||||
k = lim |
y |
= lim |
5x4 −4x5 +1 = |
lim ( 5x3 −4x4 +1 / x ) = lim −4x4 = −∞. |
|
|
|||||
x→∞ x |
x→∞ |
x |
x→∞ |
x→∞ |
|
Следовательно, наклонных асимптот нет.
Устанавливаем области монотонности и находим экстремумы функции:

9
у′=20х3-20х4=0, х3-х4=0, х3(1-х)=0.
х1=0, х2=1 – критические точки на экстремум.
Определяем знаки производной на интервалах и соответственно
области монотонности: |
|
|
|
|
|
y′ |
– |
• |
+ |
• |
– |
|
|||||
y |
убыв. |
0 |
возр. |
1 |
убыв. x |
Таким образом, ymin( 0 ) =1, ymax(1) = 2.
Исследуем график функции на выпуклость, вогнутость и найдем точки перегиба: y′′=(20x3–20x4)′=60x2–80x3=0,
3х2 – 4х3 = 0; х1 = 0, х2 = 3/4 – критические точки на перегиб. Определяем знаки второй производной на интервалах, а по ним -
области выпуклости и вогнутости графика:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||
|
вогн. |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
вогн. |
3/4 |
|
|
|
|
|
|
|
|
|
вып. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таким образом, х2 =3/4 – точка перегиба, |
|
у(3/4) = 1,6. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Составляем таблицу характерных точек функции и по ней строим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ее график: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
х |
|
|
|
|
|
|
|
|
-∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/4 |
|
|
|
|
|
|
|
|
|
1 |
+∞ |
||||||||||||||||||||||||||||||||||
|
у |
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,6 |
|
|
|
|
|
|
|
|
|
2 |
-∞ |
|||||||||||||||||||||||||||||||||||
• |
|
|
y |
|
|
|
|
|
|
|
|
(+∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
1 |
• |
|
|
∞ |
|
x |
(– |
) |
0 |
3/4 |
1 |
(+ |
) |
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
(– ∞) |
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
