
- •Министерство Образования и науки Российской Федерации
- •Основы теории обработки результатов.
- •Погрешности измерения.
- •Модуль 1. Механика Лабораторная работа №2 «Определение ускорения свободного падения»
- •Краткая теория
- •2. Описание установки. Порядок выполнения работы.
- •Протокол лабораторной работы №2.
- •Список рекомендуемой литературы
- •Описание установки
- •3. Порядок выполнения работы а. Проверка правильности соотношения
- •Б. Проверка правильности соотношения
- •Вопросы для самопроверки к работе №3
- •2. Порядок выполнения работы.
- •Протокол лабораторной работы №4.
- •2.Описание установки
- •3. Порядок выполнения работы
- •Протокол лабораторной работы №5
- •Понятие температуры
- •Уравнение Клапейрона–Менделеева и изопроцессы
- •2. Описание прибора
- •3. Порядок выполнения работы
- •Протокол лабораторной работы №6.
- •Вопросы для самопроверки к работе №6
- •Список рекомендуемой литературы
- •1. Описание установки.
- •1. Порядок выполнения работы
- •Протокол лабораторной работы №7
- •Вопросы для самопроверки к работе №7
- •2. Порядок выполнения работы.
- •Протокол лабораторной работы №8
- •Вопросы для самопроверки к работе №8
- •Порядок выполнения работы.
- •Данные установки
- •Протокол лабораторной работы №9
- •Обработка результатов измерений
- •Прилагается к данной работе:
- •Порядок выполнения работы
- •Данные установки
- •Протокол лабораторной работы №10
- •Обработка результатов измерений
- •Вопросы для самопроверки к работе №10
- •Описание аппаратуры и порядок выполнения работы
- •Вопросы для самопроверки к работе №11
- •Порядок выполнения работы.
- •Описание метода измерения и установки.
- •Порядок выполнения работы.
- •Протокол лабораторной работы №15
- •Вопросы для самопроверки к работе №15
- •Принцип Гюйгенса
- •Принцип Гюйгенса – Френеля
- •Метод зон Френеля
- •Дифракция от щели в параллельных лучах
- •Дифракционная решетка
- •Лабораторная установка и порядок проведения работы
- •Часть I
- •Часть II
- •Протокол лабораторной работы №24
- •Вопросы для самопроверки к работе №24
- •Поляризация при отражении и преломлении
- •Поляризация при двойном лучепреломлением
- •Поляризационная призма Николя
- •Закон Малюса
- •Порядок выполнения работы
- •Протокол лабораторной работы №25
- •Внешний фотоэффект, законы Столетова.
- •Внешний фотоэффект и волновая теория света
- •Уравнение Эйнштейна для внешнего фотоэффекта
- •Внутренний фотоэффект
- •Типы фотоэлементов
- •Порядок выполнения работы
- •Протокол лабораторной работы №28
- •Вопросы для самопроверки к работе №28
- •Дисперсия света
- •Сериальные формулы
- •Ядерная модель строения атома по Резерфорду
- •Затруднения теории Резерфорда
- •Понятие о квантах и постоянная Планка
- •Постулаты Бора
- •Волны де Бройля
- •Линейчатые спектры по теории Бора
- •Энергетические уровни в атоме
- •Вывод расчетной формулы
- •Описание установки и порядок выполнения работы
- •Порядок выполнения работы
- •Протокол лабораторной работы №26
- •Протокол лабораторной работы №30 Вопросы для самопроверки к работе №30 Список рекомендуемой литературы
- •Правила оформления результатов выполнения заданий по каждой работе Лабораторного практикума
Обработка результатов измерений
Определить по ртутному термометру температуру воздуха к лаборатории и принять её равной температуре воздуха на входе в калориметр Твх.
По табл. 2 определить термо–ЭДС Евх хромель алюминевой термопары, соответствующую Твх.
Прибавляя к каждому измеренному значению
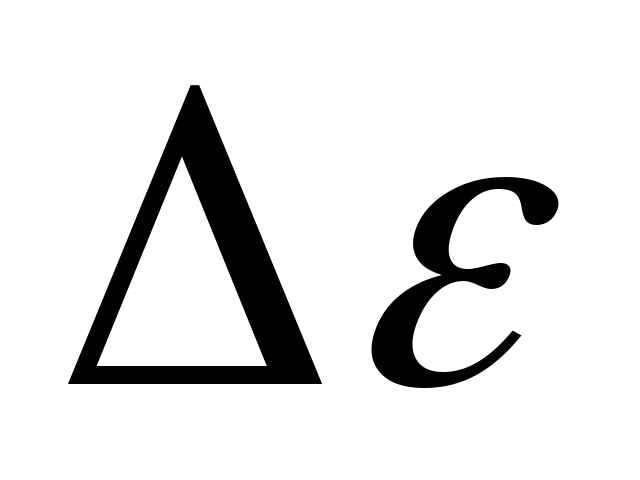 ,
значениеЕвх,
определить по табл. 2 температуру
воздуха на выходе из калориметра
Твых.
,
значениеЕвх,
определить по табл. 2 температуру
воздуха на выходе из калориметра
Твых.Рассчитать разность температур воздуха на выходе и входе калориметра
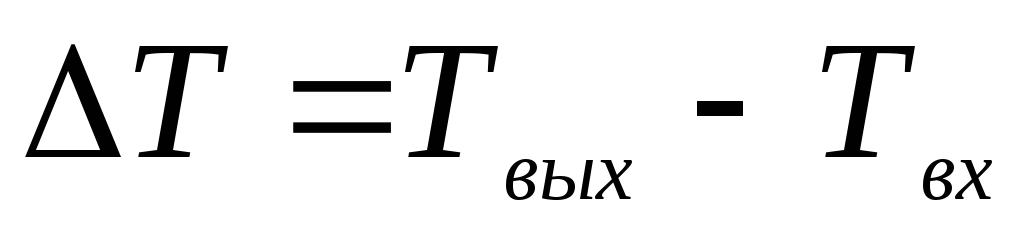 ,
записать полученное значение в табл.
1.
,
записать полученное значение в табл.
1.Рассчитать
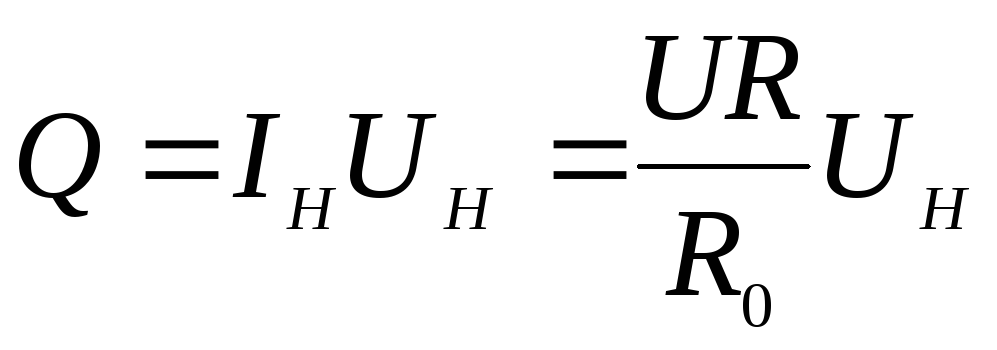 ,
записать полученные значения в табл.
1.
,
записать полученные значения в табл.
1.По полученным данным построить график линейной зависимости
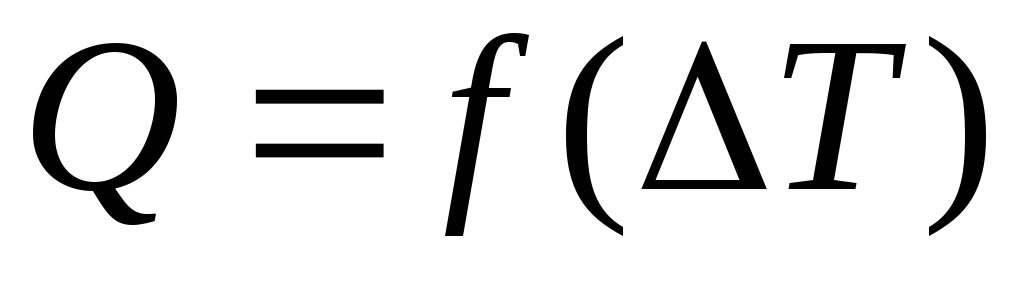 .
.Провести оптимальную прямую через набор экспериментальных точек.
Определить тангенс угла наклона оптимальной прямой по формуле:
![]() (6)
(6)
Рассчитать удельную теплоёмкость воздуха при постоянном давлении
![]() (7)
(7)
Градуированная характеристика хромель–копелевой термопары (по СТ СЭВ 1059–79) (табл. 2).
Прилагается к данной работе:
В качестве данных установки может быть задан массовой расход воздуха, который является постоянным в течении всего опыта.
Вопросы для самопроверки к работе №9
В чём отличие газов от твёрдых и жидких тел? Какими основными параметрами определяется состояние газа?
Какую величину определяют в работе?
Дайте определение теплоёмкостей (удельной, молярной). Что такое
 и
и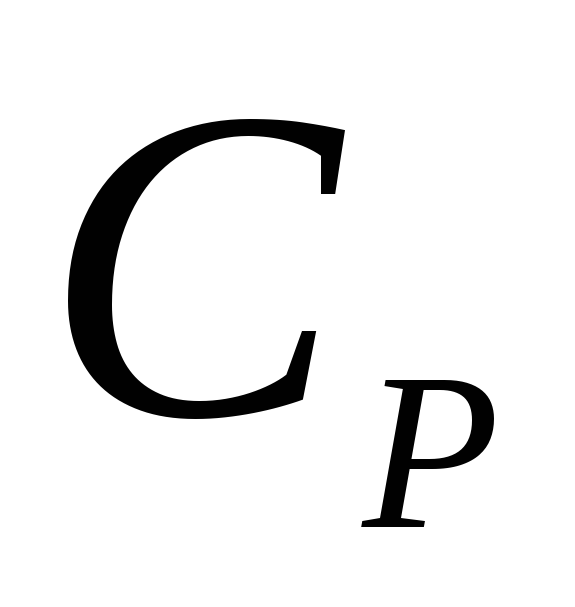 ?
?Напишите уравнение Майера и I начало термодинамики для изобарного процесса.
Список рекомендуемой литературы
1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2009.
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2010.
Материально–техническое обеспечение
Установка для лабораторной работы по молекулярной физике «Определение удельной теплоёмкости воздуха при постоянном давлении»
Лабораторная работа №10.
«Определение коэффициента теплопроводности методом нагретой нити»
1. Краткая теория.
Движение
молекул газа в термодинамической
равновесной системе полностью хаотична.
Из основных представлений кинетической
теории следует, что газы испытывают в
1 секунду порядка
![]() столкновений (соударений). Число
столкновений (среднее) за 1с
столкновений (соударений). Число
столкновений (среднее) за 1с
![]() ,
,
где d – эффективный диаметр молекул газа;
n
– концентрация (т.е. число молекул в
единице объёма);
![]() ;
;
![]() –средняя
арифметическая скорость молекул.
–средняя
арифметическая скорость молекул.
Расстояние,
которое проходит молекула между двумя
последовательными соударениями
называется средней длиной свободного
пробега
![]()
![]() ;
;
В газах и жидкостях вследствие хаотичного движения молекул происходит необратимый процесс переноса различных физических величин. Эти явления объединяются общим названием «явления переноса».
I. Перенос массы от мест с более высокой концентрацией молекул к местам с более низкой концентрацией называют диффузией.
Эта масса определяется уравнением:
![]()
Здесь
![]() – площадка, нормальная к потоку,
продиффундирующему через неё массыМ;
– площадка, нормальная к потоку,
продиффундирующему через неё массыМ;
![]() –время
движения молекул через площадку
–время
движения молекул через площадку
![]() ;
;
![]() –градиент
концентрации;
–градиент
концентрации;
![]() ;
;![]() –
масса молекулы газа;
–
масса молекулы газа;
Д
– коэффициент диффузии:
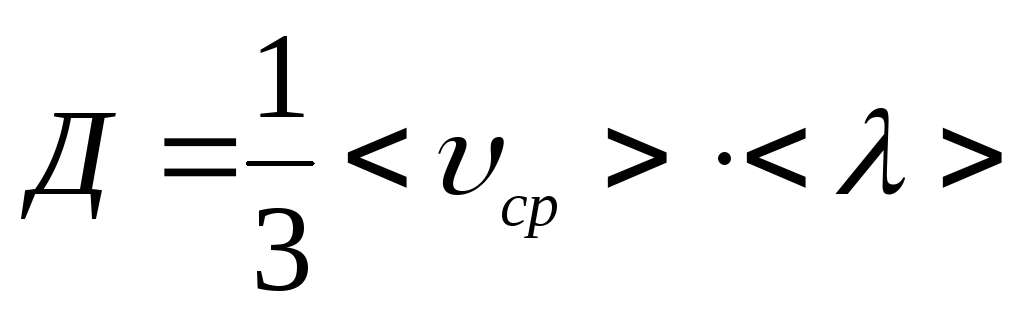 .
.
II.
Перенос энергии происходит вследствие
хаотичного движения молекул из областей
с более высокой температуры и обладающих
большей энергией (![]() )
в области с более низкой температурой.
Этот процесс называетсятеплопроводностью.
Перенос энергии определяется уравнением
)
в области с более низкой температурой.
Этот процесс называетсятеплопроводностью.
Перенос энергии определяется уравнением
![]()
где
Q
– количество теплоты, перенесённое
через изотермическую площадку
![]() за время
за время![]() ;
;
![]() –градиент
температуры;
–градиент
температуры;
х – коэффициент теплопроводности.
![]() ;
;
![]() –удельная
изохорическая теплоёмкость.
–удельная
изохорическая теплоёмкость.
При движении тела в вязкой среде возникает сопротивление этому движению. При малых скоростях и обтекаемой форме тела сопротивления обусловлена вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твёрдому телу, прилипает к его поверхности и увлекается им. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы внутреннего трения.
При падении шарика радиуса r в вязкой жидкости, находящеёся в мензурке (рис. 1), на него действует две противоположно направленные силы. Одна из них f обусловлена гравитацией за вычетом выталкивающих (архимедовой) силы. Другая сила F обусловлена внутренним тернием. Из теории следует, что
![]() (1)
(1)
![]() (2)
(2)
где
![]() – коэффициент вязкости (или внутреннего
трения);
– коэффициент вязкости (или внутреннего
трения);
![]() –плотность
вещества шарика;
–плотность
вещества шарика;
![]() –плотности
жидкости;
–плотности
жидкости;
g – ускорение силы тяжести;
![]() –скорость
шарика.
–скорость
шарика.
Цель работы: Экспериментальное определение коэффициента теплопроводности воздуха, находящегося вокруг нагретой электрическим током нити. В работе определяется электрическая мощность, выделяемая в нити, и температура нити.
Схема модуля №3. схема измерений.
Нагреваемая вольфрамовая проволока – нить находится в цилиндрическом стеклянном баллоне с двойными стенками, между которыми залита вода. Температура воды в баллоне и, следовательно, температура стенки Тс трубки постоянна в течении опыта. Баллон с нитью укреплён в модуле №3, внешний вид которого показан на рис. 4. На панели модуля расположены: 1 – табличка с названием работы; 2 – баллон с нитью; 3 – гнёзда для подключения источника питания; 4 – гнёзда для подключения вольтметра (мультиметра); 5 – тумблер объектов измерения.
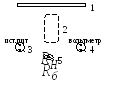
При нагревании нити, вдоль радиуса трубки создаётся градиент температуры. Площадь, через которую передаётся тепло, равна площади поверхности цилиндра, коаксиального с нагретой нитью. При этом можно записать:
![]() (1)
(1)
где l – длина цилиндра радиуса r.
Из
(1) можно определить мощность теплового
потока через внутреннюю цилиндрическую
поверхность трубки радиуса
![]() .
.
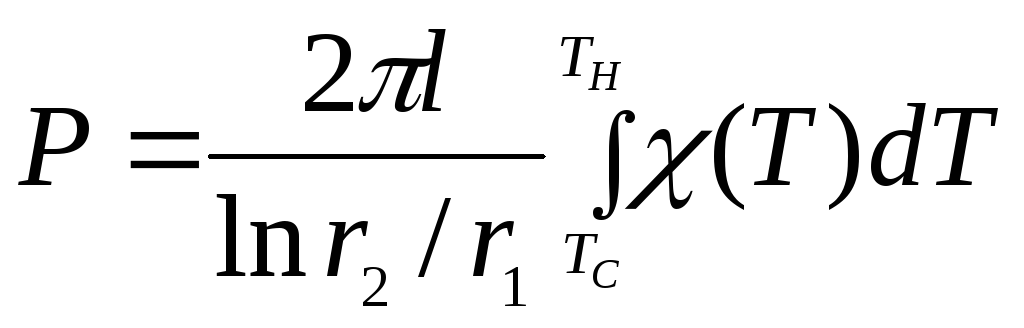 (2)
(2)
где
![]() – радиус нити,ТН
– температура нити.
– радиус нити,ТН
– температура нити.
Опыт проводится при постоянной температуре трубки, равной Тс. При этом увеличение электрической мощности, выделяемой в нить, на величину d Р приводит к возрастанию её температуры на d ТН. Поэтому из (2) следует:
![]() (3)
(3)
Так
как вблизи нити теплопроводность воздуха
определяется температурой нити, то в
(3) величина
![]() (ТН)
относится к температуре нить ТН.
При возрастании температуры нити на d
ТН,
дополнительный перенос тепловой мощности
d
Р
от нити к стенке трубки определяется
только теплопроводностью слоя воздуха
вблизи нити. Из соотношения (3) получим:
(ТН)
относится к температуре нить ТН.
При возрастании температуры нити на d
ТН,
дополнительный перенос тепловой мощности
d
Р
от нити к стенке трубки определяется
только теплопроводностью слоя воздуха
вблизи нити. Из соотношения (3) получим:
![]() (4)
(4)
Для
определения производной необходимо
знать зависимость
![]() ,
которую находят по экспериментальным
данным. Мощность теплового потока
,
которую находят по экспериментальным
данным. Мощность теплового потока![]() находится по напряжению
находится по напряжению![]() ,
измеренному на нити, и току
,
измеренному на нити, и току![]() ,
текущему через образцовое сопротивление
,
текущему через образцовое сопротивление![]() и нить. Для определения тока измеряется
напряжение на образцовом сопротивление
и нить. Для определения тока измеряется
напряжение на образцовом сопротивление![]() .
Температура нити определяется из
соотношения:
.
Температура нити определяется из
соотношения:
![]() (5)
(5)
где
![]() – сопротивление нити при
– сопротивление нити при![]() ,
(Ом);
,
(Ом);![]() – сопротивление нити при температуре
опыта, (Ом);
– сопротивление нити при температуре
опыта, (Ом);![]() – температурный коэффициент сопротивления
материала нити, (1/град.). Формула (4)
позволяет по найденной экспериментальной
зависимости
– температурный коэффициент сопротивления
материала нити, (1/град.). Формула (4)
позволяет по найденной экспериментальной
зависимости![]() определить
определить![]() .
.
Дифференцируя (5) получаем:
![]() (6)
(6)
Подставляя d ТН из (6) в (4), получаем:
![]() (7)
(7)
Формула
(7) позволяет использовать график
зависимости
![]() для нахождения производной
для нахождения производной![]() .
.
