20. Первое начало термодинамики. Изопроцессы.

Первый закон термодинамики: кол-во теплоты, сообщ.системе, расходуется на изм.внутренней энергии тела и на совершение системы работы над внешними телами ∆Q=∆U+∆A. если система возвращается в исходное состояние, то ∆U=0

Нельзя построить периодически действующий двигатель, который совершал бы работу большую подводим.к нему энергии извне dQ=dA

Частные случаи

Рассмотрим несколько частных случаев:

1. Если , то это означает, что тепло к системеподводится.

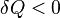2. Если , аналогично — теплоотводится.

3. Если , то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

Cтетради

21. Второе начало термодинамики. Энтропия.второй закон термодинамики: возможны лишь такие процессы в замкнутой макроскопической системе, который приводят к увеличении ее энтропии, т.к. реальные процессы всегда необратимы, то энтропия возрастает. Она является ф-ей состояния системы. Она не зависит от процесса перехода системы из одного состояния в другое.

Энтропия — это сокращение доступной энергии вещества в результате передачи энергии.

С тетради (начало с формул)

22. Цикл Карно. Кпд цикла

В термодинамике цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатическихи двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температуройи рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T(температура) иS(энтропия).

1. Изотермическое расширение(на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение(на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника, тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие(на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты. Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие(на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

КПД тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

23. Основное уравнение МКТ и следствия их него. Распределение Максвелла.  Молекулярно-кинетическая теория(сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

• все тела состоят из частиц: атомов, молекул и ионов;

• частицы находятся в непрерывном хаотическом движении (тепловом);

• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.

МКТ стала одной из самых успешных физических теорий и была подтверждена целым рядом опытных фактов. Основными доказательствами положений МКТ стали:

• Диффузия

• Броуновское движение

• Изменение агрегатных состояний вещества

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).

Упрощенный вывод основного уравнения МКТ

Пусть имеется частиц массойв некотором кубическом сосуде.

Так как молекулы движутся хаотически, то события, состоящие в движении в одном из шести независимых направлений пространства, совпадающих с осями декартовой системы координат, равновероятны.

Поэтому, в каждом из этих направлении движется частиц.

Пусть все частицы обладают одинаковой скоростью .

Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс .

Если площадь стенки , а концентрация -, то количество частиц, сталкивающихся со стенкой за времяравно.

Так как , а- суммарная сила взаимодействия частиц со стенкой, то подставив соответствующие значения получим,

так как , то

Уравнение среднеквадратичной скорости молекулы

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

,

, где — молярная масса газа,— масса молекулы газа.

Отсюда окончательно

Следствия из него: в тетради

Распределение Масквелла( в тетради):