Beginning Algorithms (2006)

Chapter 6

Summar y

Highlights of this chapter include the following:

You implemented three simple sorting algorithms — the bubble sort, the selection sort, and the insertion sort — complete with unit tests to prove they work as expected.

You were introduced to the concept of comparators, and implemented several of them, including the natural comparator, a reverse comparator, and a call counting comparator.

You looked at a comparative investigation of the three algorithms so that you can make informed decisions about the strengths and weaknesses of each.

The idea of stability as it relates to sorting was also discussed.

Having worked through this chapter, you should understand the importance of sorting and the role it plays in supporting other algorithms, such as searching algorithms. In addition, you should understand that there are many ways to achieve the simple task of arranging objects in sequence. The next chapter introduces some more complex sorting algorithms that can sort huge amounts of information amazingly well.

Exercises

1.Write a test to prove that each of the algorithms can sort a randomly generated list of double objects.

2.Write a test to prove that the bubble sort and insertion sort algorithms from this chapter are stable.

3.Write a comparator that can order strings in dictionary order, with uppercase and lowercase letters considered equivalent.

4.Write a driver program to determine how many objects are moved by each algorithm during a sort operation.

144

Chapter 7

lies in repeating this process several times with careful creation of larger and larger sublists, until the whole list is sorted using an insertion sort on the final pass. As you learned in the previous chapter, an insertion sort is very effective on nearly sorted data, and this is exactly the state of the data on the final pass of a shellsort.

This shellsort example sorts the letters shown in Figure 7-1 alphabetically.

B E G I N N I N G A L G O R I T H M S

Figure 7-1: Sample data to demonstrate shellsort.

Shellsort is built upon the concept of H-sorting. A list is said to be H-sorted when, starting at any position, every H-th item is in sorted position relative to the other items. That concept will become clear as you work through an example. In the following Try It Out, you start by 4-sorting the list from Figure 7-1. In other words, you will consider only every fourth element and sort those items relative to each other.

Figure 7-2 shows every fourth item starting at position 0.

B E G I N N I N G A L G O R I T H M S

Figure 7-2: Every fourth item starting at position 0.

Ignoring all other items, you sort the highlighted items relative to each other, resulting in the list shown in Figure 7-3. The highlighted items now appear in alphabetical order (B, G, H, N, O).

B E G I G N I N H A L G N R I T O M S

Figure 7-3: Every fourth item starting at position 0 sorted relative to each other.

You now consider every fourth item starting at position 1. Figure 7-4 shows these items before and after they are sorted relative to each other.

Figure 7-4: Sorting every fourth item starting at position 1.

Next you 4-sort starting at position 2, as shown in Figure 7-5.

146

Advanced Sorting

Figure 7-5: Sorting every fourth item starting at position 2.

Finally, you consider every fourth item starting at position 3. Figure 7-6 shows the situation before and after this step.

Figure 7-6: Sorting every fourth item starting at position 3.

There is no more to do to 4-sort the sample list. If you were to move to position 4, then you would be considering the same set of objects as when you started at position 0. As you can see from the second line in Figure 7-6, the list is by no means sorted, but it is 4-sorted. You can test this by choosing any item in the list and verifying that it is less than (or equal to) the item four positions to its right, and greater than (or equal to) the item four positions to its left.

The shellsort moves items a long way quickly. For very large lists of items, a good shellsort would start with a very large value of H, so it might start by 10,000-sorting the list, thereby moving items many thousands of positions at a time, in an effort to get them closer to their final sorted position quickly. Once the list is H-sorted for a large value of H, shellsort then chooses a smaller value for H and does the whole thing again. This process continues until the value of H is 1, and the whole list is sorted on the final pass. In this example, you 3-sort the list for the next pass.

Figure 7-7 shows every third item starting at position 0, both before and after being sorted relative to each other. By the way, notice the arrangement of the last four letters!

Figure 7-7: 3-sorting at position 0.

You move to position 1, and by coincidence there is nothing to do, as shown in Figure 7-8.

147

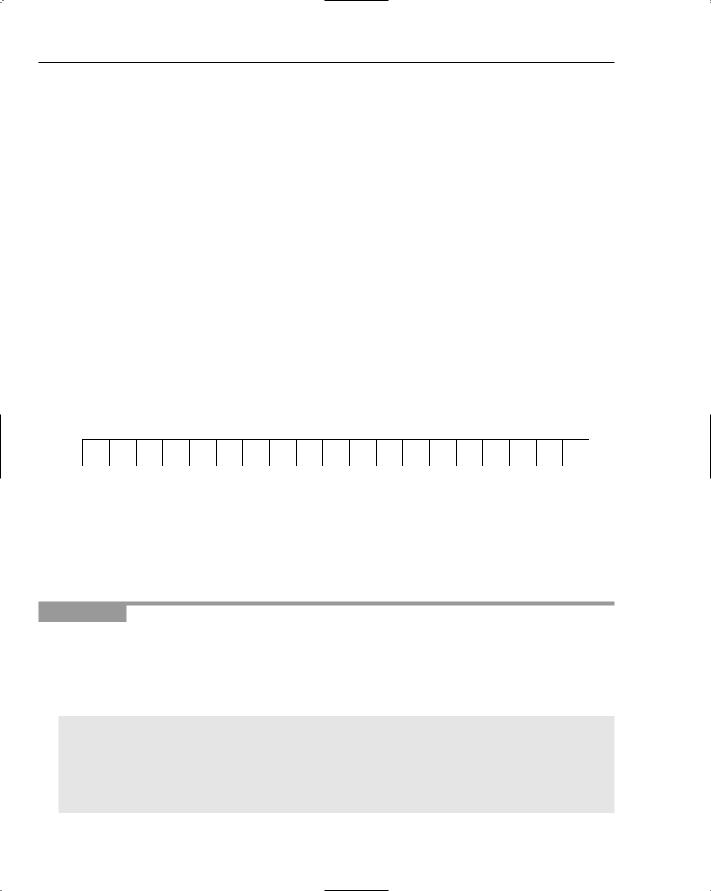
Chapter 7

Figure 7-8: 3-sorting at position 1.

Finally, you sort every third item starting at position 2, as shown in Figure 7-9.

Figure 7-9: 3-sorting at position 2.

Notice how the list is now nearly sorted. Most items are only a position or two away from where they should be, which you can accomplish with a simple insertion sort. After a quick run over the list, you end up with the final sorted arrangement shown in Figure 7-10. If you compare this with the previous list, you will see that no item had to move more than two positions to reach its final position.

A B E G G G H I I I L M N N N O R S T

Figure 7-10: The final sorted list.

Much of the research into shellsort has revolved around the choice of the successive values for H. The original sequence suggested by the algorithm’s inventor (1, 2, 4, 8, 16, 32, . . .) is provably terrible, as it compares only items in odd positions with items in odd positions until the final pass. Shellsort works well when each item is sorted relative to different items on each pass. A simple and effective sequence is (1, 4, 13, 40, . . .) whereby each value of H = 3 × H + 1. In the following Try It Out, you implement a shellsort.

In this section, you will implement the shellsort algorithm, using the same test data you used to drive the sorting algorithms in the previous chapter.

The test for your shellsort algorithm should look familiar by now. It simply extends AbstractListSorterTest and instantiates the (not yet written) shellsort implementation:

package com.wrox.algorithms.sorting;

public class ShellsortListSorterTest extends AbstractListSorterTest { protected ListSorter createListSorter(Comparator comparator) {

return new ShellsortListSorter(comparator);

}

}

148

Advanced Sorting

How It Works

The preceding test extends the general-purpose test for sorting algorithms you created in Chapter 6. All you need to do to test the shellsort implementation is instantiate it by overriding the createListSorter() method.

In the following Try It Out, you implement the shellsort.

The implementation has a similar structure to those for the basic sorting algorithms. It implements the ListSorter interface, and requires a comparator to impose the order on the items. Create the implementation class with an instance field to hold the comparator to be used, and an array of integers representing the H-values to be used:

package com.wrox.algorithms.sorting;

import com.wrox.algorithms.lists.List;

public class ShellsortListSorter implements ListSorter { private final Comparator _comparator;

private final int[] _increments = {121, 40, 13, 4, 1};

public ShellsortListSorter(Comparator comparator) {

assert comparator != null : “comparator cannot be null”; _comparator = comparator;

}

...

}

The sort() method, which you create next, simply loops through the increments defined in the previous array and calls hSort() on the list for each increment. Note that this relies on the final increment having a value of 1. Feel free to experiment with other sequences, but remember that the final value has to be 1 or your list will only end up “nearly” sorted!

public List sort(List list) {

assert list != null : “list cannot be null”;

for (int i = 0; i < _increments.length; i++) { int increment = _increments[i];

hSort(list, increment);

}

return list;

}

Next, create the hSort() implementation, being careful to ignore increments that are too large for the data you are trying to sort. There’s not much point 50-sorting a list with only ten items, as there will be nothing to compare each item to. You require your increment to be less than half the size of your list.

149

Chapter 7

The rest of the method simply delegates to the sortSubList() method once for each position, starting at 0 as you did in the sample list:

private void hSort(List list, int increment) { if (list.size() < (increment * 2)) {

return;

}

for (int i=0; i< increment; ++i) { sortSublist(list, i, increment);

}

}

Finally, you create the method that sorts every H-th item relative to each other. This is an in-place version of insertion sort, with the added twist that it considers only every H-th item. If you were to replace every occurrence of + increment and – increment in the following code with + 1 and – 1, you’d have a basic insertion sort. Refer to Chapter 6 for a detailed explanation of insertion sort.

private void sortSublist(List list, int startIndex, int increment) {

for (int i = startIndex + increment; i < list.size(); i += increment) { Object value = list.get(i);

int j;

for (j = i; j > startIndex; j -= increment) { Object previousValue = list.get(j - increment);

if (_comparator.compare(value, previousValue) >= 0) {

break;

}

list.set(j, previousValue);

}

list.set(j, value);

}

}

How It Works

The shellsort code works by successively sorting sublists of items that are evenly spaced inside the larger list of items. These lists start out with few items in them, with large gaps between the items. The sublists become progressively larger in size but fewer in number as the items are more closely spaced. The outermost loop in the main sort() method is concerned with H-sorting the sublists at progressively smaller increments, eventually H-sorting with H set to a value of 1, which means the list is completely sorted.

The hSort() method is concerned with ensuring that all of the sublists that are made up of items separated by the current increment are correctly sorted. It works by looping over the number of sublists indicated by the current increment and delegating the actual sorting of the sublist to the sortSublist() method. This method uses an insertion sort algorithm (explained in Chapter 6) to rearrange the items of the sublist so that they are sorted relative to each other.

150

Advanced Sorting

Understanding Quicksor t

Quicksort is the first sorting algorithm discussed that uses recursion. Although it can be recast in an iterative implementation, recursion is the natural state for quicksort. Quicksort works using a divide-and- conquer approach, recursively processing smaller and smaller parts of the list. At each level, the goal of the algorithm is three-fold:

To place one item in the final sorted position

To place all items smaller than the sorted item to the left of the sorted item

To place all items greater than the sorted item to the right of the sorted item

By maintaining these invariants in each pass, the list is divided into two parts (note that it is not necessarily divided into two halves) that can each be sorted independently of the other. This section uses the list of letters shown in Figure 7-11 as sample data.

Q U I C K S O R T I S G R E A T F U N

Figure 7-11: Sample list for quicksort.

The first step in quicksort is to choose the partitioning item. This is the item that ends up in its final sorted position after this pass, and partitions the list into sections, with smaller items to the left (arranged randomly) and larger items to its right (arranged randomly). There are many ways to choose the partitioning item, but this example uses a simple strategy of choosing the item that happens to be at the far right of the list. In Figure 7-12, this item is highlighted. You also initialize two indexes at the leftmost and rightmost of the remaining items, as shown in the figure.

Q U I C K S O R T I S G R E A T F U N

Figure 7-12: Starting position for the initial quicksort pass.

The algorithm proceeds by advancing the left and right indexes towards each other until they meet. As the left index proceeds, it stops when it finds an item that is larger than the partitioning item. As the right index proceeds, it stops when it encounters an item that is smaller than the partitioning item. The items are then swapped so that they are each in the appropriate part of the list. Remember that the idea is to have smaller items to the left and larger items to the right, although not necessarily in sorted order.

In the example shown in Figure 7-12, the left index is pointing to the letter Q. This is larger than the partitioning value (N), so it is out of place at the far left of the list. The right index was initially pointing at U, which is larger than N, so that’s okay. If it moves one position to the left, it is pointing at the letter F, which is smaller than N. It is therefore out of place at the far right of the list. This situation is displayed in Figure 7-13.

151

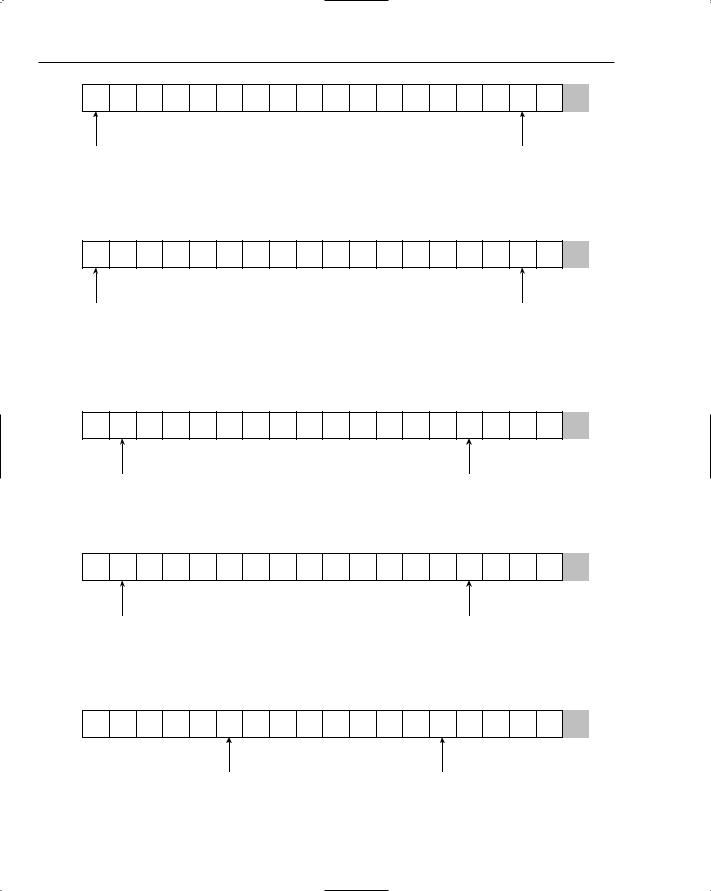
Chapter 7

Q U I C K S O R T I S G R E A T F U N

Figure 7-13: The first two out-of-place items have been found.

To get these two out-of-place items closer to their final sorted position, you swap them as shown in Figure 7-14.

F U I C K S O R T I S G R E A T Q U N

Figure 7-14: The first two out-of-place items are swapped.

The left index now continues moving to the right until it encounters an item that is larger than the partitioning item. One is found immediately in the second position (U). The right index then proceeds moving to the left and finds an A out of place, as shown in Figure 7-15.

F U I C K S O R T I S G R E A T Q U N

Figure 7-15: Two more out-of-place items are found.

Once again, the items are swapped, as shown in Figure 7-16.

F A I C K S O R T I S G R E U T Q U N

Figure 7-16: The second pair of out-of-place items are swapped.

The same procedure continues as the left and right indexes move toward each other. The next pair of out-of-place items are S and E, as shown in Figure 7-17.

F A I C K S O R T I S G R E U T Q U N

Figure 7-17: Two more out-of-place items are found.

152

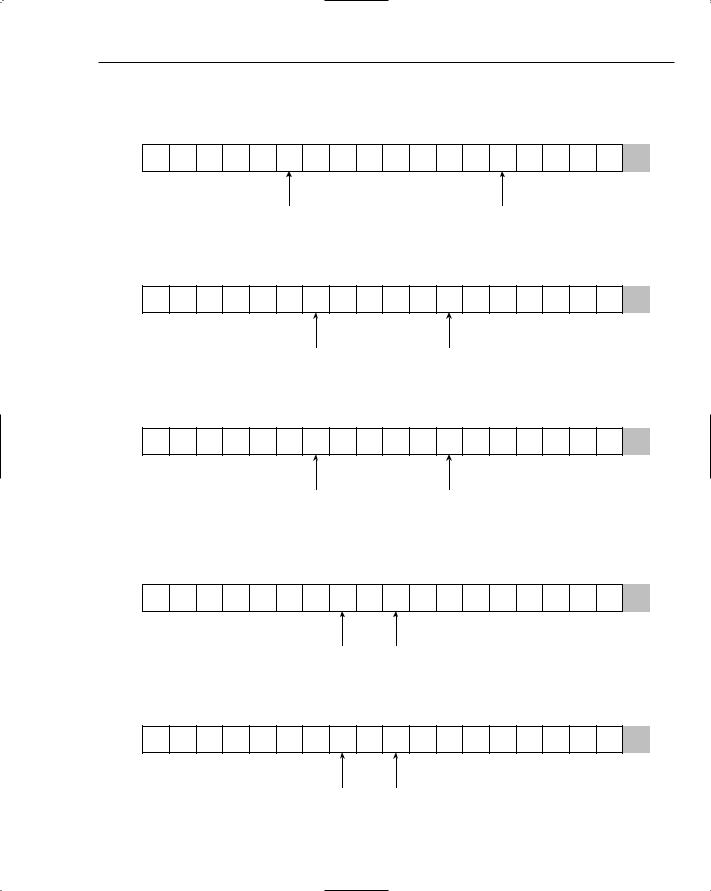
Advanced Sorting

You swap these items, leaving the list in the state shown in Figure 7-18. At this stage, every item to the left of the left index is less than the partitioning item, and every item to the right of the right index is larger than the partitioning item. The items between the left and right indexes still need to be handled.

F A I C K E O R T I S G R S U T Q U N

Figure 7-18: The letters E and S are swapped.

You continue with the same procedure. The next out-of-place items are shown in Figure 7-19.

F A I C K E O R T I S G R S U T Q U N

Figure 7-19: The letters O and G are out of place.

You swap them into the position shown in Figure 7-20.

F A I C K E G R T I S O R S U T Q U N

Figure 7-20: The letters O and G are swapped.

You are almost done for the first quicksort pass. Figure 7-21 demonstrates that one pair of out-of-place items remain.

F A I C K E G R T I S O R S U T Q U N

Figure 7-21: The letters R and I are out of place.

After you swap them, the list is in the state shown in Figure 7-22.

F A I C K E G I T R S O R S U T Q U N

Figure 7-22: The letters R and I are swapped.

153