Гришин Зачет по аналитической геометрии.1 семестр 2009
.pdf
Зачет по аналитической геометрии. 1 семестр Вариант 8
1.ABCDEF – правильный шестиугольник. Рассматриваются векторы 
, 
и 
. Представить вектор 
в виде линейной комбинации векторов 
и 
.
2.ADCDEF – правильный шестиугольник (см. задачу 1) со стороной 1. Найти: 1) длину вектора 
; 2) угол между
вектором 
и вектором 
; 3) модуль векторного произведения векторов 
и 
.
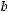3. Найти единичный вектор , составляющий равные углы с векторами |
, |
|
и |
|
|||
. |
|
|
|
4.Дан параллелограмм ABCD с вершинам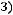и 
, 
, 
и 
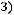. Написать уравнение прямой,
относительно которой все его вершины равноудалены. |
|
|
5. Написать уравнение плоскости, содержащей ось |
и равноудаленной от двух точек |
и |
.
6.Найти координаты точки, симметричной точке 
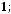
относительно плоскости 
.
7.Исследовать кривую второго порядка и построить ее график:
.
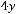
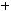
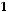
8. Для заданных матриц 
и 
решить матричное уравнение: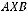 
,
11
Зачет по аналитической геометрии. 1 семестр Вариант 9
1.ABCDEF – правильный шестиугольник. Рассматриваются векторы 
, 
и 
, где М – точка пересечения продолжений сторон CD и FE. Представить вектор 
в виде линейной комбинации векторов 
и 
.
2.ADCDEF – правильный шестиугольник (см. задачу 1) со стороной 2. Найти: 1) длину вектора 
; 2) угол между
вектором 
и вектором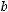 
; 3) площадь треугольника ACM.
3. Даны три вектора |
|
|
|
и |
|
Найти объем параллелепипеда, |
|
|
|
построенного на векторах 
, 
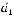
и 
.
4.Дан параллелограмм ABCD с вершинами 
, 
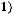и 
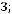
. Написать уравнение прямой высоты, проведенной из вершины A на сторону ВС.
5.Даны четыре точки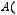 
, 
, 
и 
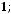
Написать уравнение плоскости, параллельной прямой 
и равноудаленной от всех четырех точек.
6.Найти координаты точки, симметричной точке 
относительно прямой 
.
7.Исследовать кривую второго порядка и построить ее график:
.
8. Для заданных матриц 
и 
решить матричное уравнение: 
,
12
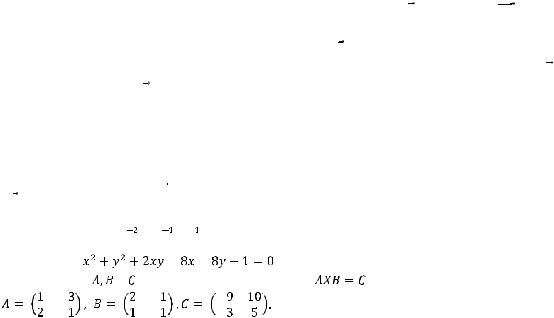
Зачет по аналитической геометрии. 1 семестр Вариант 10
1.ABCDEF – правильный шестиугольник. Рассматриваются векторы 
, 
и 
, где М – точка пересечения продолжений сторон BC и DE, а N – точка пересечения продолжений сторон AF и BC. Представить вектор 
в виде линейной комбинации векторов 
и 
.
2.ADCDEF – правильный шестиугольник (см. задачу 1) со стороной 1. Найти: 1) длину вектора 
; 2) угол между вектором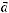 
и вектором 
; 3) площадь четырехугольника ABMF.
3.Даны три вектора 
, 
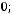
и 
. При каком значении 
вектор 
будет перпендикулярен вектору 
?
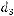4.Дан треугольник ABC с вершинами 
, 
и 
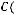
. Написать уравнение прямой биссектрисы угла
при вершине А.
5. Даны три точки 
, 
и 
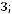
. Написать уравнение плоскости, параллельной АС и вектору 
и равноудаленной от точек A, B и C.
6.Найти проекцию прямой 
на плоскость 
.
7.Исследовать кривую второго порядка и построить ее график:
8. Для заданных матриц |
|
|
|
|
|
|
. |
|
||||
|
|
|
||||||||||
и решить матричное уравнение: |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
Зачет по аналитической геометрии. 1 семестр Вариант 11
1.ABCD – прямоугольник. Рассматриваются векторы 
, 
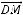и 
, где М – середина стороны ВС. Представить вектор 
в виде линейной комбинации векторов 
и 
.
2.ADCD – прямоугольник (см. задачу 1), длины сторон которого равны: 
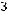
. Найти: 1) длину
вектора 
; 2) угол между вектором 
и вектором 
; 3) площадь параллелограмма, построенного на векторах 
и 
.
3.Даны три вектора 
, 
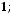
и 
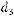
. Найти вектор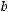 
, перпендикулярный векторам
и |
, такой, что площадь параллелограмма, построенного на векторах и , равна |
|
. |
4.Дан треугольник ABC с вершинами 
, 
и 
. Написать уравнение прямой медианы
|
треугольника, проведенной из вершины B, и найти угол между этой медианой и биссектрисой угла А. |
|
|
||||||||||||||||||
5. |
Написать уравнение плоскости, все точки которой равноудалены от двух плоскостей |
|
|
|
и |
||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Найти уравнение прямой, симметричной прямой |
|
|
|
|
|
|
|
|
|
|
|
относительно плоскости |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
.
7.Исследовать кривую второго порядка и построить ее график: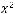 
.
8.Для заданных матриц 
и 
решить матричное уравнение: 
,
14
Зачет по аналитической геометрии. 1 семестр Вариант 12
1. ABCD – прямоугольник. Рассматриваются векторы |
|
, |
|
и |
|
, где М – середина стороны |
BC, N – середина стороны CD. Представить вектор 
в виде линейной комбинации векторов 
и 
.
2.ADCD – прямоугольник (см. задачу 1), длины сторон которого равны: 
. Найти: 1) длину
вектора ; |
2) угол между вектором |
|
и вектором ; 3) площадь четырехугольника AMCN. |
||||||
3. Даны три |
вектора |
|
|
, |
|
|
и |
|
. Найти вектор , коллинеарный вектору |
|
|
|
|||||||
, такой, что объем параллелепипеда, построенного на векторах 
, 
и 
, равен 9.
4.Дан треугольник ABC с вершинами 
, 
и 
. Точки 
и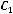 
симметричны вершинам A и C относительно прямых BC и АВ. Написать уравнение прямой 
.
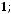
5.Найти угол, который составляет плоскость, проходящая через точки 
, 
и 
, с координатной плоскостью ZOY.
6.Найти расстояние между двумя скрещивающимися прямым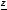и 
и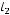 
.
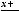
7.Исследовать кривую второго порядка и построить ее график:
.
8. Для заданных матриц 
и 
решить матричное уравнение: 
,
15
Зачет по аналитической геометрии. 1 семестр Вариант 13
1. ABCD – прямоугольник. Рассматриваются векторы |
|
, |
|
и |
|
, где М – середина стороны |
ВС. Представить вектор 
в виде линейной комбинации векторов 
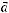и 
.
2.ADCD – прямоугольник (см. задачу 1), длины сторон которого равны: 
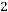. Найти: 1) длину вектора 
; 2) угол между вектором 
и вектором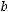 
; 3) модуль векторного произведения 
и 
.
3.Даны три вектора 
, 
и 
. Найти вектор 
, компланарный векторам 
и 
, и такой, что площадь параллелограмма, построенного на векторах 
и 
, равна 
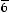, если известно, что проекция вектора 
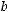на ось OZ равна 1.
4.Дан треугольник ABC с вершинами 
, 
и 
. Написать уравнение прямой, симметричной прямой АВ относительно прямой АС.
5. |
Написать уравнение плоскости, проходящей через точку |
|
параллельно вектору |
|
|
|
|
|
|
и |
||||||||
|
|
|||||||||||||||||
|
составляющую угол 450 с плоскостью |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. |
Написать уравнение плоскости, проходящей через точку |
|
перпендикулярно прямой |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7.Исследовать кривую второго порядка и построить ее график: 
.
8. Для заданных матриц 
и 
решить матричное уравнение: 
,
16
Зачет по аналитической геометрии. 1 семестр Вариант 14
1. ABCD – прямоугольник. Рассматриваются векторы |
|
, |
|
и |
|
, где М, N и P |
– середины |
сторон АВ, BC и CD соответственно. Представить вектор |
в виде линейной комбинации векторов |
и . |
|||||
2.ABCD – прямоугольник (см. задачу 1), длины сторон которого равны: 
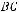
. Найти: 1) длину вектора 
; 2) угол между вектором 
и вектором 
; 3) площадь параллелограмма, построенного на векторах 
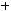
и 
.
3.Даны три вектора 
, 
и 
. Найти вектор 
длины 3, компланарный векторам 
и 
и перпендикулярный вектору 
.
4.Дан треугольник ABC с вершинами 
, 
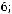
и 
. Написать уравнение прямой, симметричной
прямой медианы, проведенной из вершины A, относительно прямой ВС.
5. Найти расстояние между двумя параллельными плоскостями 
и 
.
6. Написать уравнение прямой перпендикуляра, опущенного из точки |
|
на прямую |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||
7.Исследовать кривую второго порядка и построить ее график:
.
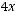
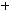
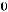8. Для заданных матриц 
и 
решить матричное уравнение: 
,
17
Зачет по аналитической геометрии. 1 семестр Вариант 15
1.ABCD – прямоугольник. Рассматриваются векторы 
, 
и 
, где точки М и N расположены на стороне BC так, что 
. Представить вектор 
в виде линейной комбинации векторов 
и
.
2.ADCD – прямоугольник (см. задачу 1), длины сторон которого равны: 
. Найти: 1) длину вектора 
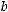; 2) угол между вектором 
и вектором 
; 3) площадь параллелограмма, построенного на векторах 
и 
.
3.Даны три вектора 
, 
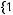
и 
. Найти вектор 
, перпендикулярный оси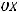 
,
компланарный векторам 
и 
и имеющий проекцию на вектор 
равную 
.
4.Дан треугольник ABC с вершинами 
, 
и 
. Написать уравнение прямой средней линии треугольника, параллельной стороне АС, и найти расстояние между этой прямой и стороной АС.
5. |
Две параллельные плоскости |
|
|
|
|
и |
|
пересекают плоскость |
||||||
|
|
|
|
|
||||||||||
|
|
|
по двум параллельным прямым. Найти расстояние между этими прямыми. |
|||||||||||
|
|
|
||||||||||||
6. |
Написать уравнение прямой, |
проходящей через точку |
|
|
|
и параллельной двум плоскостям |
||||||||
|
|
|||||||||||||
|
|
|
и |
|
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
7.Исследовать кривую второго порядка и построить ее график: 
.
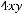
8.Для заданных матриц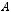 
и 
решить матричное уравнение: 
,
18
Зачет по аналитической геометрии. 1 семестр Вариант 16
1. |
В |
прямоугольном параллелепипеде |
|
рассматриваются векторы |
|
, |
|
|
|
|
|
|
и |
||||||||
|
|
|
|
, где E – середина ребра |
. Представить вектор |
в виде линейной комбинации векторов |
, |
и . |
|||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
В |
прямоугольном |
параллелепипеде |
(см. задачу 1) |
длины |
ребер равны: |
|
|
|
|
|
|
|
|
|
. |
Найти: |
||||
|
1) |
длину вектора |
; 2) угол между вектором |
и вектором ; 3) объем пирамиды, построенной на |
|||||||||||||||||
векторах 
, 
и 
.
3.Даны три вектора 
, 
и 
. Найти вектор 
, если известно, что его
проекции на векторы |
, и |
равны |
|
, |
|
и |
|
|
|
соответственно. |
|
|
4.Дан четырехугольник ABCD с вершинами 
, 
, 
и 
. Через точки B и D
|
проведены прямые, перпендикулярные диагонали АС. Написать уравнения этих прямых и найти расстояние |
|||||||||||||||
|
между ними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Написать уравнение плоскости, перпендикулярной двум плоскостям |
|
|
|
|
|
|
|
и |
|
|
|||||
|
|
|
||||||||||||||
|
и проходящей через точку |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. |
Написать уравнение плоскости, проходящей через точку |
|
и прямую |
|
|
|
|
. |
|
|
||||||
|
|
|
||||||||||||||
7.Исследовать кривую второго порядка и построить ее график:
.
8.Для заданных матриц 
и 
решить матричное уравнение: 
,
19
Зачет по аналитической геометрии. 1 семестр Вариант 17
1. |
В прямоугольном параллелепипеде |
|
рассматриваются векторы |
|
|
, |
|
|
|
|
|
|
|
|
|
и |
||||||||||||||||||||||||||||||
|
|
|
, где E – середина ребра |
. Представить вектор |
в виде линейной комбинации векторов , |
и . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
В прямоугольном параллелепипеде (см. задачу 1) длины ребер равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Найти: |
||||||||||||||||||||||||
|
1) длину вектора ; 2) угол между вектором |
|
|
|
и вектором |
; |
|
3) объем пирамиды, построенной на |
||||||||||||||||||||||||||||||||||||||
|
векторах , |
и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Даны три |
вектора: |
|
|
, |
|
|
|
|
|
|
и |
|
|
|
. |
Найти вектор |
, |
компланарный с |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
векторами |
и , имеющий проекции на векторы |
|
и |
, равные |
|
|
и |
|
|
|
соответственно. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
4. |
Дан четырехугольник ABCD с |
вершинами |
|
|
|
|
|
, |
|
|
, |
|
|
|
|
|
и |
|
|
|
|
|
|
. Точки |
|
и |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
симметричны точкам B и C относительно диагоналей АС и BD . Написать уравнение прямой |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
5. |
Написать уравнение плоскости, перпендикулярной |
|
плоскости |
|
|
|
|
|
, |
|
параллельной вектору |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
и проходящей через точку |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6.Найти координаты точки пересечения прямой 
и плоскости 
.
7.Исследовать кривую второго порядка и построить ее график:
.
8. Для заданных матриц 
и 
решить матричное уравнение: 
,
20