Рассмотренные выше моменты являются общими (интегральными) характеристиками распределения случайной величины. Вторая группа параметров характеризует отдельные значения функции распределения. К ним относятся квантили. Квантилем хβ распределения случайной величины Х с функцией распределения F(x) называется решение уравнения F(xβ) = β, т. е. такое значение случайной величины, что Р(Х ≤ xβ) = β. Наиболее важное значение имеет квантиль х1/2, называе-

мый медианой распределения (рис. 6).

Рис. 6. Медиана распределения.

Ордината медианы пополам рассекает площадь между кривой плотности вероятности и осью абсцисс. Если распределение симметрично, то х1/2 = mx

2.2.Нормальное и стандартное распределения случайной величины. Функция Лапласа. Задача об абсолютном отклонении.

Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения имеет вид

где mx и σ2x — математическое ожидание и дисперсия случайной величины Х.

22

Функция распределения равна

Нормальное распределение наиболее часто встречается на практике и теоретически наиболее полно разработано. Множество событий происходит случайно вследствие воздействия на них большого числа независимых (или слабо зависимых) возмущений, и у таких явлений закон распределения близок к нормальному. Установлено, что нормальное распределение содержит минимум информации о случайной величине

по сравнению с любыми распределениями с той же дисперсией. Следо-

вательно, замена некоторого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений, что ши-

роко используется на практике.

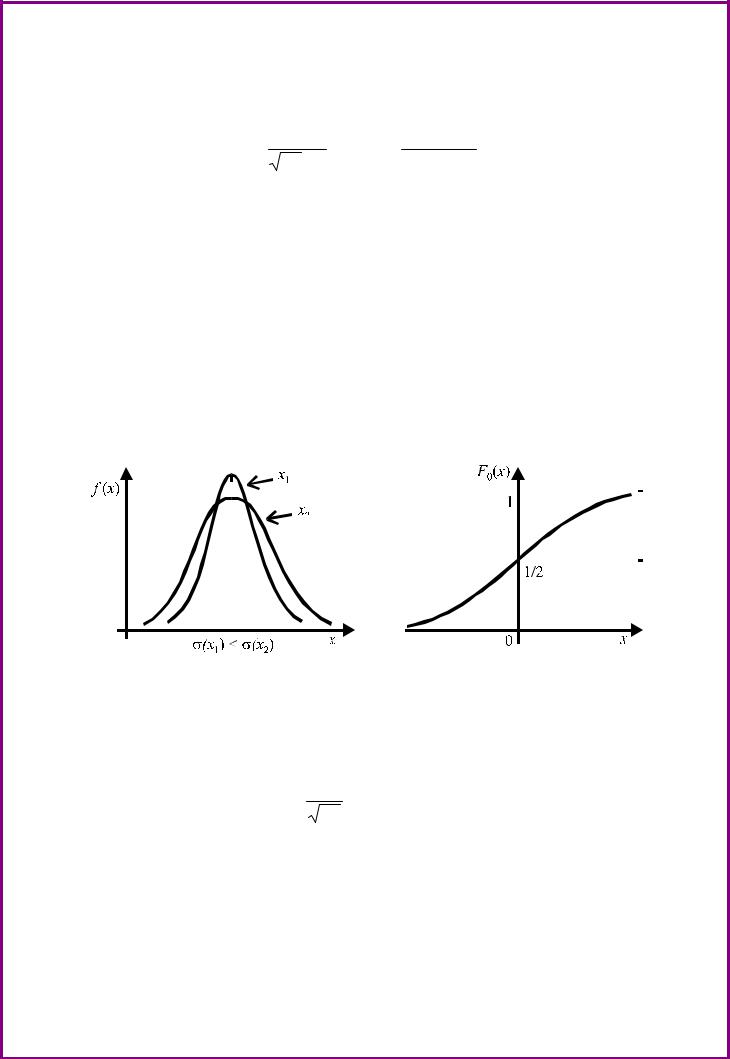
График плотности нормального распределения называется нор-

мальной кривой, или кривой Гаусса (рис. 7).

Нормальное распределение нормированной случайной величины называется стандартным. Его функция распределения имеет вид

−∞

а график этой функции представлен на рис. 8.

Вероятность того, что значения нормированной случайной величины будут лежать в интервале от х01 до х02, равна

23

Значения функции Лапласа табулированы (приложение 1). Так как она является нечетной функцией, т. е. Ф(-х) = -Ф(х), то таблицы значений Ф(х) составлены лишь для х > 0.

Для нормированной случайной величины с учетом (2.27) и (2.28) имеем:

Во многих практических задачах х1 и х2 симметричны относительно математического ожидания, в частности в задаче об абсолютном от-

клонении. Абсолютным отклонением является величина

Требуется найти вероятность того, что абсолютное отклонение случайной величины не превзойдет некоторого заданного числа ε:

Тогда для нормально распределенной случайной величины с параметрами mx и σх справедливо

Обозначив ε/σх = k, из (2.35) получаем

24

Таким образом, отклонения больше, чем утроенный стандарт (утроенное стандартное отклонение), практически невозможны. На практике часто величины 2σх (или 3σх ) считают максимально допустимой ошибкой и отбрасывают результаты измерений, для которых величина отклонения превышает это значение, как содержащие грубые ошибки.

Нормальное распределение обладает также свойством линейности: если независимые случайные величины Х1 и Х2 имеют нормальные распределения, то для произвольных чисел α и β величина

Y = αX1 + βX2

также имеет нормальное распределение, причем из свойств математического ожидания и дисперсии следует, что

25