матан коллоквиум / 10.Основные теоремы дифференциального исчесления.Теорема Ферма,Лангранжа
..docxТеорема Ферма
Пусть
функция 
или 
в
т.
■
□ Пусть,
для определённости,
(рис.
10.1), тогда
при
и
Согласно
определению производной имеем
◙
Рис. 10.1
Геометрическое
истолкование теоремы вытекает из
геометрического смысла производной:
касательная к графику функции 
в
точке с абсциссой
параллельна
оси
.
10.1.2. Теорема Ролля
Пусть
функция
.
Тогда
■
□ Из
условия
следует
по свойству 10 непрерывных
на
функций,
что
.
Существует две возможности:
1) 
;
2) 
в
силу
.
Пусть
,
тогда согласно теореме Ферма
.
Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.
10.1.3. Теорема Лагранжа
Пусть
функция
.
Тогда
■
□ Введём
на
вспомогательную
функцию
,
для которой верны условия теоремы
Ролля:
или
.
Следовательно
.
Солгасно
т. Ролля
:
◙
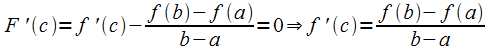Геометрическое
истолкование теоремы Лагранжа. Строим
график функции
(рис.
10.2), 
.
Угловой коэффициент касательной в т. 
.
Следовательно, на графике функции
.
Рис. 10.2
10.1.4. Теорема Коши
Пусть
функции 
.
Тогда
■
В
формуле
.
В противном случае согласно теореме
Ролля
.
□ Введём 
.
Подберём такое
,
чтобы
Тогда
.
По теореме Ролля 
.
Теорема
Коши является обобщением теоремы
Лагранжа, где 
.