
матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек
..docxЭкстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть
дана функция ![]() и
и ![]() —
внутренняя точка области определения
—
внутренняя точка области определения ![]() Тогда
Тогда
-
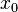 называется
точкой локального максимума функции
называется
точкой локального максимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
-
 называется
точкой локального минимума функции
называется
точкой локального минимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
Если
неравенства выше строгие, то ![]() называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.
-
 называется
точкой абсолютного (глобального)
максимума, если
называется
точкой абсолютного (глобального)
максимума, если
![]()
-
 называется
точкой абсолютного минимума, если
называется
точкой абсолютного минимума, если
![]()
Значение
функции ![]() называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Достаточные условия существования локальных экстремумов
-
Пусть функция
 непрерывна
в
непрерывна
в  и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные  .
Тогда при условии
.
Тогда при условии
![]()
![]() является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
![]()
то ![]() является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
Заметим,
что при этом функция не дифференцируема
в точке ![]()
-
Пусть функция
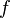 непрерывна
и дважды дифференцируема в точке
непрерывна
и дважды дифференцируема в точке  .
Тогда при условии
.
Тогда при условии
![]() и
и ![]()
![]() является
точкой локального максимума. А если
является
точкой локального максимума. А если
![]() и
и ![]()
то ![]() является
точкой локального минимума.
является
точкой локального минимума.
-
Пусть функция
 дифференцируема
дифференцируема 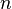 раз
в точке
раз
в точке  и
и  ,
а
,
а  .
.
Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального максимума. Если
-
точка локального максимума. Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального минимума. Если
-
точка локального минимума. Если ![]() нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
Максимум и минимум функции.
Приведем
точные определения точек
экстремума.
Определение. Точка
x0 называется
точкой минимума функции f, если для всех
x из некоторой окрестности x0 выполняется
неравенство f(x) ≥ f(x0.
Это
наглядно показано на рисунке 1:
 рисунок
1
Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0.
Это
наглядно показано на рисунке 2:
рисунок
1
Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0.
Это
наглядно показано на рисунке 2:
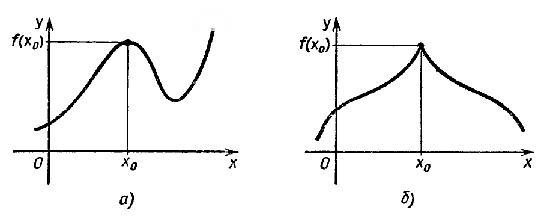 рисунок
2
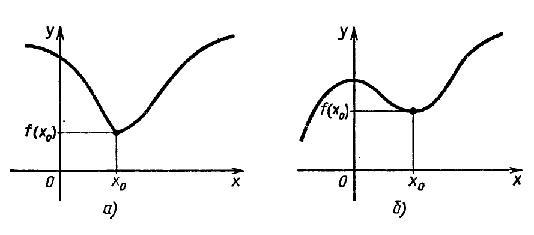
По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно).
Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
рисунок
2
По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно).
В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно).
Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже:
 Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для
точек минимума и максимума функции есть
общее определение - точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название - экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
Слева
направо: a - точка максимума; a - точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума.
Для
точек минимума и максимума функции есть
общее определение - точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название - экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума - xmin.
Критической
точкой дифференцируемой
функции ![]() ,
где
,
где ![]() —
область в
—
область в ![]() ,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
,
называется точка, в которой все её частные
производные обращаются
в ноль. Это условие эквивалентно обращению
в ноль дифференциала функции
в данной точке, а также равносильно
горизонтальности касательной гиперплоскости
к графику
функции.
Это условие является необходимым (но
не достаточным) для того, чтобы внутренняя
точка области
могла быть точкой локального
минимума или
максимума функции.
