матан коллоквиум / 3.Дифиренцируемость функци связь непрерывности и деффиренцируемости.Понятие дифференциала и его геометрический смысл

Дифференци́руемая фу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.

Функция дифференцируема в точке тогда и только тогда, когда у неё существует конечная производная. Более того

Дифференциал функции (соответственно производная) определяется единственным образом.

Функция, дифференцируемая в какой-либо точке, непрерывна в ней же, то есть

Обратное, вообще говоря, неверно.

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращение х. Функция получит приращение у. Найдем .

.

Следовательно, у=f(x) непрерывна в точке х₀.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Пример. у=|х| , х₀=0.

 

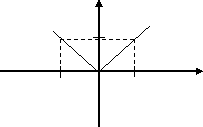            Y

 

            0                            X

 

 

 

 

 

 

 

х>0,             ;

х<0,             .

В точке х₀=0 функция непрерывна, но производной не существует.

Понятие дифференциала

Пусть функция y = f(x) дифференцируема при некотором значении переменной x . Следовательно, в точке xсуществует конечная производная

Тогда по определению предела функции разность

                            (1)

является бесконечно малой величиной при . Выразив из равенства (1) приращение функции, получим

                    (2)

(величина  не зависит от , т. е. остаётся постоянной при ).

Если , то в правой части равенства (2) первое слагаемое линейно относительно . Поэтому при

оно является бесконечно малой того же порядка малости, что и . Второе слагаемое - бесконечно малая более высокого порядка малости, чем первое, так как их отношение  стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

                (3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

или

Следовательно,

                   (4)

или

             (5)

Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (5) это видно из записи, в формуле (4) – нет.

Дифференциал функции можно записать в другой форме:

                      (6) или

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении xна величину .