матан коллоквиум / 2.Геометрический смысл производной.косательная и её уравнения,понятие нормалей

Геометрический смысл производной

.

Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е.

где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.

Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид

Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линииу = f(x) в точке Мо(хо, уо) запишется так:

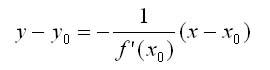
Касательной к графику функции y=f(x) в точке  называют прямую, проходящую через точку , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к .

Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции  в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции , касательная прямая показана синей линией, точка касания изображена красной точкой.

Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

Хорошо видно, что вблизи точки касания график функции  практически сливается с касательной прямой y=x+1.

А сейчас перейдем к более значимому определению касательной.

Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А.

Рисунок ниже иллюстрирует этот процесс.

Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей  (показан красной прерывистой дугой) будет стремиться к углу наклона касательной  (изображен красной сплошной дугой).

Определение.

Таким образом, касательная к графику функции y=f(x) в точке А – это предельное положение секущей AB при .

Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.

Нормаль — это прямая, ортогональная (перпендикулярная) касательному пространству (касательной прямой к кривой, касательной плоскости к поверхности и т. д.).

Уравнение нормали к графику функции f(x) в точке x0, при условии, что f'(x0) ≠ 0 имеет вид: