Михеев Исполнителные устройства автоматических 2008

Статические характеристики ЭММ с массивным якорем при питании от источника тока, определяемые выражением

(QT )cp = 12 (Iw)δ2 ∂∂Gxδ ,

будут иметь тот же вид, что и у ЭММ постоянного тока, поскольку сигналом управления в обоих случаях является намагничивающая

сила Fу=Iу wу.

Если же обмотка управления подключена к источнику напряжения u =U m cosωt , то условия работы ЭММ существенно

изменятся. В статическом режиме работы электрическую цепь ЭММ с ненасыщенным магнитопроводом можно приближенно

Из последнего выражения следует, что для ЭММ с X L >>R, при питании от генератора напряжения, величине управляющего сигнала пропорциональна не намагничивающая сила катушки Fy ,

а поток Ф ≈ ωUwy . При ненасыщенном магниитопроводе

значение потока ЭММ переменного тока не зависит от его магнитного сопротивления, т.е. от положения якоря. Мгновенное значение силы тяги qТ ЭММ с притягивающимся плоским якорем

41

(см. рис. 2.1, а) находим по выражению (2.1) с учетом того, что

определяется только сигналом управления и не зависит от положения якоря. На рис. 2. 9 приведены статические характеристики ЭММ с магнитопроводом, обладающим идеальной кривой намагничивания, для этого режима работы, построенные по выражению (2.8).

а) б)

Рис. 2. 9

Статические характеристики реальных ЭММ переменного тока этого типа с учетом некоторого увеличения потока при δ→0 показаны на рис. 2.10, а, б. Приведенные выше уравнения справедливы, естественно, для ЭММ с ненасыщенными цепями.

42

а) б)

Рис. 2.10

Существенными недостатками ЭММ переменного тока с массивным якорем являются, во-первых, меньшая сила тяги, чем в ЭММ постоянного тока с такими же размерами магнитопровода, и, во-вторых, пульсация силы тяги, приводящая к быстрому разрушению шарнирных соединений в ЭММ и нагрузке, и к сильному шуму. Если первый недостаток является органическим следствием синусоидальной формы переменного тока и избавиться от него можно только переходя к переменному току прямоугольной формы, то второй недостаток можно существенно ослабить довольно простыми средствами, рассмотренными ниже.

2.2.2. Конструктивные особенности ЭММ переменного тока

Для уменьшения пульсации силы тяги, которая вызывает вредную вибрацию подвижных деталей, используют ЭММ с несколькими магнитными потоками, сдвинутыми по фазе относительно друг друга. Использование многофазной системы напряжений питания, например трехфазной, для создания многофазной системы магнитных потоков оправдано только для мощных ЭММ. Маломощные ЭММ желательно подключать к однофазной сети. В этом случае целесообразно использовать ЭММ с двухфазной магнитной системой при однофазном питании. На рис. 2.11 приведена схема ЭММ, в котором фазовый

сдвиг потока относительно Ф1 осуществляется путем сдвига тока

43

I2 по фазе относительно I1 с помощью конденсатора, включенного последовательно с обмоткой w2 .

На якорь электромагнита будет действовать сумма двух сил от потоков Ф1 и Ф2 :

где φ– угол сдвига фаз между Ф1 и Ф2 , равный сдвигу фаз между

I1 и I2 .

Преобразуя последнее выражение, получаем:

Если не выполняется хотя бы одно из этих условий, имеет место пульсация силы тяги, амплитуда которой из выражения (2.9) равна:

∆Qср = Q1ср +Q2ср + 2Q1срQ2ср cos 2ϕ.

44

В реальных электромагнитах в диапазоне полного перемещения якоря условие φ = π/2 выполнить практически невозможно, так как при перемещении якоря изменяется индуктивность обмоток, что приводит к изменению фазового

сдвига между токами I1 и I2 (при постоянной величине емкости

С). Обычно выбирают емкость конденсатора С из условия получения угла φ, близкого к π/2, при том положении якоря, которое он занимает большую часть времени работы.

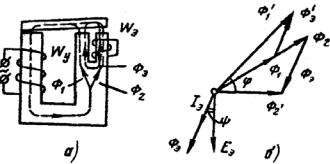
Конструктивно и технологически более простым и экономичным способом получения сдвига фаз между двумя потоками является использование короткозамкнутых обмоток (электромагнитных экранов), которые охватывают часть магнитопровода,. На рис. 2.12, а приведена схема ЭММ с таким экраном, а на рис. 2.12, б – векторная диаграмма для магнитной цепи. Поток в части магнитной цепи, охваченной витками

короткозамкнутой катушки экрана wэ , определяется НС катушки управления wу и НС катушки экрана.

Рис. 2.12

Используя метод суперпозиции, этот поток представим в виде: Ф2′ = Ф2 + Фэ, где Ф2 – поток, определяемый сигналом управления; Фэ– поток, определяемый током Iэ в экране.

Поток Ф2′ индуцирует в катушке wэ ЭДС Eэ, отстающую от него на π/2. Ток в экране Iэ отстает от Еэ на небольшой угол,

45

зависящий от величины потока рассеяния катушки wэ. Поток же Фэ совпадает по фазе с Iэ. Вычитая Фэ из Ф2′, найдем Ф2 , который

совпадает с Ф1 . Суммируя Ф1 с частью потока экрана Фэ′(с обратным экраном), проходящего по участку сердечника, не охваченного экраном, получаем результирующий поток Ф1′, проходящий по этому участку магнитопровода. Потоки Ф1′ и Ф2′ с

фазовым сдвигом φ и создают составляющие силы тяги qТ1 и qТ2. Из векторной диаграммы следует, что угол φ в данной схеме невозможно сделать равным π/2, так как φ = π/2 может быть только при ψ=0 и при Фэ → ∞, что потребует Iэ → ∞. Последнее условие соответствует бесконечно большой мощности, выделяемой в катушке экрана. Необходимо также учитывать, что при установке экрана снижается регулирующий поток, и, следовательно, несколько уменьшается сила тяги ЭММ.

2.3. Реверсивные электромагнитные механизмы

2.3.1. Принцип действия реверсивных ЭММ

Реверсивными ЭММ постоянного тока (поляризованными) называют ЭММ, у которых направление перемещения якоря или плунжера зависит от полярности сигнала управления. Реверсивными ЭММ переменного тока называют ЭММ, у которых направление перемещения якоря определяется фазой напряжения управления. Из реверсивных ЭММ в автоматических устройствах относительно широко используются ЭММ постоянного тока, поэтому только они и будут рассмотрены ниже.

Работа реверсивного ЭММ постоянного тока основана на сравнении направления управляющего потока Фу, создаваемый обмоткой управления, с направлением вспомогательного так называемого поляризующего потока Фп, создаваемого постоянным магнитом или вспомогательной обмоткой. Все конструктивные разновидности реверсивных ЭММ по конфигурации магнитной цепи можно разбить на дифференциальные и мостовые. На рис. 2.13, а приведен поляризованный электромагнит с дифференциальной магнитной

46

цепью, а на рис. 2.13, б – ее схема замещения в пренебрежении потоками утечки. На рис. 2.13, в дана схема поляризованного электромагнита с мостовой магнитной цепью, а на рис. 2.13, г – ее схема замещения. На рис. 2.13, б, г Fу – НС обмотки управления, Fп – НС постоянного магнита, создающего поляризующий поток. Якорь электромагнита размещен в зазоре, образованном двумя полюсами сердечника. Таким образом, в поляризованном ЭММ имеются два рабочих зазора, через которые проходят и поляризующий, и управляющий потоки, но в одном из зазоров они направлены согласно, а в другом – встречно. Поэтому результирующая сила, действующая на якорь, по величине и направлению зависит от величины и направления потока управления.

Рис. 2.13

47

2.3.2. Статические характеристики реверсивных ЭММ

Рассмотрим статические характеристики на примере реверсивного ЭММ с мостовой магнитной цепью (рис. 2.13, в). Пренебрегая потоками утечки и магнитным сопротивлением стали, схему замещения для этой цепи можно представить в виде схемы рис. 2.13, г. Считая приближенно рабочий зазор (между якорем и сердечником) ограниченным плоскопараллельными поверхностями, и пренебрегая потоками выпучивания, выражения для сопротивлений рабочих воздушных зазоров слева и справа от якоря можно записать в виде:

Чтобы рабочий зазор не шунтировался сердечником 2 (рис. 2.13, в), между ним и сердечником 1 вводят дополнительные воздушные зазоры, сопротивление которых на схеме обозначается

Результирующие потоки в зазорах δ′ и δ′′ равны:

Из этого выражения можно получить уравнение статической характеристики рассматриваемого ЭММ при принятых допущениях в виде:

−δ2 ≤ х ≤ +δ2 .

На рис. 2.14, а, б приведены семейства регулировочных и внешних характеристик, построенных по уравнению (2.10).

Рис. 2.14

49

У реальных реверсивных ЭММ из-за конечных значений магнитных сопротивлений R0 и стали, а также наличия потоков

утечки и выпучивания статические характеристики нелинейны (рис. 2.15, а, б).

Рис. 2.15

В зависимости от вида нагрузочной характеристики реверсивные ЭММ могут быть преобразователями и дискретного, и непрерывного действия. Большинство реверсивных ЭММ используется в так называемых поляризованных реле и дистанционных переключателях, в которых нагрузкой якоря является упругая сила пружин. На рис. 2.16, а, б приведено построение внешних и регулировочных характеристик реверсивного ЭММ, нагруженного пружиной с большим

коэффициентом упругости ( KП = Qxc >| ∂∂QxT |x=0 ) .

Рис. 2.16

50