
Демидов Основы программирования в примерах на языке ПАСЦАЛ 2010
.pdfvar e: integer; begin
c := a + b; d := c;
e := c; writeln('Подпрограмма:');
writeln('c = ', c, ' d = ', d, ' e = ', e); end;
begin
a := 3; b := 5; x(a, b, c, d);
writeln('Главная программа:');
writeln('c = ', c, ' d = ', d, ' e = ', e); end.
Результаты работы программы:
Подпрограмма:
c = 8 d = 8 e = 8
Главная программа: c = 0 d = 8 e = 0
Значение переменной «с» в главной программе не изменилось, поскольку переменная передавалась по значению, а значение переменной е не изменилось, потому что в подпрограмме была описана локальная переменная с тем же именем.
Здесь следует отметить, что глобальные переменные автоматически инициализируются 0, однако это поведение может отличаться в зависимости от компилятора языка. Поэтому не стоит рассчитывать на автоматическую инициализацию, а выполнять её самостоятельно.
91
Глава 9. Рекурсивные процедуры и функции
Рекурсивные подпрограммы, условие выхода из рекурсии
Как было рассмотрено в предыдущих главах, процедура (функция) представляет собой обособленный поименованный участок программы, который может вызываться из основной программы, а также из другой процедуры (функции). Однако ничто не мешает процедуре (функции) вызывать саму себя. Подпрограмма, в которой содержится обращение к самой себе, называется рекурсивной, при этом имеет место прямая рекурсия.
Ранее была построена функция Calculate, которая из-за использования её имени в качестве локальной переменной случайно вызывала саму себя. При этом она никогда бы не завершила своей работы из-за бесконечной рекурсии, так как у нее не было возможности не выполнять рекурсивный вызов.
Рассмотрим пример другой рекурсивной функции:
function r(n: integer): integer; begin
if n <= 1 then r := 1 else r := n * r(n - 1);
end;
Данная программа вычисляет значение факториала, при этом используется рекуррентное соотношение n! = n*(n–1)!, где 1! = 1. Здесь вычисления завершатся, поскольку после серии рекурсивных вызовов при n = 1 выполнится основная ветвь условного оператора. Такое условие называют условием выхода из рекурсии, а ветвь, не содержащая рекурсивных вызовов, именуется терминальной.
Если одна подпрограмма вызывает другую, а та в свою очередь первую, то имеет место косвенная рекурсия:
procedure FА(…); begin
...
FB(…);
...
end;
procedure FВ(…);
92
begin
...
FA(…);
...
end;
Однако по правилам языка Pascal нельзя использовать объект раньше, чем он был описан. Таким образом, определение подпрограммы FA некорректно, поскольку имеет ссылку на неопределенный объект FB(). В этих случаях необходимо объявить (но не определять!) процедуру FB до процедуры FA. В языке Паскаль это выполняется с помощью директивы forward после заголовка подпрограммы. Например:
procedure FВ(a: integer); forward;
procedure FА(a: integer); begin
...
FB(…);
...
end;
procedure FВ(a: integer); begin
...
FA(…);
...
end;
Косвенная рекурсия часто используется при обработке динамических структур данных.
Правила построения рекурсивных подпрограмм:
1)рекурсивная подпрограмма должна иметь хотя бы одну терминальную ветвь, переход на которую должен осуществляться в зависимости от некоторого условия (условия выхода);
2)проверка условия выхода должна предшествовать рекурсивным вызовам, в противном случае условие никогда не будет проверено.
93
Итерация и рекурсия. Сравнение подходов
Рассмотрим пример рекурсивной функции, вычисляющей значение n-го члена ряда Фибоначчи:
function fib(n: integer): integer; begin
if n <= 2 then fib := 1
else fib := fib(n-1) + fib(n-2); end;
Функция fib содержит два рекурсивных вызова, а в общем случае рекурсивных вызовов в теле подпрограммы может быть сколько угодно. Как видно из программного кода, эта рекурсивная функция, как и функция вычисления факториала, практически копирует рекуррентные соотношения, определяющие n-й член ряда. Таким образом, рекурсия оказывается более компактным способом реализации рекуррентных соотношений, нежели итерация. Существуют задачи, в частности обработка динамических структур данных, для которых рекурсия – наиболее естественный способ решения.
Но насколько эффективен этот способ? Итеративный алгоритм вычисления чисел Фибоначчи имел линейную временную сложность и константную емкостную сложность. Чтобы оценить временную сложность рекурсивного алгоритма необходимо рассчитать общее число операций, выполняемых в результате всех рекурсивных вызовов. Вызов подпрограммы будем считать одной операцией. Для n=1 или n=2 выполняются одна проверка условия выхода и возврат значения (две операции), а для остальных случаев после проверки условия выполняются два вычитания, два рекурсивных вызова, сложение и присваивание (семь операций). К этому числу ещё необходимо добавить число операций, выполняемых в результате двух рекурсивных вызовов. Тогда:
для n = 3 имеем ∑(3) = 7 + ∑(2) + ∑(1) = 7+2+2 = 11 операций; для n = 4 имеем ∑(4) = 7 + ∑(3) + ∑(2) = 7+11+2 = 20 операций; для n = 5 имеем ∑(5) = 7 + ∑(4) + ∑(3) = 7+20+10 = 37 операции;
…
Обобщая, получаем ∑(n) = 7 + ∑(n–1) + ∑(n–2), где ∑(2) = 2, ∑(1) = 2.
Итак, получено рекуррентное соотношение, напоминающее соотношение для n-го члена ряда Фибоначчи, что для выбранного
94
способа реализации вполне ожидаемо. Таким образом, сложность |
||||||||||||||
рекурсивного алгоритма пропорциональна fib(n). Для получения |
||||||||||||||
аналитического вида функций fib(n) и ∑(n) необходимо вспомнить |
||||||||||||||
удивительное свойство чисел Фибоначчи: |
|
|
|
|
||||||||||
fib(n) |
1 |
5 1,618... |
|
|
|
|
|
|||||||
fib(n 1) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Тогда для больших n |
|
|
|
|
|
|
|
|
|
|
||||
fib(n) 1,618 1,618n |
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, функция fib(n) оказывается прямо пропорцио- |
||||||||||||||
нальна 1,618n. То же самое справедливо и для ∑(n). Рассмотрим |
||||||||||||||
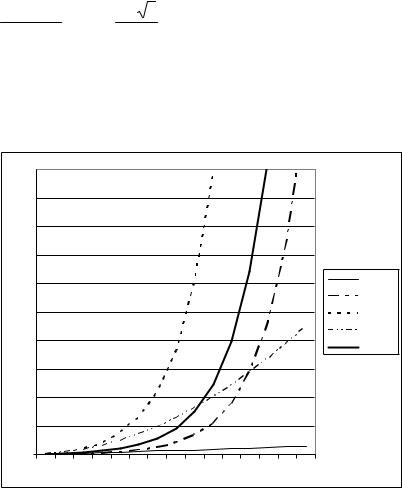
графики функций fib(n), ∑(n) и 1,618n, представленные на рис. 6: |
||||||||||||||
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
450 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
350 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
fib(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑(n) |
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n^2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,618^n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Рис. 6. График функции fib(n) в сравнении с другими
Видно, что графики fib(n) и sigma(n) повторяют форму графика 1,618n, а сами функции связаны соотношениями
fib(n) = 0,4475*1,618n; ∑(n) = 4,028*1,618n.
95

Таким образом, сложность рекурсивного алгоритма оценивается как O(1,618n). Можно заметить, что функция fib(n) возрастает быстрее n2 и в точке n = 12 перегоняет её. Столь низкая производительность рекурсивной функции fib(n) объясняется тем, что вычисления многократно повторяются. Визуально рекурсивные вызовы можно представить в виде дерева, где число повторных вычислений растёт при углублении рекурсии (рис. 7).
fib(n)
fib(n-1) |
|
fib(n-2) |
|
|
|
fib(n-2) |
|
fib(n-3) |
|
fib(n-3) |
|
fib(n-4) |
|
|
|
|
|
|
|
fib(n-3) fib(n-4)
Рис. 7. Дерево рекурсивных вызовов fib(n)
Интуитивно понятно, что с точки зрения расхода памяти рекурсивный алгоритм также не на высоте. Чтобы понять, что происходит при рекурсивных вызовах необходимо обратиться к реализации самого механизма вызова подпрограмм в операторных языках программирования.
Реализация рекурсии в операторных языках. Стек вызовов подпрограмм
При вызове подпрограммы системное окружение программы выполняет ряд действий:
96
1)запоминается место возврата управления в вызывающей программе (подпрограмме). Поскольку все инструкции программы хранятся в оперативной памяти, то каждая исполняемая команда имеет свой адрес. Таким образом, запоминается адрес команды, следующей за вызовом подпрограммы. Кроме того, могут запоминаться состояния системных переменных, в частности регистров процессора, для гарантии их сохранности после работы подпрограммы;
2)вычисляются значения фактических параметров, выполняется контроль типов;
3)для всех локальных переменных подпрограммы и параметров, передаваемых по значению, выделяется память. Кроме того, могут быть выделены дополнительные системные ресурсы. Вычисленные значения параметров передаются подпрограмме;
4)управление передается первому оператору подпрограм-
мы.
После завершения работы подпрограммы выделенные ресурсы возвращаются системе, восстанавливаются состояния переменных, управление передается обратно. Таким образом, использование подпрограмм связано с определенными накладными расходами.
Для хранения адресов возврата и состояний окружения (значений параметров и переменных) используется стек. Стеком называется упорядоченный набор некоторого переменного числа объектов, работающий по правилу: «Последним пришел, первым вышел» (от англ. LIFO – Last In, First Out). Схему работы стека можно проиллюстрировать на следующем примере: представим, что машина заехала в узкий тупик, а за ней еще несколько машин. Выезжать они будут в обратном порядке, и последней выедет первая машина.
Такая схема работы позволяет организовать вложенные и рекурсивные вызовы подпрограмм: при вызове подпрограмм в стек добавляется информация, а после завершения работы она извлекается в обратном порядке.
Рассмотрим работу стека и порядок вычислений fib(n) для n = 4:
fib(4) в стек проверка n<=2
выделение памяти для промежуточных переменных @1,@2,@3
fib(3) в стек
97
проверка n<=2
выделение памяти для промежуточных переменных @4,@5,@6
fib(2) в стек проверка n<=2
возврат 1 @41 (извлечение из стека)
fib(1) в стек проверка n<=2
возврат 1 @51 из стека
@6 = @4 + @5 = 2
возврат @6 @12 из стека
fib(2) в стек проверка n<=2
возврат 1 @21 из стека
@3 = @1+@2 = 3
возврат @3
3 из стека
Видно, что расчёта числа Фибоначчи требуется сначала рекурсивно погрузиться на максимальную глубину, а лишь затем вычислить сумму:
fib(4)
fib(4-1) + fib(4-2) fib(3) + fib(2)
(fib(3-1) + fib(3-2)) + fib(2) (fib(2) + fib(1)) + fib(2)
(1 + fib(1)) + fib(2) (1 + 1) + fib(2)
2 + fib(2)
2 + 1
3
При этом память тратится не только на обеспечение рекурсивных вызовов в стеке, а еще и на хранение многочисленных вспомогательных локальных переменных.
Для рекурсивных подпрограмм накладные расходы многократно увеличиваются с ростом числа рекурсивных вызовов. При большой глубине рекурсии существует реальная опасность переполнения стека. Если же в рекурсивной процедуре по каким-либо причинам условие выхода всегда ложно или терминальная ветвь отсутствует, то переполнение стека неизбежно.
98
Вообще, отладка рекурсивных процедур гораздо сложней, так как в один и тот же момент времени могут выполняться несколько экземпляров рекурсивной функции. Все они имеют одно и то же имя, поэтому для локализации места возникновения ошибки требуется анализировать значения передаваемых параметров.
Хвостовая рекурсия и аккумуляторы, оптимизация рекурсивных программ
Глядя на дерево рекурсивных вызовов для функции fib(n), возникает желание избежать повторных вычислений. Рассмотрим следующий вариант реализации функции:
function fib(n: integer): integer;
function f(n, prev, pprev: integer): integer; begin
if n <= 2 then f := prev
else f := f(n-1, prev+pprev, prev); end;
begin
f(n, 1,1); end;
Дерево рекурсивных вызовов для fib(4) выглядит так:
fib(4) f(4, 1, 1)
f(4-1, 1+1, 1) f(3, 2, 1) f(3-1, 2+1, 2) f(2, 3, 2)
3
В отличие от первого варианта дерево не разрастается в ширину, память стека расходуется только на обеспечение рекурсивных вызовов, вычисления проводятся в постоянном объеме памяти и не дублируются. Так происходит потому, что вспомогательная функция в качестве параметров рекурсивного вызова передаёт уже вычисленную очередную пару чисел Фибоначчи, причём рекурсивный вызов выполняется последним действием. Рекурсия такого вида называется хвостовой.
Сложность вычислений fib(n) при хвостовой рекурсии линейна, а сам алгоритм может быть легко преобразован в итеративный с помощью циклов.
99
Правила построения рекурсивных подпрограмм с аккумулятором:
1)вводится вспомогательная функция с дополнительным параметром-аккумулятором, в котором будет накапливаться результат вычислений. В общем случае аккумуляторов может быть несколько;
2)главная функция вызывает вспомогательную функцию с начальными значениями аккумуляторов;
3)при выполнении условия выхода из рекурсии вспомогательная функция возвращает значение аккумулятора;
4)рекурсивный вызов вспомогательной функции выполняется с таким значением аккумулятора, которое возвращалось бы главной функцией.
Следует отметить, что далеко не для всех рекурсивных подпрограмм можно построить вариант с хвостовой рекурсией. Это процесс творческий.
Задание для самостоятельного выполнения: написать функцию вычисления факториала f(n)=n*f(n-1) с помощью хвостовой рекурсии.
Возможный вариант решения:
function fact(n: integer): integer; function f(n, acc: integer): integer; begin
if n <= 1 then f := acc else f := f(n-1, n*acc);
end; begin
f(n,1); end;
Проверка работы хвостовой рекурсии для 4!: fact(4)
f(4, 1) f(4-1, 4*1) f(3, 4) f(3-1, 3*4) f(2, 12) f(2-1, 2*12) f(1, 24)
24
100
