Дегтяренко Введение в физику неупорядоченных конденсированных 2011

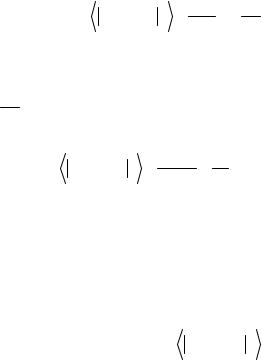
P.O.=Размерность и порядок=

Как известноI= одномерная решетка будет термически J не устойчиваK= В самом делеI= принимая во внимание довольно общие= условияI=которым удовлетворяет радиус действия межатомных силI= можно показатьI=что в одноJ=или двухмерных системах спонтанный= кристаллический порядок существовать не можетK==

Воспользуемся моделью гармонических колебаний решетки= и произведем обычные Фурье преобразования к фононным переJ меннымK= Тогда кроме формулы для корреляционной функции= = можно получить еще следующее соотношение:=

kq

Нас интересует поведение суммы в правой части этого соотJ ношения при больших значениях= oK= Знаменатель можно заменить=

на= hw и положить=E ws = sq I==где=s==–== скорость звукаFK=Интересуясь=====

kq

d-мерной решеткойI=получим:=

При=d=Z=N=этот интеграл пропорционален=oX=при=d=Z=O=он ведет себя= асимптотически как= lnoK= В обоих случаях флуктуации расстояния= между атомами в удаленных друг от друга узлах неограниченно= возрастают по мере увеличения этого расстоянияK= С другой стороJ ныI=при=d=Z=P=интеграл сходится к малой величинеI=не зависящей от= oI= так что предполагаемый порядок в решетке оказывается Jста бильнымK=

Очень сходный с этим результат легко получить для спиноJ

вой корреляционной функции= pl - pl+o O I= где=o==–== расстояние=

между удаленными узлами в упорядоченной ферромагнитной цеJ почкеK= Таким образомI= в одноJ= или двухмерной системе в отсутJ ствие факторовI=изменяющих спектр магнонов=Eконечного магнитJ

TN=

=

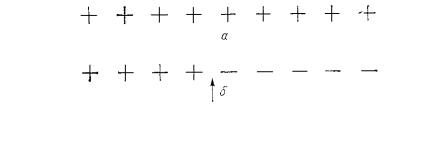
ного поля или магнитной анизотропииFI=спонтанный ферромагнитJ ный или антиферромагнитный порядок возникнуть не можетK=

В одномерной модели Изинга состояние спонтанного упоряJ дочения термодинамически неустойчиво=EрисKPKOFK=

=

=

=

=

РисK=PKOK= Дальний порядок в линейной цепочке= EаF= разрушаJ ется в результате одного единственного разрыва=EбF=

=

P.P.=Неупорядоченные линейные цепочки=

=

Однако рассмотрение моделей топологического беспорядка=

oi = l × a I==============================================EPKPF=

где= l = = –== целое числоK= Если величины= oi = – =случайныеI =то имеем= дело с одномерной жидкостью или одномерным стекломK=

Относительно расположения атомов в такой системе можно= выдвигать различные статистические гипотезыK=В простейшем слуJ чае величины= oi =–=независимые переменныеI=с постоянной вероятJ ностью распределенные по всей длине цепочкиK= Это одномерный= газK= Для характеристики его нужен лишь один статистический паJ раметр= –= плотность упаковки или обратное ей среднее расстояние= между частицами:=

a = i k K====================================EPK4F=

TO=

=

Предел выражения= EPK4F= при неограниченном возрастании= длины=i и числа атомов=k есть некоторая постояннаяK=

Поскольку абсолютная координата атома в цепочке не играет= существенной ролиI= лучше задать статистические характеристики= относительных координат атомовK= В модели одномерного газа поJ следовательные межатомные расстояния=

xi = oi+N - oi ===================================EPKRF=

распределены независимо и подчиняются распределению Пуассона==

m (x )dx = N ×e-xa × dx K========================EPKSF= a

Распределение Пуассона не подходит для конденсированных= системI= поскольку не учитывается конечный размер атомов= = –===

принцип плотной упаковкиK=Этой модели можно придать известное= правдоподобиеI= допустивI= что атомы непроницаемы и не могут= сблизиться на расстояниеI=меньшее некоторого минимального диаJ метра= aX= вместе с тем любой свободный зазорI= превышающий неJ которую длину=dI=будет занят другим атомомK=В этом и заключаетJ ся физическое обоснование модели БорландаI= согласно которой= межатомное расстояние должно лежать в некоторых фиксированJ ных пределах=

a £ xi £ d K===============================EPKTF=

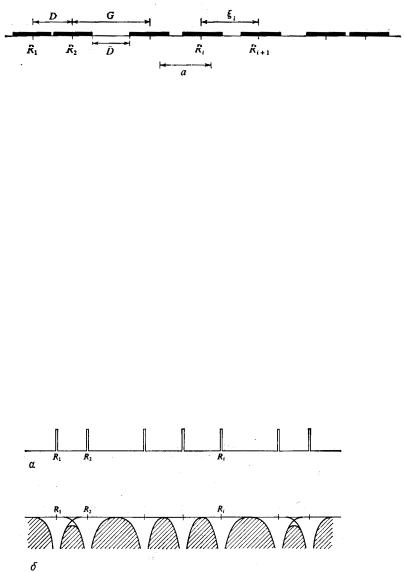
Согласно вычислениям по методу Монте-КарлоI=отрезки равJ ной длины могут быть случайно и без перекрытия распределены= вдоль некоторой линииI= пока их концентрация не превышает= MITR= концентрации в соответствующей регулярной плотно упакованной= структуреK= Другими словамиI= в рамках данной модели жидкости= разумен выбор=ac=Z=NLOd=»=MITR=аK=Фактически результат=MIT4TS=был= получен еще в=N9S4=гK=в так называемой=«задаче о стоянке автомоJ билей»K= Сходный результат получается и с помощью= «оборванноJ го»=распределения Пуассона для величин зазоров=EрисK=PKPFK=

TP=

=

=

РисKPKPK=Модель Борланда=

=

В некоторых случаях удобно рассматривать одномерную= гауссову жидкостьI= в которой каждая величина= xi подчиняется=

нормальному распределению с дисперсией= sO =и=средним значениJ

a

ем= аI= хотя на самом деле такой физической системыI= видимоI= не= существуетK=

P.P.N.=Модель Кронига=–=Пенни для неупорядоченной цепочки=

Задав расположение атомовI=нужно определить другие сущеJ ственные параметры моделиK= НапримерI= для изучения динамики= решетки одномерного стекла постулируемI= что межатомные силы= должны изменяться в зависимости от расстояния между соседними= атомамиK= ДалееI= учет изменений интегралов перекрытияI= содержаJ щих волновые функции электроновI= локализованных на соседних= атомахI=приводит к модели сильно связанных электронов в неупоJ рядоченных системахK==

=

РисK=PK4K=Модель беспорядка Кронига=– Пенни=EаFI=обобщение= на суперпозицию потенциалов случайно расположенных атомов=EбF=

T4=

=

=

В теории движения электронов в жидких металлах часто исходят= из неупорядоченной модели Кронига=–=ПенниI=в которой потенциJ альная энергия электрона в поле отдельного атома описывается= дельта-функцией=EрисKPK4F:=

s ErF = ådEr - oi F K=

i

P.4. Приводимый и неприводимый= топологический беспорядок=

=

Одномерная система не может быть топологически неупоряJ доченнойK= Почти во всех случаях можно построить регулярную= структуру с беспорядком замещенияI= математически эквивалентJ ную модели=«одномерной»=жидкостиK=

РисKPKRK= Неупорядоченная линейная цепочка= EаFI= однозначное= упорядочение путем пересчета= EбFI= эквивалентная упорядоченная= решетка со средней постоянной решетки=EвFI==цепочка теперь тоJ пологически упорядоченаI= однако смещения атомов не упорядочеJ

ны=EгF=

=

Относительные смещенияI= межатомное расстояние явно игJ рают роль случайных переменных замещения = вi-м узле эквиваJ лентной упорядоченной системыI=т.еK=можно расположить в возрасJ

TR=

=

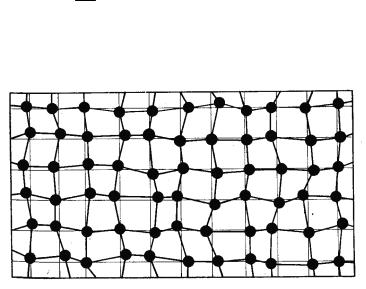
тающем порядке и с запретом на перескок атома через другой = (рисKPKRFK= В одномерном случае можно всегда существовавший= беспорядок= {xi } переместить на силовые константы= {hi }=Eмодуль= упругостиFK=

ji&&xi = - ¶F = -{hi }× o(i - oi+N )+ {hi-N}× (oi-N - oi K= ) ¶xi

Приводимый беспорядок может существовать= = в= OJмерных= (рисKPKSF=и в=PJмерных случаяхK=

=

РисK=PKSK=«Горячее твердое тело»=нельзя назвать топологиJ чески неупорядоченным=

=

P.R.=Физическая реализация одномерных систем=

Для создания магнитной цепочки необходимо найти материJ алI= в котором магнитные ионы взаимодействуют друг с другом= вдоль цепочекI= почти изолированных одна от другой большими= немагнитными ионамиI= радикалами или молекулярными группиJ ровкамиK= Такие материалы были найденыK= НапримерI= в бензоате= меди= EСuEСSНRСООFOJPНOОF= –= моноклинная решетка= –= большие= плоские бензоатные группы упакованы такI= чтоI= с одной стороныI=

TS=

=

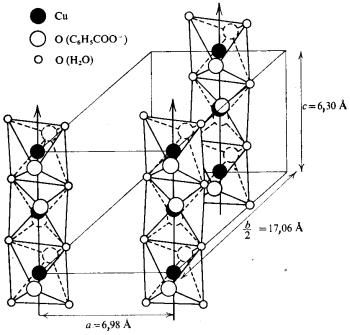
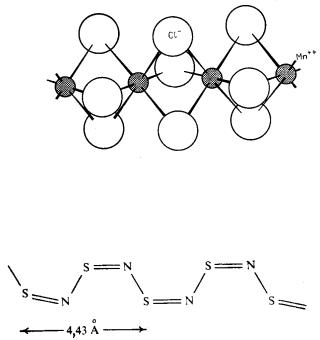
магнитные ионы СuHH могут сблизиться по оси=с на расстояниеI=где= обменное взаимодействие уже существенноK= А с другой стороныI=в= направлениях осей=а и=b цепочки удерживаются достаточно далеко= друг от друга= EрисK= PKTFK= Этот материал считается простым одноJ мерным антиферромагнетикомI= описываемым моделью ГейзенберJ га=

немI= по всей видимостиI= обменное взаимодействие между ионами= СuHH в цепочкахI=вытянутых вдоль оси=сI=осуществляется через свяJ

зи Сu=–=Сl=–=СuK==

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

РисKPKTK= Магнитные цепочкиI= возникающие в бензоате меJ диK= Остальная часть цепочки заполнена ионами бензоата и молеJ кулами воды=

TT=

=

=

Первым примером электронной одномерной системы могла бы= служить длинная полимерная цепьK= Однако в таких соединениях= связи почти всегда полностью насыщеныI=в результате чего поведеJ ние электронов в них определяется в основном корреляционными= эффектамиK= С равным правом здесь можно считатьI= что электроны= либо заполняют локализованные= EсвязывающиеF= орбиталиI= либо= делокализованные состоянияI=описываемые функциями БлохаK=

=

=

=

=

=

=

РисK= PK8K= Часть структуры ТММСI= содержащая магнитJ ную цепочку==

=

=

=

=

=

=

РисKPK9K= В полинитриде серы цепочкиI= соединенные ненасыJ щенными связямиI= вытянуты вдоль кристаллографического= направления=

=

T8=

=

проводимостьK= Она обусловлена переносом электронов вдоль проJ тяженных цепочекI= составленных из химически насыщенных свяJ зейI=т.еK=здесь имеет место нечто близкое к одномерному металлуK=

=

P.S.=Дислокационный==беспорядок=

Случай неприводимого топологического беспорядка в криJ сталле лучше всего описывается на языке теории дислокацийK= В= идеальном кристалле каждому атому соответствует однозначно= определенный набор координатK= Это просто целые числаI= кратные= векторам трансляции решеткиI= показывающиеI= как достичь данноJ го атомаI=исходя из некоторого фиксированного узлаI=принятого за= начало отсчетаK= Точное число шагов вдоль каждого основного= направления не зависит от пути перехода I=иследовательноI= предJ ставляет собой топологический инвариант решетки= Eпри этом шаJ гам вперед и назад отвечают соответственно положительные и отJ рицательные числаFK=ОднакоI=если в кристалле есть дислокацияI=то= нумерация атомов оказывается уже неоднозначной:= число шаговI= совершаемых на пути между узлами= А и= ВI =зависит теперь от выJ бранного пути=EрисKPKNMFK=

=

=

=

=

=

РисK=PKNMK=Неэквивалентные пути в решетке с дислокациейI=======

A=®=m=®=B=º=A=®=n=®=B=¹==A=®=o=®=B=¹=A=®=p=®=B=

=

T9=

=

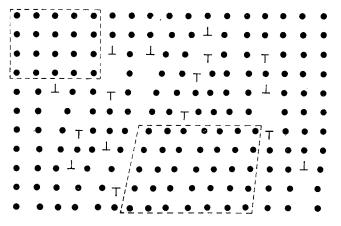
Всякий разI=когда траектория обходит линию дислокацииI=это= число меняется на единицуK=Таким образомI=кристалл с дислокациJ ями топологически не эквивалентен идеальной решетке=EрисKPKNNFK=

=

=

РисK=PKNNK=Дислокационный беспорядок в решетке с локальJ ным кристаллическим порядком=

=

P.T.=Поликристаллический беспорядок=

Другим примером топологического беспорядка может быть= поликристаллK= В этом случае удобно рассматривать каждыйJ от дельный кристаллитK= Каждый из них= –= почти идеальный образец= конечных размеровI=причем такихI=что для каждого из них размер= заметно больше средней длины свободного пробегаI=описывающей= микроскопические процессы релаксацииK= ДействительноI= в такой= системе атомы расположены беспорядочно лишь в тонких припоJ верхностных областях вблизи границ зеренK= Задачи о рассеянии= электроновI= фононовI= магнонов и тK= дK= на границах зерен можно= при этом рассматривать независимоK= ОднакоI= если макроскопичеJ ские характеристики кристалла не полностью изотропныI= то проJ хождение возмущений через такие границы определяется не столь=

8M=

=