Дегтяренко Введение в физику неупорядоченных конденсированных 2011

=

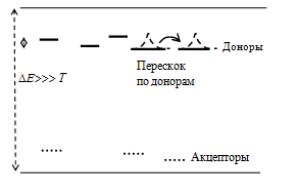РисK=8KOK==Прыжки электронов по примесямI=за счет малого= конечного перекрытия волновых функций примесных состояний=

=

В результате:=

-возникает переход части электронов с донорных примесей= на акцепторные и освобождение части мест на первыхX=

-появление положительно заряженных донорных примесей=

иотрицательно заряженных акцепторныхK=

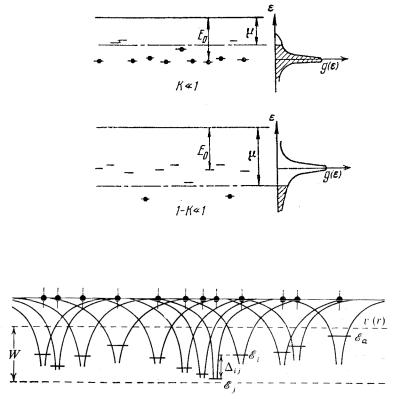
Второй факторI= в силу дальнодействия кулоновских полей и= хаотичного расположения в пространстве как техI= так и другихI= приводит к возникновению флуктуирующего в пространстве Jпо тенциала для донорных уровнейK= Создается разброс этих уровней= по энергииI= который значительно превышает малое расщепление= уровней соседних доноровI=связанное с перекрытием волновых= функций=EрисK8KPFK= На рисK=8KP=сплошная линия= –= зона проводимоJ стиI=штрих-пунктирная=–=уровень ФермиK=Короткие черточки изобJ ражают уровни доноровI=а темные кружки=–=занимающие их элекJ троныK= Справа изображена плотность состояний на донорных= уровняхK= Заполненные состояние заштрихованыK= Валентная зона и=

препятствует делокализации донорных электронов по примесям =и приводит к локализации состояния на отдельных донорахK=

N8N=

=

Вследствие разброса уровней по энергии нужен захват или=

концентрации примесейK=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

РисK= 8KPK= Энергетические схемы слабо и сильно компенсироJ ванных полупроводников в пренебрежении крупномасштабным= потенциальным рельефом=

РисK=8K4K=Перекрытие потенциалов примесных центров ведет= к разбросу энергий связанных состояний=

=

N8O=

=

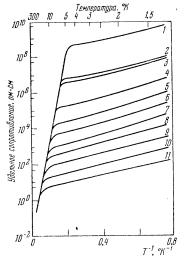
На рис=8KR=представлена зависимость удельного сопротивлеJ ния от обратной температуры для= de =p-типа со степенью компенJ сации====К=Z=MI4K=для различных значений концентраций примесейK= ХарактерноI= что при изменении= = концентрация увеличивается в= O= разаI=а сопротивление изменилось в=NMM=разK=

Концентрация= k уменьшаетсяI= следовательно расстояние= между примесями в среднем увеличиваетсяI= значит интеграл= перекрытия экспоненциально уменьшаетсяK= Тогда вероятность= перескока падаетI=а сопротивление растетK=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

РисK= 8KRK= Зависимость удельного сопротивления от темпеJ ратуры для=de=pJтипа со степенью компенсации====К=Z=MIQK==

Концентрация акцепторов=N=–=NN=равны=Eв см=JPFW=

N=–=TIR·NMNQX=O=–=NIQ·NMNRX=P=–=NIR·NMNRX=Q=–=OISS·NMNRX==

R=–=PIS·NMNRX=S=–=QIU·NMNRX=T=–=TIO·NMNRX=U=–=VIM·NMNRX== V=–=NIQ·NMNSX=NM=–=OIQ·NMNSX=NN=–=PIR·NMNS=

=

4K= В аморфных и органических полупроводниках= об электронных состоянияхI= по которым происходят прыжкиI= известно значительно меньшеI= чем в кристаллическихK= Эти= состояния связаны не с примесямиI=а с флуктуациями структуры и=

N8P=

=

стехиометрического составаK= Но и для аморфныхI= и для= кристаллических конденсированных тел при температурах=T=Y=N=h= возникает==зависимость вида==

возникает при выполнении условия=== 4p × k × ocP ; OKTR K=

P

Рассмотрим два уровня примесей= iI= àK= Разность энергий этих=

уровней= ei - e à = q =–=температуры ДебаяK=Перескок происходит с=

поглощением или испусканием одного фонона=EрисK8KSFK=

=

=

=

РисK=8KSK==Перескок носителя по примесным центрам=

=

N84=

=

числу переходов обратноI=i ↔=àK=

Поскольку электрического поля нет=Eb=Z=MFI= число переходов= должно быть одинаковым:==Ei=Þ=àF=Z=Eà=Þ=iFK=

N8R=

=

ДействительноI=поскольку существует токI=то его возникноJ вение может быть обусловлено только нарушением баланса переJ

N8S=

=

ность электрохимических потенциалов=–=напряжениеK=Тогда сопроJ тивление между= i-м и= à-м узлами= Eс точки зрения электротехничеJ ской задачиF=равно=

здесь температура=Т считается малым параметромK= Недостаток поJ лученного выражения заключается в его несимметричности отноJ сительно=iI=àK=Чтобы от этого избавитьсяI=в качестве меры разности= энергий берут симметричное по индексам выражение:=

eià = NO (ei - m + e à - m + ei - e à )K=

Итак:= oià = oiàM exp (xià )I=где= xià определено согласно формуле=E8KNFI=

выражениемI=симметричным по= eià K=

N8T=

=

В принципеI= локализованных примесных узлов многоI= они= разбросаны в пространствеK= У каждого узла своя реализация слуJ чайного потенциалаI=создаваемого заряженными примесями иI=слеJ довательноI=свой сдвиг по энергииK=У соседа может быть=«плохое»= окружениеI= которое сильно изменило энергетическое положение= его уровняI=а дальше в пространстве может оказаться примесьI=уроJ вень которой возмущен менееI= но==расстояние до него оказывается= большеK=

Получена сетка сопротивлений= oià I= соединяющая узлы приJ

месиK=Причем= oià меняется в чрезвычайно широком интервале знаJ

ченийK=

Неизвестное= Dm == может быть найдено из первого и второго=

законов Кирхгофа=Eравенство входящих=–=выходящих токов в кажJ дый узел и равенство суммы электрохимических потенциалов по= любому замкнутому контуруFK=

В слабо легированном полупроводнике среднее расстояние=

можно оценить как= kd-NP I= что соответствует расстоянию между=

примесями=»=S=–=NO=боровских радиусовK==

при этом сопротивление из-за экспоненциальной зависимости отJ личается в=NMNO=JNMO4 разK=Это объясняет экспериментальный график=

P ö÷ =EрисK8KTFK=

ø

Нужно произвести оценку в соответствии с теорией перколяJ цииK=Рассмотрим относительно большие температурыI=когда можно=

разорвем все сопротивления нашей системы и включим все= xià < x I=

N88=

=

постепенно увеличивая величину= xK= Две точки=EцентраF= считаются=

=

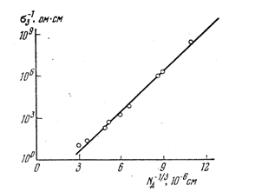
РисK8KTK=Проводимость= sP =pJгермания с примесью галлия как=

функция концентрации галлияK=Степень компенсации всех образцов=

К=Z=MIQ=

=

При определенной концентрации примесей будет возможно= протекание по системеK= Существует критический уровень заливки= xc I=при котором будет наблюдаться проводимость по всей системеI=

т.еK=образуется бесконечный кластерK=Можно провести аналогию с= повышением уровня воды до возникновения некоторого уровняI= когда все пруды=EсопротивлениеF=соединятся и создадут бесконечJ ный океан=EкластерFK=

=

8.O.=Концентрационная зависимость= прыжковой проводимости=

=

Для третьего интервала температур проводимость имеет вид==

N89=

=

т.еK= это термоактивированная проводимостьK= ПредэкпоненциальJ ный множитель= sP имеет сильную концентрационную зависиJ мостьK=Для данной температурной области характерно тоI=что=Т отJ носительно великаI=т.еK=всегда можно найти фонон для прыжка= eià K=

Orià K= a*

Данный= i-й узел связан со всеми другими узлами = àI= находяJ щимися внутри сферы некоторого радиуса=oI=описанной вокруг=i-го= узлаK= При некотором= o= Z= ocI как следует из = задачи о вложенных= сферах=EсмK= рисKTKNSFI= будет образовываться бесконечный кластерI= в котором каждый следующий узел лежит внутри сферыI= описанJ ной вокруг предыдущегоK=Тогда критическое значение параметра=x=

где= a =NI T4 K=

Способы проверки следующие:=

NK=ЭВМ и использование=NJго и=OJго законов КирхгофаI=точJ

ное решение для сопротивления= oià = oM exp(eià )I= где= eià =–=случайJ

ная величинаI==разбросанная в широком интервалеI= дает практичеJ ское совпадение результатовK=

OK= Экспериментальные результаты для= pJde= –= германиевый= полупроводник=р-типаK= Здесь задача является частично перколяциJ

N9M=

=