Х и не обязательно принадлежит этому подмножеству. Более того, мажоранта может и не существовать. В нашем примере на рис. 1.12 для подмножества Х мажоранта не существует.
Элемент xmij Y называется минорантой (нижней границей
или нижним конусом) Х тогда и только тогда, когда для любогоx X xmij ≤ x . Для примера на рис. 1.12 миноранты {a, b}.
Элемент xsup Y называется верхней гранью (точной верхней
гранью) Х тогда и только тогда, когда он является наименьшим среди мажорант. В нашем примере на рис. 1.12 для подмножества Х верхняя грань не существует.
Элемент xinf Y называется нижней гранью (точной верхней
гранью) Х тогда и только тогда, когда он является наибольшим среди минорант. В нашем примере на рис. 1.12 для подмножества Х нижняя грань {b}.
Теорема 1.5 (принцип двойственности). Отношение, обрат-
ное отношению упорядоченности, также является отношением упорядоченности.
Ранее мы использовали отношение ≤ . Обратное к нему отношение ≥ также упорядочено. Для него так же определяются экстремальные характеристики.
1.3.7. Отношение толерантности
Бинарное отношение T(M), заданное на множестве М, называ-
ется отношением толерантности (схожести) тогда и только тогда, когда оно рефлексивно и симметрично.
Например, задавая сходство между словами как различие в одну букву, можно строить различные переходы:
рука – рута – рота – рога – нога.
1.3.8. Операции над отношениями
Рассмотрим два отношения R1 и R2, заданных на множестве М
[1].
29
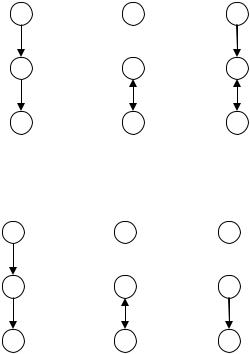
Объединением двух отношений R1 и R2 называется новое бинарное отношение R(M), элементы которого удовлетворяют условию:
R = R1 R2 ={(x, y) /(x, y) R1 или (x, y) R2 }.
Операция объединения обладает свойствами:
•коммутативности;
•ассоциативности;
•идемпотентности;
•для универсума и пустого бинарного отношения выполняются
R I = I , R = R.
На рис. 1.13 представлен результат объединения двух отношений.
a |
a |
a |
|
b |
b |
= b |
|
c |
c |
c |
Рис. 1.13 |
|
|
|
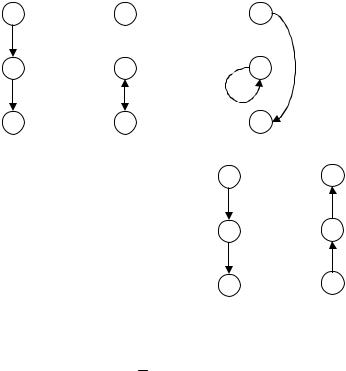
Пересечением двух отношений R1 и R2 называется новое бинарное отношение R(M), элементы которого удовлетворяют условию:
R = R1 ∩ R2 ={(x, y) /(x, y) R1 и (x, y) R2 }.
a |
a |
b ∩ |
b = |
c |
c |
Операция пересечения обладает свойствами:
•коммутативности;
•ассоциативности;
•идемпотентности;
a
b
c Рис. 1.14
30
для универсума и пустого бинарного отношения выполняются
R I R и R .
На рис. 1.14 представлен результат пересечения двух отношений.
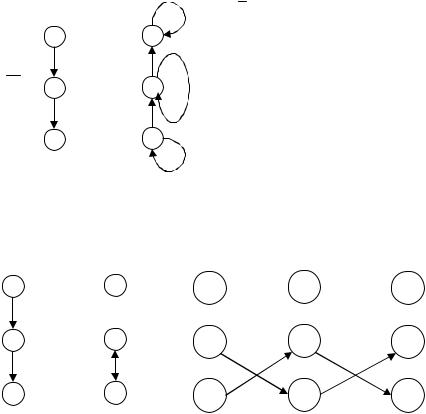
Композицией двух отношений R1 и R2 называется новое бинарное отношение R(M), элементы которого удовлетворяют условию:
R R1[R2 ] {(x, y)/ z :(x,z) R1 и (z, y) R2}.
Операция композиции обладает свойствами:ассоциативности;
для пустого бинарного отношения выполняются R[ ] =
и [R] = .
На рис. 1.15 представлен результат композиции двух отношений.
|
a |
|
a |
|
a |
|
b |
[ |
b |
] = |
b |
Рис. 1.15 |
c |
|
c |
|
c |
|
|
|
|
|
|
Обращением R–1 бинарного отно- |
a |
a |
|||
шения R(M) называется новое бинар- |
|||||
ное отношение R-1(M), удовлетво- |
|
|
|||
ряющее условию |
|
|
R-1( b ) = b |
||
R 1 {(x, y)/(y,x) R}. |
|||||
Операция обращения – унарная, |
|
|
|||
поэтому такие свойства, как коммута- |
c |
c |
|||
тивность, ассоциативность и т.д. для |
|||||
нее не определяются. На рис. 1.16 |
|
Рис. 1.16 |
|||
представлен результат |
обращения |
|
|
||
отношения.
Дополнением бинарного отношения R(M) до универсума назы-
вается новое бинарное отношение R(M):
31
a |
a |
R ( b ) = |
b |
c |
c |
Рис. 1.17 |
|
R(M) {(x, y)/(x, y) R}.
Операция дополнения – тоже унарная, поэтому для нее так же, как и для обращения, такие свойства, как коммутативность, ассоциативность и т.д., не определяются. На рис. 1.17 представлен результат дополнения отношения до универсума.
Декартовым произведением двух бинарных отношений называется новое бинарное отношение, элементы которого удовлетворяют условию (рис. 1.18)
|
R R1 |
R2 |
{((x,a),(y,b))/(x, y) R1 и |
(a,b) R2}. |
|
|
a |
|
a |
|
a,a |
b,a |
c,a |
b |
|
b |
= |
a,b |
b,b |
c,b |
c |
|
c |
|
a,c |
b,c |
c,c |
Рис. 1.18
Замыкание отношения относительно свойства. Рассмотрим два отношения R1 и R2 на множестве М, R2 обладает свойством S, S(R2). Отношение R1 называется замыканием R2 относительно свойства S тогда и только тогда, когда:
R1 обладает свойством S, S(R1);
R1 является надмножеством R2;
R1 – наименьшее.
Ядром отношения R на множестве M называется новое отношение R [R –1].
Отношение тождества U является ядром самого себя.
32