или
|
2 |
, 0 |
≤ μA (x) ≤ 0.5, |
|||
2A |
|
|||||
INT( A) = |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
, 0.5 ≤ μA (x) ≤1, |
||||
2A |
|
|||||
где A = ∫х/(1 − μA (x)) .
U
Эта операция отличается от концентрирования тем, что она увеличивает значение μA (x) , которое больше 0,5 и уменьшает те, ко-
торые меньше 0,5. Таким образом, контрастная интенсификация, по существу, уменьшает нечеткость А.
7.3.10. Операция «увеличение нечеткости»
Операция увеличения нечеткости, которая обозначается Ф(А),
противоположна операции контрастной интенсивности и выполняет процедуру превращения четкого множества в нечеткое или увеличения степени нечеткого множества.
Операция увеличения нечеткости определяется как
Φ( A) = 2 μA (x) (1 −μA (x)) (0.5 −μA (x)) + μA (x) .
Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.
7.4. Обобщенные нечеткие операторы
Жесткие, поточечно однозначные операторы, недостаточно полно отражают смысл многозначных лингвистических преобразований термов лингвистических переменных. Поэтому большой практический интерес представляет построение обобщенных нечетких операторов, т.е. параметризованных операторов пересечения, объединения, дополнения и др. Весьма общий и изящный подход к целенаправленному формированию нечетких операторов пересечения и объединения заключается в их определении в классе треугольных норм и конорм.
250
7.4.1. Треугольные нормы
Треугольной нормой Т (сокращенно t-нормой) называется двухместная действительная функция T :[0,1] ×[0,1] →[0,1] , удовлетво-
ряющая следующим условиям:
1)ограниченность: T (0,0) = 0 , T (μA ,1) =T (1,μA ) = μA ;
2)монотонность: μA ≤ μC ,μB ≤ μD T (μA ,μB ) ≤T (μC ,μD ) ;
3)коммутативность: T (μA , μB ) ≤T (μB , μA ) ;
4)ассоциативность: T (μA ,T (μB , μC )) =T (T (μA , μB ),μC ) .
Треугольная норма T является архимедовой, если она непрерывна и для любого нечеткого множества μA выполнено неравен-
ство Т(μA , μА ) ≤ μA . Она называется строгой, если функция T
строго возрастает по обоим аргументам. Примерами треугольных норм являются операторы, показанные в табл. 7.3.
|
Таблица 7.3 |
|
Треугольные нормы |
||
|
|
|
Определение функций T (x, y) = |
Имя функции |
|
|
|
|
0, если max(x, y) <1, |
Ограниченное произведение |
|
= |
||
min(x, y), если max(x, y) >1 |
|
|
= max(0, x + y −1) |
Усиленная сумма (пересечение |
|
по Лукасевичу) |
||
|
||
= x y / [1+(1− x) (1− у)] |
Произведение Эйнштейна |
|
= x y |
Алгебраическое произведение |
|
|
(вероятностное) |
|
= x y / [1−(1− x) (1− y)] |
Произведение Гамахера |
|
= min(x, y) |
Минимум (пересечение по Заде) |
|
|
|
|
7.4.2. Треугольные конормы
Треугольной конормой (сокращенно t-конормой) называется двухместная действительная функция :[0,1]×[0,1] →[0,1] , удовле-
творяющая следующим условиям:
1)ограниченность: (1,1) =1, (μA ,0) = (0,μA ) = μA ;
251
2)монотонность: μA ≥ μC ,μB ≥ μD (μA ,μB ) ≥ (μC ,μD ) ;
3)коммутативность: (μA , μB ) ≤ (μB , μA ) ;
4)ассоциативность: (μA , (μB , μC )) = ( (μA , μB ), μC ) .
Треугольная конорма является архимедовой, если она непрерывна и для любого нечеткого множества μA выполнено неравен-
ство (μA , μА ) ≥ μA . Она называется строгой, если функция
строго убывает по обоим аргументам. Примерами треугольных конорм являются операторы, показанные в табл. 7.4.
|
Таблица 7.4 |
|
Треугольные конормы |
||
|
|
|
Определение функций |
Имя функции |
|
(x, y) = |
||
|
||
|
|
|
= max(x, y) |
Максимум (объединение по Заде) |
|
=1 − (1 − x) (1 − y) / (1 − x y) |
Сумма Гамахера |
|
=1 − (1 − x) (1 − y) или = x + y – xy |
Алгебраическая сумма |
|
=1 − (1 − x) (1 − y) / (1 + x y) |
Сумма Эйнштейна |
|
= min(1, x + y) |
Усиленная разность (объединение |
|
по Лукасевичу, ограниченная |
||
|
сумма) |
|
|
|
|
1, если min(x, y) > 0, |
Ограниченная сумма |
|
= |
||
max(x, y), если min x(x, y) = 0 |
|
|
|
|
|
Рассмотрим следующие шесть пар t-норм и t-конорм (табл. 7.5).
|
Таблица 7.5 |
Пары t-норм и t-конорм |
|
|
|
t-норма |
t-конорма |
Усиленное произведение |
Усиленная сумма |
Ограниченная сумма |
Ограниченная разность |
Произведение Эйнштейна |
Сумма Эйнштейна |
Алгебраическое произведение |
Алгебраическая сумма |
Произведение |
Сумма Гамахера |
Минимум |
Максимум |
252
Для каждой пары справедливы уравнения:
T (x, y) =1− (1 − x,1 − y) ,(x, y) =1 −T (1 − x,1 − y) .
Для любых заданных значений х и у, таких, что х + у < 1, справедлива возрастающая последовательность: 0 ≤ усиленная сумма ≤ усиленное произведение ≤ произведение Эйнштейна ограниченная разность ≤ алгебраическое произведение ≤ произведение Гамахера
≤минимум ≤ максимум ≤ сумма Гамахера ≤ алгебраическая сумма
≤сумма Эйнштейна ≤ усиленная разность ≤ ограниченная сумма ≤ 1.
7.4.3. Декомпозиция нечетких множеств
Множеством уровня α (α-срезом) нечеткого множества А на-
зывается четкое подмножество универсального множества U, определяемое по формуле
Aα ={x | μA (x) ≥ α} ,
где α [0,1] .
По сути α – некоторый порог. Порог α = 0,5 называется точкой перехода.
Множество строгого уровня определяется в виде
Aα ={x | μA (x) > α} .
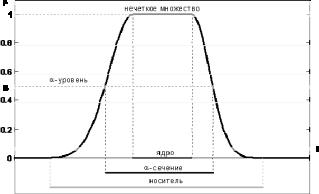
Для произвольной непрерывной функции принадлежности, задающей некоторое нечеткое множество, на рис. 7.5 показаны ядро, носитель и α-сечение.
Рис. 7.5
253