Теорема 6.7 (Дирака). Если в простом графе с n вершинами, причем n ≥ 3, выполняется условие ρ(v) ≥ n 2 для любой верши-
ны v, то граф G является гамильтоновым.
Теорема 6.8 (Оре). Пусть n - количество вершин в данном графе. Если для любой пары несмежных вершин vi, vj выполнено неравенство d(vi) + d(vj) ≥ n, то граф является гамильтоновым.
Однако существуют и гамильнотовы графы, не являющиеся графами Оре или Дирака.
В некоторых задачах дополнительно используется условие Поша, которое в данном пособии не рассматривается.
6.5. Диаметр графа
6.5.1. Основные определения
Расстоянием d между вершинами vi и vj называется длина минимального пути между этими вершинами.
Диаметром δ связного графа G называется максимальное возможное расстояние между любыми двумя его вершинами.
Для несвязных графов диаметр полагается равным бесконечности.
Центром графа G называется такая вершина v, что максимальное расстояние между v и любой другой вершиной является наименьшим из всех возможных. Это расстояние называется радиусом r. Таким образом,
r = min(max d (v1 , v2 )) , |
|
v1 |
v2 |
где d (v1 , v2 ) – расстояние между v1 и v2.
6.5.2. Алгоритм нахождения диаметра
Процесс нахождения диаметра графа представляет собой, по сути, полный перебор.
170
Сначала необходимо по всем парам вершин вычислить расстояние, а затем найти максимум из этого множества чисел.
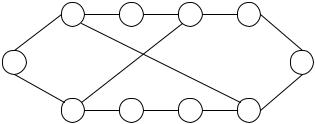
Задача 6.6. Для графа на рис. 6.25 соответствующие расстояния представлены в табл. 6.5.
|
2 |
3 |
4 |
5 |
|
1 |
|
|
6 |
Рис. 6.25 |
10 |
9 |
8 |
7 |
|
|
|
|
Решение. Представлено в табл. 6.5.
|
|
|
|
|
|
|
|
|
|
Таблица 6.5 |
||
|
|
|
|
Матрица расстояний |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
|
1 |
|
1 |
2 |
2 |
3 |
3 |
2 |
3 |
2 |
|
1 |
|
2 |
|
|
1 |
2 |
3 |
2 |
1 |
2 |
3 |
|
2 |
|
3 |
|
|
|
1 |
2 |
3 |
2 |
3 |
3 |
|
2 |
|
4 |
|
|
|
|
1 |
2 |
3 |
3 |
2 |
|
1 |
|
5 |
|
|
|
|
|
1 |
2 |
3 |
3 |
|
2 |
|
6 |
|
|
|
|
|
|
1 |
2 |
3 |
|
3 |
|
7 |
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
8 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
9 |
|
|
|
|
|
|
|
|
|
|
1 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
Необходимо быть аккуратным при вычислении расстояний, например, расстояние между 1-й и 4-й вершинами равно двум, так как помимо пути (1-2-3-4), имеющего длину 3, также существует путь (1-10-4), имеющий длину 2.
Среди всех значений согласно определению диаметра выбирается наибольшее, в данном случае диаметр равен трем.
171
6.5.3. Поиск диаметра при операциях над графами
При операциях над графами иногда значение диаметра проще найти, рассматривая по отдельности участвующие в операциях графы. При этом всегда надо помнить, что диаметр любого несвязного графа равен бесконечности.
При операциях объединения по этой причине в случае отсутствия общих вершин диаметр равен всегда бесконечности. При наличии одной общей вершины значение диаметра вычисляется как сумма диаметров двух участвующих в объединении графов. В более сложных случаях необходимо рисовать полученный граф и анализировать его. Важно помнить, что если в задаче не указано, сколько общих вершин имеют объединяемые графы, то необходимо рассматривать все случаи.
Задача 6.7. Найти значение диаметра графа, полученного в результате объединения простого цикла на 7 вершинах и полного графа на 5 вершинах, если известно, что они имеют 1 общую вершину.
Решение. См. рис. 6.26.
3 |
1 |
Рис. 6.26 |
|
|
Диаметр простого цикла на 7 вершинах равен [7/2] = 3, а диаметр полного графа всегда равен 1. Значит, диаметр полученного в результате объединения графа равен 3+1 = 4.
При операциях сложения двух графов в случае отсутствия общих вершин диаметр всегда будет не более двух. Это связано с тем, что
172