Грушин Повторителный цикл по физике Сборник задач для 11 класса 2011

02.7.Во сколько раз и в какую сторону отличаются центрост-

ремительные ускорения точек земной поверхности на экваторе и в Петербурге (широта υ = 60°)?

02.8.Две материальные точки движутся по окружности радиу-

сом R с угловыми скоростями ω1 и ω2. Чему равно расстояние r между ними через время τ после начала движения, если в начале движения их положения совпадали?

02.9.Автомобиль движется равномерно по прямой дороге со скоростью 20 м/с. Диаметр его колес 75см. Какова скорость верхней точки колеса?

3.ЗАКОНЫ НЬЮТОНА

3.1.На верхний конец вертикальной жесткой штанги, движущейся с горизонтальным ускорением а = 6,5 м/с2, надета муфта массой m = 900 г. С какой силой F муфта действует на штангу?

3.2.На нити подвешены два тела одинаковой массы, соединенные упругой пружиной (рис. 3.1). Нить перерезают. Чему равны

Рис. 3.3

ускорения верхнего и нижнего тел аВ и аН сразу после перерезания нити?

3.3. На гладкой грани призмы с помощью тонкой нерастяжимой нити укреплен брусок (рис.3.2). Брусок начинает скользить вверх,

11

же нитью (рис. 3.5). Сила, с которой нижнее тело действует на нить, равна F=15 Н. Какова сила натяжения верхней нити?

3.10.Два груза массами m1 = 1 кг и т2=2 кг, связанные легкой нитью, подвешены к пружине (рис. 3.6). В некоторый момент нить пережигают. Каково ускорение груза m1 сразу после этого?

3.11.Первая космическая скорость на некоторой планете V 1. Чему равна скорость, необходимая для запуска искусственного спутника планеты с высоты над ее поверхностью, равной радиусу планеты?

3.12.Искусственный спутник массой m движется с включенным двигателем с постоянной скоростью V по круговой орбите вокруг планеты массой М. Радиус орбиты спутника в п раз превышает радиус той орбиты, по которой спутник мог бы двигаться с той же скоростью с выключенным двигателем. Чему равна и как направлена сила тяги, которую развивает двигатель спутника?

3.13.Каков должен быть период вращения Земли Т вокруг

своей оси, чтобы нить математического маятника в равновесии была параллельна оси вращения Земли на широте Москвы (υ = 56º)?

3.14.На доске массой М =1 кг, находящейся на горизонталь-

горизонту. Каково ускорение те-

ла? Коэффициент трения между всеми поверхностями k =0,6.

3.16.Брусок массой m = 500 г соскальзывает с призмы массой

М= 800 г по грани, образующей угол α = 30° с горизонтальной поверхностью, на которой находится призма. Пренебрегая силами

трения, найти ускорение призмы а и величину ускорения бруска относительно призмы аотн.

13

3.17.Веревка длиной L = 12 м и массой m = 6 кг переброшена через блок малого радиуса так, что вначале обе ее половинки расположены чуть несимметрично относительно оси. Чему равно натяжение F в середине веревки в тот момент, когда длина веревки

по одну сторону блока равна L1 = 8 м? Массой блока и трением пренебречь.

3.18.Двигатель запускаемого с Земли реактивного снаряда работает время τ, создавая постоянную по величине и направлению

силу тяги F и обеспечивая прямолинейное движение снаряда под углом α к горизонту. Определить высоту h, на которой прекращается работа двигателя. Изменением массы снаряда и сопротивлени-

ем воздуха пренебречь.

***

03.1.На материальную точку действует постоянная сила. По какой траектории может двигаться точка?

03.2.На рис. 3.9 изображены легкая растянутая пружина, два

бруска, горизонтальная поверхность. Нижний брусок движется с постоянной скоростью. Трение между нижним бруском и поверхностью мало. Как направлено ускорение верхнего бруска?

Рис. 3.9 03.3. Тело массой m, брошенное под углом к горизонту, имеет в верхней точке траектории ускорение а = 4 g/3 (g − ускорение свободного падения). Чему

равна сила сопротивления воздуха?

03.4. Два бруска массами т и 2т, соединенные легкой пружинкой, движутся по гладкой горизонтальной поверхности. В некоторый момент ускорение а1 легкого бруска направлено вправо. Найти

ускорение a2 , с которым в этот момент движется другой брусок.

Растянута или сжата пружинка в этот момент?

03.5. Брусок массой 0,5 кг прижат к вертикальной стене силой 10 H, направленной горизонтально. Коэффициент трения скольжения между бруском и стеной равен 0,4. Какую минимальную силу надо приложить к бруску по вертикали, чтобы равномерно поднимать его вертикально вверх?

14

03.6. Луна действует на Землю с силой F1 . Земля действует на

Луну с силой F 2 . Отношение масс Земли и Луны равно μ. Какова связь между этими силами?

03.7.Тело вблизи поверхности Земли находится в состоянии невесомости. Как оно движется относительно Земли?

03.8.Масса и радиус Марса меньше массы и радиуса Земли соответственно в 10 и 2 раза. На космонавта, находящегося на Марсе, действует сила притяжения 400 Н. Какая сила притяжения будет действовать на него на Земле?

03.9.Какие силы действуют на космонавта, плавающего в кабине космической станции, движущейся по орбите вокруг Земли?

03.10.Небольшая шайба массой m лежит на диске, вращающемся с угловой скоростью ω вокруг вертикальной оси, проходящей через центр диска. Расстояние от шайбы до оси вращения R, коэффициент трения между шайбой и диском μ. Каково максимальное значение угловой скорости ω, при котором шайба еще будет находиться на диске?

4.РАБОТА И ЭНЕРГИЯ. ИМПУЛЬС

4.1.Вверх по наклонной плоскости от ее нижнего края начинает двигаться тело с начальной скоростью V 0 = 10 м/с. На каком расстоянии s от нижнего края плоскости кинетическая энергия тела уменьшится в п = 2 раза? Коэффициент трения между телом

иплоскостью μ = 0,6, угол наклона плоскости к горизонту α = 60°.

4.2.Шар массой т = 1 кг подвесили на пружину жесткостью k = 100 Н/м. Затем шар приподняли так, что пружина оказалась в

недеформированном состоянии, и отпустили. Найти максимальную скорость шара.

4.3.От груза массой М, висящего на пружине жесткостью k, отделилась его часть массой т. На какую максимальную высоту Н после этого поднимется основная часть груза?

4.4.Тело массой m = 1 кг вращается на нити в вертикальной плоскости. При этом в верхней точке траектории сила натяжения

нити T = 10 Н. Чему равна сила натяжения нити в нижней точке траектории?

15

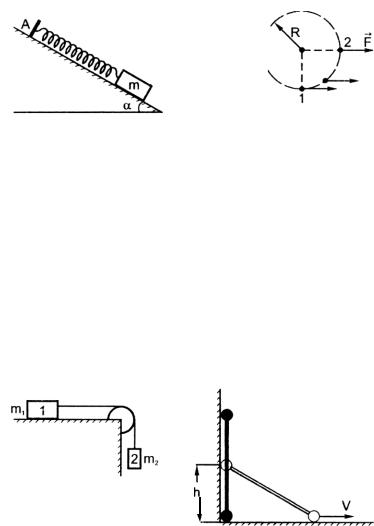
4.5. На наклонной плоскости с углом α находится кубик. К кубику прикреплена легкая пружина, другой конец которой закреплен в неподвижной точке А. Вначале кубик удерживается в положении, при котором пружина не деформирована (рис. 4.1). Кубик отпускают без начальной скорости. Определить макси-

Рис. 4.1 Рис. 4.2

мальную скорость Vm кубика в процессе движения. Масса кубика m, жесткость пружины k, коэффициент трения кубика о наклонную плоскость μ (μ < tg α).

4.6. Небольшое тело массой m движется в горизонтальной плоскости по окружности радиусом R (рис. 4.2). В точке 1 на него начала действовать постоянная по величине и направлению сила F. Пренебрегая трением, найти скорость тела в точке 2, если в точке 1 скорость была равной V 0 .

4.7. На гладком горизонтальном столе лежит доска массой М = 2 кг, на доске − брусок массой т = 1кг. Бруску сообщили горизонтальную скорость V0 = 2 м/с. Какой путь s относительно доски пройдет брусок, если коэффициент трения между ними μ = 0,2?

4.8. Если в системе, изображенной на рис. 4.3, толкнуть брусок 2 вниз, сообщив ему некоторую скорость, то он опустится на рас-

Рис. 3

Рис. 4.

Рис. 4.4

16

стояние h1 = 20 см. Если толкнуть брусок 1 влево (сообщив ему ту же скорость), то он переместится на расстояние h2 = 10 см. Определить коэффициент трения между бруском 1 и поверхностью, по которой он движется, если отношение масс брусков равно

η= т 1 / т2 = 5.

4.9.Какую мощность затрачивает человек на движение саней,

если он их тянет в гору равномерно со скоростью V = 0,5 м/с? Масса саней m = 10 кг, коэффициент трения между полозьями саней и поверхностью горы μ = 0,1. Угол наклона горы α = 30°. Веревка, за которую привязаны сани, натянута под углом β = 45° к поверхности горы.

4.10.Два одинаковых маленьких шарика соединены жестким легким стержнем длиной L = 60 см. Стержень стоит вплотную к вертикальной плоскости (рис. 4.4). При смещении нижнего шарика вправо на малое расстояние система приходит в движение в плос-

кости рисунка. Найти скорость движения нижнего шарика V в момент времени, когда верхний шарик находится на высоте h = 40 см над горизонтальной плоскостью. Считать, что при движении шарики не отрываются от плоскостей, трением пренебречь.

4.11.Тело массой m = 0,2 кг брошено с начальной скоростью V0 = 50 м/с под углом α = 30° к горизонту. Найти модуль изменения импульса: а) за все время полета; б) за половину времени полета. Сопротивление воздуха не учитывать.

4.12.Кусок пластилина массой m = 0,2 кг, брошенный верти-

кально вверх, перед ударом о потолок двигался со скоростью V = 9,8 м/с. Деформируясь при ударе, пластилин прилипает к потолку и принимает окончательную форму через τ = 0,18 с. Найти среднюю силу давления <F> куска пластилина на потолок при ударе.

4.13. На гладкой горке 1, которая находится на гладкой горизонтальной поверхности, лежит шайба 2 (рис. 4.5). Определить,

17

какую минимальную скорость V0 следует сообщить шайбе, чтобы

она поднялась на вершину горки высотой h = 0,5м. Отношение масс шайбы и горки η = m/М = 0,2.

4.14.Тело массой М = 0,1 кг, способное двигаться без трения по

горизонтальному стержню, закреплено на легкой пружине с жесткостью k = 1 кН/м (рис. 4.6). В тело попадает пуля массой m = 10 г,

двигавшаяся под углом α = 60° к оси стержня и застревает в нем. В результате тело начинает колебаться с амплитудой А = 5 см. Определить скорость пули V.

4.15.Бруски массами m1 = 0,1 кг и m2 = 0,4 г находятся на гладкой горизонтальной поверхности и связаны нитью, продетой через пружину жесткостью k = 0,1 кН/м. При натянутой нити пружина

сжата вдвое относительно длины L0 = 10 см в недеформированном состоянии. Найти максимальные скорости V1 и V2 брусков после пережигания нити.

4.16.Пушка стреляет под углом α = 60° к горизонту. Когда колеса пушки закреплены, скорость снаряда V1 = 400 м/с. Когда пуш-

ка может свободно откатываться, ее скорость после выстрела u = 4 м/с. Определить скорость V2 снаряда относительно поверхности при выстреле в последнем случае.

4.17.Тело массой m1 = 1 кг ударяется неупруго о покоящееся тело массой m2 = 2 кг. После удара тела движутся вместе поступательно. Какая часть η кинетической энергии теряется при этом ударе?

4.18.Два шара покоятся, касаясь друг друга. Третий шар нале-

упругий удар. Найти скорости шаров после соударения, если скорость налетающего шара V0 = 1 м/с?

4.19.Шарики массами m и М соединены легкой недеформированной пружиной. Шарику массой m сообщили скорость V в направлении второго шарика. В момент максимального растяжения пружина порвалась. Какое количество теплоты выделилось к этому моменту?

4.20.Между двумя кубиками, массы которых m и М, находится сжатая пружина. Если кубик массой М удерживать на месте, a

18

другой кубик отпустить, то он отлетит со скоростью V. С какой

скоростью V1 будет двигаться кубик массой m, если оба кубика

отпустить? Трением и массой пружины пренебречь.

***

04.1.Тело массой m брошено с горизонтальной поверхности

со скоростью V под углом α к горизонту. Чему равен модуль изменения импульса за все время полета?

04.2.Какие значения может принимать сумма потенциальной

икинетической энергии движущегося тела?

04.3.Потенциальная энергия взаимодействия с Землей гири массой 5 кг увеличилась на 75 Дж. Как переместили гирю?

04.4.Два автомобиля одинаковой массы m движутся со скоро-

стями V и 2V относительно Земли по одной прямой в противоположных направлениях. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем?

04.5.Шарик А налетает на неподвижный шарик В и после удара движется с вдвое меньшей скоростью в направлении, перпендикулярном к первоначальному. Определить угол между первоначальной скоростью шарика А и скоростью шарика В после удара. Зависит ли ответ от вида удара (упругий или неупругий)?

04.6.Тело массой 1 кг брошено с горизонтальной поверхности со скоростью 4 м/с под углом к горизонту и падает на поверх-

ность со скоростью 2 м/с. Чему равна работа сил сопротивления воздуха?

04.7.Деревянная массивная мишень толщиной d =15 см удаля-

ется от стрелка со скоростью V0 = 50 м/с. Пуля массой m = 10 г ле-

тит со скоростью V1 = 300 м/с, пробивает мишень и летит дальше со скоростью V2 = 250 м/с. C какой скоростью летит дальше мишень?

04.8.Тело массой m движется равномерно по окружности в вертикальной плоскости со скоростью V. Чему равна мгновенная мощность, развиваемая силой тяжести в верхней точке?

04.9.Тело вращается на нити в вертикальной плоскости по окружности радиусом R. Скорость тела в нижней точке равна V0. Как связана с этим значением скорость V в верхней точке?

19

5.ДИНАМИКА КОЛЕБАНИЙ

5.1.Шарик подвешен на нити и совершает колебания в верти-

кальной плоскости. При прохождении положения равновесия его ускорение равно а0 = 10 м/с2. Чему равно ускорение шарика при

максимальном отклонении от положения равновесия?

5.2. Брусок массой m = 1,6 кг, соединенный с легкой пружинкой жесткостью k = 256 Н/м, подняли на высоту Н = 85 см от пола и отпустили (рис. 5.1). Длина недеформированной пружины l0 = 50 см. Найти максимальную скорость бруска. Ось пружины во время движения системы остается вертикальной, влиянием воздуха пренебречь.

5.3. К легкой вертикальной пружине с закреплѐнным верхним концом, жесткость которой k, а длина в свободном состоянии L0, подвешивают груз массой М к нижнему концу, а затем груз массой m к середине. Определить длину пружины в равновесии.

5.4. Два одинаковых маленьких пластилиновых шарика подвешены к одному крючку на одинаковых нерастяжимых нитях. Один шарик отклоняют от положения равновесия так, что нить становится горизонтальной, и отпускают. При соударении шарики слипаются. Найти максимальный угол α, на который отклоняется нить после соударения.

5.5. Коробка массой М стоит на горизонтальном столе. В коробке на пружине жесткостью k подвешен груз массой m (рис.5.2). При какой амплитуде колебаний груза m коробка начнет подпрыгивать на столе?

ную стальную плиту, которой шарик абсолютно упруго отскакивает. Время удара пренебрежимо мало. Каким станет период колебаний шарика?

20