Болятко Основы екологии и охраны окружаюсчей 2008

Г Л А В А 5

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОСФЕРНЫХ ПРОЦЕССОВ

5.1. Экологический прогноз и моделирование (классификация моделей)

В современной экологии математическое моделирование играет важную роль. Математические модели - это язык, на котором формулируются наши представления о явлениях в живой и неживой природе, в изучении и моделировании живых систем, которые по своей природе являются открытыми для потоков вещества и энергии. С помощью математической модели можно формализовать и обобщать представление о свойствах и характеристиках сложной системы. Использование моделей является полезным и плодотворным методическим приемом в экологии и природопользовании.

Фундамент математической экологии – математическая теория динамики популяции.

Хорошо известны модели роста популяций, которые основаны на предположении пропорциональности скорости роста численности популяции. Впервые такое поведение популяции было описано Томасом Мальтусом (1798 г.) в виде закона о неограниченном экспоненциальном росте:

скорость роста, часто выражается в процентах за год.

Для большинства популяций существуют ограничивающие факторы, при которых рост прекращается. Единственным исключением является человеческая популяция, которая на протяжении исторического времени растет даже быстрее, чем по экспоненте.

Закон роста населения планеты до середины XX в. хорошо описывался гиперболой, являющейся решением уравнения:

131

в котором скорость роста населения Земли пропорциональна квадрату его численности, а C – определяющий коэффициент. Решением уравнения (5.2) является зависимость, определяющая гиперболический рост населения:

где t0 – момент времени, когда население мира стало бы бесконечным, если бы продолжило расти и далее. В данной модели обычно полагают t0 = 2025 год, а C 2 1011 .

Эта формула хорошо согласуется с данными демографии и описывает рост населения в течение приблизительно нескольких десятков тысяч лет. Тем не менее область ее применимости принципиально ограничена как в будущем, так и в прошлом.

Одной из причин ограничения роста может быть недостаток пищи. Базовой моделью, описывающей ограниченный рост, является модель Ферхюльста (1848 г.).

данных условиях численность популяции (потенциальная емкость экологической системы).

Наличие определенной емкости среды, ограничивающей рост популяции, является важной экологической закономерностью. Множитель (1 N / K ) часто называют сопротивлением

окружающей среды. Решение уравнения (5.4) имеет вид:

132

Зависимость численности популяции от времени (5.5) в естественных условиях описывается S-образной логистической кривой, показанной на рис. 5.1. Кривая роста предполагает плавный переход от экспоненциального роста популяции к стационарной фазе.

Рис. 5.1. Кривые роста популяции: а – экспонента; б – логистическая кривая

Использование рассмотренных законов для моделирования взаимодействий между двумя видами было предложено в работе В. Вольтерра, в частности для системы «хищник - жертва» при различных допущениях.

1. Число особей жертвы N1 растет со скоростью r1 , а убыль со скоростью, пропорциональной числу их встреч с хищником N2 .

Наоборот, популяция хищника увеличивается за счет этих встреч, а убыль происходит только в результате естественной смерти. Тогда:

счет съеденных ими жертв; d2 - коэффициент смертности хищника.

133

Из решения (5.6) вытекает, что система «хищник - жертва» совершает периодические колебания вокруг положения равновесия, а средняя численность популяций за период колебаний равна их равновесному значению.

2. Более реальный случай, когда жертва и хищник

3. Если учесть предельное число жертв, которые хищник в состоянии потребить, и за счет этого сокращение гибели жертвы, то этот предел приблизится к фактору насыщения C , тогда:

Система (5.8) описывает взаимодействия, которые в большинстве случаев будут иметь устойчивую точку равновесия или колебаться в устойчивом предельном цикле в зависимости от величины входящих коэффициентов. Изменение системы по сравнению с рассмотренной моделью будет приводить либо к возникновению устойчивых состояний, либо к ее дестабилизации.

Т. Мальтус противопоставлял модным в начале XIX в. оптимистическим идеям гуманистов, предсказывающих человечеству грядущее счастье и процветание. Он стал первым ученым, который на основании результатов моделирования предупреждал человечество об опасности, связанной с противоречием быстрого роста населения планеты и недостатком продуктов питания.

134

Во второй половине XX в. такую же роль сыграли работы Римского клуба и, в первую очередь, «модель глобального роста» Дж. Форрестера.

При построении модели экосистем применяют методы общесистемного анализа. В первую очередь это – выделение таких отдельных структурных элементов, как живые и косные компоненты, затем среди живых – трофические уровни, виды, возрастные группы и другие, взаимодействие которых и будет определять поведение всей системы.

Любая экосистема состоит из нелинейно взаимодействующих подсистем, которые можно упорядочить в некоторую иерархическую структуру. По мере объединения компонентов в более крупные функциональные единицы у них возникают новые свойства, отсутствующие у составляющих его компонентов.

Особенно быстро развивается направление имитационного моделирования, позволяющее воспроизводить поведение сложных систем, исходя из представлений о свойствах и законах взаимодействия их элементов.

Современные математические модели в экологии можно разбить на три класса. Первый – описательные модели, не претендующие на раскрытие механизма описываемого процесса. Второй – модели качественные, которые способны воспроизвести наблюдаемых динамические эффекты в поведении систем. Третий класс – имитационные модели конкретных экологических систем, учитывающие всю имеющуюся информацию об объекте. Работа с имитационной моделью требует знания величин параметров модели, которые могут быть оценены только из наблюдения и эксперимента.

Цель построения таких моделей (детерминированных или вероятностных) – детальное прогнозирование поведения сложных систем. Чем лучше изучена сложная экологическая система, тем более полно может быть обоснована математическая модель.

Особое значение имеют математические модели, в которых рассматриваются глобальные изменения биоты в результате различного рода антропогенных воздействий или изменения климата в результате космических или геофизических причин. Модели мира – математическое моделирование будущего развития

135

человечества, его взаимоотношения с природными ресурсами и биосферой в целом.

Результатом работы, выполненной Римским клубом, стала

построенная на основе идей Дж. Форрестера компьютерная модель World3, описанная в работе Д. Медоуза. В модели Земля была

рассмотрена как единая система, в которой происходят процессы, связанные с ростом населения, индустриализации, продуктов питания, потребления ресурсов и загрязнения окружающей среды.

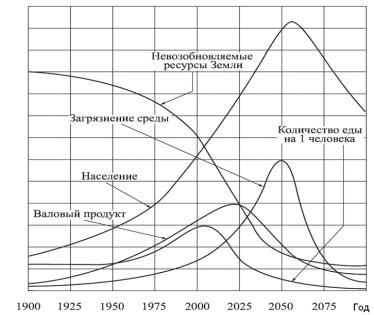
Результаты моделирования привели к печальному выводу (рис. 5.2), что при существующих тенденциях пределы роста на нашей планете будут достигнуты в течение ближайшего времени.

Рис. 5.2. Прогноз развития земной цивилизации при сохранении существующих тенденций развития

Для того, чтобы осуществился сценарий устойчивого развития (рис. 5.3), необходимо принятие программы стабилизации численности населения и объема промышленного производства,

136

уменьшения выбросов загрязняющих веществ и повышения эффективности использования природных ресурсов.

Рис.5.3. Прогноз развития земной цивилизации по программе стабилизации численности населения и по принятым другим мерам

В настоящее время имеются и разрабатываются глобальные модели по прогнозированию изменения климата, расходованию энергии, изменению растительного покрова и др.

5.2. Демографический взрыв

Если современные тенденции мирового развития сохранятся, то в ближайшем будущем человечество окажется в демографической ситуации, в которой на протяжении всей своей истории никогда ранее не существовало. Депопуляция одних народов и стремительный рост численности других, изменение социального статуса института семьи и принципов принятия решения о количестве детей в семье, кардинальное изменение

137

пропорций между городским и сельским населением, между молодыми и пожилыми людьми потребуют от человеческого общества новых культурологических подходов и новых исторических решений.

Необходимо отметить четыре основные тенденции в динамике изменения численности населения планеты в ближайшей перспективе до 2050 г. По мнению большинства экспертов, будет продолжен дальнейший рост численности человеческой популяции. К 2050 г. численность населения Земли увеличится почти на 40%: с настоящих 6,6 до 9,1 – 9,2 млрд чел. Сейчас ежегодно население планеты увеличивается примерно на 80 млн чел., однако ожидается, что темпы прироста численности населения замедлятся, и при этом коренным образом изменится соотношение между городским и сельским населением, а также между количеством пожилых и молодых людей.

Исходя из данных, приведенных в табл. 5.1, легко проследить не только дальнейшее увеличение численности населения мира, но и еще одну наметившуюся уже во второй половине XX в. тенденцию. Значительное смещение демографического баланса между развитыми и развивающимися регионами планеты.

Таблица 5.1

Рост населения мира и темпы прироста с 1950 по 2025 г.

*) БРС – более развитые страны; МРС – менее развитые страны.

138

Если в 1950 г. численность населения в развивающихся странах была примерно вдвое больше, чем в развитых, то к 2050 г. это соотношение может стать шесть к одному.

Прирост населения в ближайшие 45 лет будет фактически полностью происходить в менее развитых странах. При этом почти половина прироста населения планеты будет приходиться всего на девять стран: Индия, Пакистан, Нигерия, Демократическая Республика Конго, Бангладеш, Уганда, США, Эфиопия и Китай. Важнейшей тенденцией динамики населения мира во второй половине XX в. был взрывоподобный рост численности населения развивающихся стран на фоне стабилизации численности населения развитых стран на уровне чуть более 1 млрд чел. Дальнейший рост

численности населения в развитых странах практически прекратился

(рис. 5.4).

Рис. 5.4. Рост численности населения мира

Если в начале нашей эры население планеты оценивалось в 250 млн чел., то его удвоение населения произошло только к 1650 г., а первый миллиардный человек был достигнут в 1830 г. В завершающей стадии индустриальной эпохи развития человеческого общества видится резкий демографический рост.

139

Существенно различаются темпы прироста населения для разных регионов мира. В более развитых странах происходит неуклонное снижение с 1,2% в год до 0,3% в 2000 - 2005 гг. (в Европе с 1,1% в год до 0,1%). В менее развитых странах темпы прироста возрастали до 70-х годов и только затем начали снижаться до величины 1,3% в настоящее время.

Абсолютный ежегодный прирост населения мира около 88 млн чел. был достигнут в 1990 г., а в настоящее время прирост стабилизировался на отметке 74 – 76 млн чел.

Десятку самых многочисленных стран мира сейчас составляют Китай (1,3 млрд жителей), Индия (1,1 млрд), США (300 млн чел.), затем Индонезия, Бразилия, Пакистан, Бангладеш, Россия, Нигерия и Япония. К 2050 г. ожидается, что самой многочисленной страной мира станет Индия. Индия и Китай сохранят существенно опережающие лидирующие позиции, третье место останется за США. Россию и Японию могут обогнать Демократическая Республика Конго и Эфиопия.

Растет средняя продолжительность жизни с 46 лет в 50-х годах, до 64 лет в настоящее время. Ожидается, что к 2050 г. средняя продолжительность жизни возрастет до 75 лет, а в развитых странах до 82 лет. Существенно изменится возрастная структура населения (возрастная пирамида): если в XX в. число молодых людей значительно превышало количество людей старших возрастов, то к середине текущего века численность людей в каждой группе плавно будет перемещаться в последующую возрастную группу.

Доля детей в возрасте до четырех лет неуклонно снижалась во второй половине XX в., а людей старше 60 лет наоборот возрастала. На рубеже веков каждая из этих групп составляла около 10% человечества. Начиная с 2000 г. количество пожилых людей будет превышать число самых юных граждан нашей планеты. Пожилая часть общества составит к 2050 г. уже 22% населения против 11% сейчас. В Европе уже сейчас люди старше 60 лет составляют 21% населения.

Подавляющая часть общего прироста человеческой популяции в ближайшие десятилетия придется на городское население развивающихся стран. Уже в 2008 г. впервые в истории человечества количество горожан и селян сравняется (рис. 5.5).

140