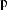Барбашина Мюонная диагностика магнитосферы и атмосферы Земли 2008
.pdf
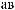
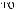
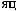


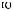 ρ
ρ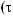
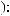
y τ = |
X t X t +τ = n |
∑i= |
(X t − X )(X t +τ − X ) |
|
|
|
|
n |
|
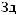
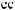

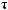

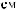

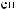

 n
n 

|
|
|
|
|
|
|
|
|
1,0 |
Относительная интенсивность, % |
3.2 |
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
Коэффициент корреляции |
||
3.0 |
|
|
|
|
а) |
|
0,6 |
||
|
|
|
|
|
|
||||
2.8 |
|
|
|
|
|
|
0,4 |
||
|
|
|
|
|
|
|
|||
2.6 |
|
|
|
|
|
|
0,2 |
||
|
|
|
|
|
|
|
|||
2.4 |
|
|
|
|
|
|
0,0 |
||
2.2 |
|
|
|
|
|
|
-0,2 |
||
2.0 |
|
|
|
|
|
|
-0,4 |
||
1.8 |
|
|
|
|
|
|
-0,6 |
||
1.6 |
|
|
|
|
|
|
-0,8 |
||
|
|
|
|
|
|
|
|||
1.4 |
|
|
|
|
|
|
-1,0 |
||
|
|
|
|
|
|
|
|||
|
31 Jan |
2 Feb |
4 Feb |
6 Feb |
8 Feb |
10 Feb |
12 Feb |
14 Feb |
|
|
|
|
|
Дата (2008 год) |
|
|
|
|
|
|
|
|
|
|
б) |
|
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
|
|
|
τ, ч |
|
|
|
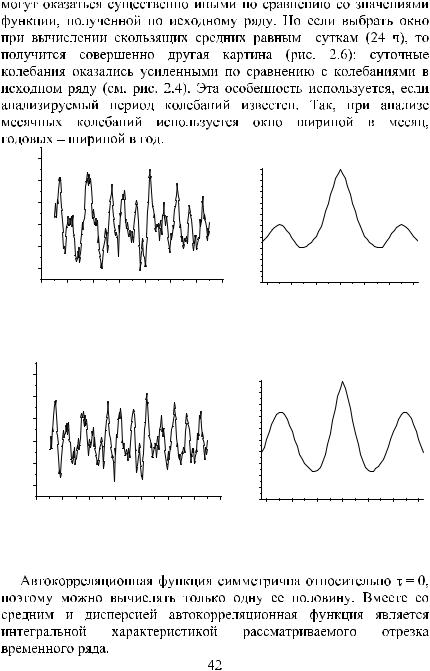
Рис. 2.4. Пример автокорреляционной функции: а) исходный временной ряд относительной интенсивности потока мюонов; б) автокорреляционная функция
% |
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интенсивность, |
|
|
|
|
|
а) |
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0.4 |
|
|
|
|
|
|
|
корреляции |
0.8 |
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0.2 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
||
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Относительная |
|
|
|
|
|
|
|
Коэффициент |
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
||
-0.2 |
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
-0.6 |
|
|
|
|
|
|
||
-0.4 |
|
|
|
|
|
|
|
-0.8 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
-1.0 |
|
|
|
|
|
|
||
|
31 Jan |
2 Feb |
4 Feb |
6 Feb |
8 Feb |
10 Feb |
12 Feb |
14 Feb |
|
|
|
|
|
|
|
|
|
|
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
||||||||
|
|
|
|
Дата (2008 год) |
|
|
|
|
|
|
|
τ, час |
|
|
|
|
Рис. 2.5. Пример автокорреляционной функции: а) временной ряд относительной интенсивности потока мюонов за вычетом тренда с окном 48 ч; б) автокорреляционная функция
% |
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
Относительная интенсивность, |
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
Коэффициент корреляции |
0.8 |
||
0.4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0.6 |
||
0.2 |
|
|
|
|
|
|
0.4 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0.2 |
||
0.0 |
|
|
|
|
|
|
0.0 |
||
|
|
|
|
|
|
|
-0.2 |
||
-0.2 |
|
|
|
|
|
|
-0.4 |
||
|
|
|
|
|
|
|
-0.6 |
||
-0.4 |
|
|
|
|
|
|
-0.8 |
||
|
|
|
|
|
|
|
-1.0 |
||
|
31 Jan |
2 Feb |
4 Feb |
6 Feb |
8 Feb |
10 Feb |
12 Feb |
14 Feb |
|
|
|
Дата (2008 год)
|
|
|
|
|
б) |
|
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
|
|
|
τ, час |
|
|
|
Рис. 2.6. Пример автокорреляционной функции: а) временной ряд относительной интенсивности потока мюонов за вычетом тренда с окном 24 ч; б) автокорреляционная функция

2.2 Частотно-временной анализ
2.2.1 Фурье-преобразование
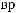
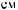
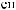
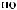
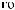
 X(t)
X(t) 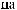
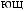
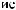
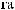
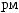

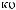
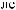
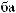

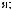
X 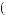 tj
tj 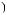 = ∑ak
= ∑ak 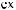
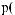 i × wktj
i × wktj 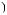
 k =
k = 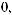
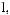 …
… N -
N -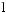

k
wk 
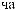
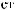
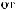
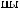
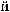
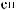
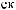
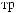
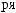
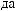 X(tj)
X(tj) ak
ak 
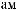
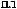

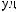

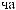
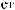
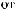 wk
wk N
N
|
|
|
|
X(tj) |
|
ak |
= |
|
∑X tj |
-i × wktj |
|
p |
|||||
|
|
j |
|
X 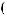 t
t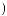 + X
+ X 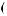 t
t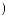 ® a
® a 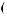 w
w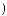 + a
+ a 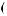 w
w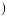
C × X t |
® C × a w |
||
X t ® X t+t |
|||
a w ® |
-i × wt a w |
||
dX t |
dt ® iw× a w |
||
da w dw ® -it × X t |
|||
X(t) |
X(t) |
t – t |
|
a w = |
|
|
-i × wt . |
p |
|||
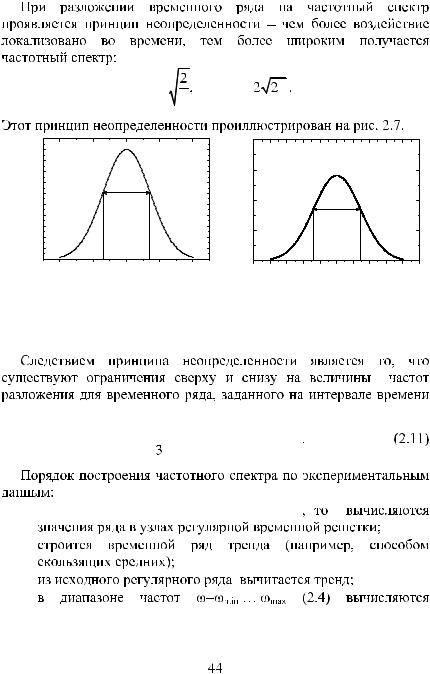
|
|
|
|
|
Dt = |
b |
Dw = |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,1 |
|
|
|
|
|
0,20 |
|
|
|
|
|
|
|
|
|
|
1,0 |
X(t)=exp(-bt2) |
|
|
|
|
F |
2 |
b |
|
b |
1/2 |
) |
|
|
|
|
0,80,9 |
|
|
|
|
а) |
|
(ω)=exp(-ω /(4 |
))/(2(π ) |
|
|
|
||||
|
b=4 |
|
|
|
0,15 |
b=4 |
|
|
|
|
|
|
|
|
||
|
0,7 |
|
|
t=(2/b)1/2 |
|
|
|
|
|
|
|
|
|
б) |
|
|
|
0,50,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
X(t) |
|
|
|
|
|
F(ω) 0,10 |
|
|
b |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω=(8 |
) |
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
|
|
|
|
-1,0 |
-0,5 |
0,0 |
0,5 |
1,0 |
-10 |
-8 -6 |
-4 -2 |
0 |
2 |
4 |
|
6 |
8 |
10 |
|
|
|
|
t |
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
Рис. 2.7. Иллюстрация принципа неопределенности с |
|
|
||||||||||||
ΔtΔω=4 – const: а) временной ряд X(t) в виде колокола с шириной Δt; |
||||||||||||||||
|
|
|
б) частотный спектр F(ω) с шириной Δω |
|
|
|
|
|
||||||||
t = 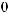 …Tw
…Tw 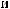
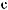
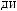
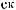

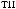
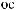
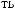
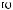
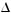 t
t
w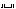 »
» 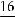 ×
×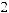 p
p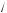 Tw
Tw  w
w
 »
» 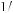 Dt
Dt
· 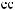
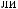
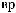
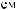
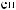
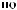
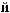
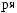
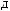 X(t)
X(t) 
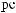
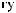
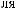
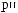
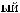
·
· ·
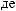
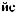
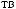

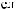
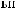
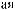
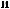

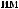
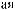
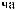
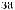 a
a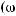
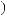

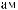
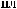

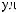
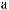 A
A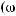
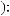
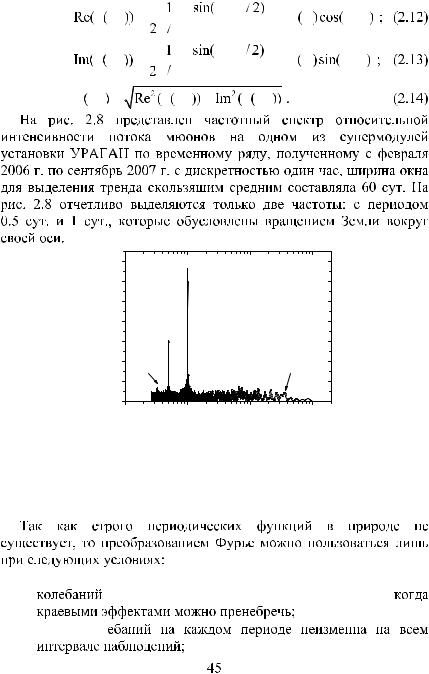
a ωk |
= |
|
|
|
ωk |
t |
∑X tj |
ωktj |
|
|
π ωk |
|
πωk |
|
|||||
|
|
|
|
|
j |
|
|||
a ωk |
= |
|
|
|
ωk |
t |
∑X tj |
ωktj |
|
|
π ωk |
|
πωk |
|
|||||
|
|
|
|
|
j |
|
|||
|
|
|
|
|
|
|
|
||
A ωk = |
|
|
a ωk |
+ |
a ωk |
|
|||
|
14 |
|
|
|
|
|
|
1 |
|
|
12 |
|
сутки |
|
|
|
|
|
|
отн.ед. |
10 |
|
|
|
8 |
1/2 |
|
|
|
|
|
|
||
|
суток |
|
|
|
A, |
6 |
|
|
|
|
4 |
1/3 |
|
35 |
|
суток |
|
|
|
|
|
|
суток |
|
|
2 |
|
|
|
|
0 |
|
|
|
|
0,1 |
1 |
10 |
100 |
|
|
|
Период, сут. |
|
Рис. 2.8. Частотный спектр интенсивности мюонов по данным установки УРАГАН
2.2.2 Вейвлет-преобразование
∙ 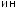

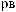
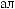
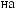

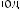

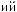









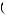 Tw
Tw 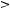
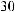 T
T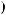

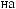
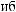
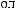
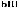

 T
T
∙ 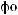
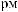

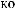


· 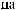
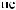
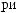
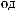 T
T 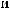


· 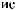
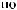
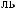
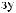
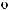

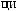
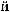
· 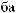
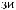
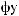

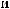 Ψ
Ψ
ψ 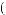 t
t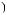 = p−
= p−
 × s−
× s−
 ×
×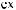
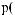 i × w t
i × w t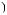 ×
×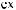
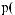 -t
-t
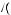
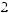 s
s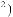
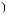
Рис. 2.9. Вейвлет Морле: плоская волна, модулированная гауссианом
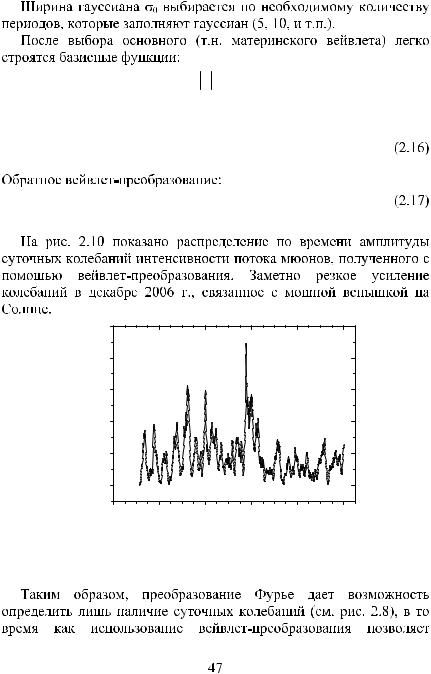
ψab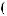 t
t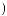 = a −
= a −
 ψ [
ψ [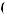 t - b
t - b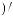 a]
a] 
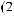
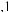
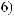
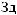
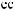
 a
a 
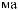
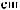
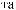
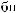
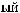
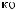
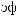
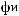
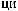

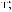 b
b 

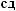

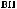
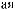
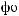
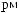
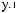
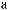
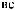
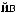
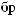


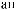
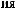
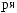
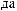 X(t)
X(t)
∞
c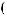 a
a b
b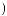 = ∫ X
= ∫ X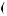 t
t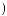 ψab
ψab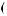 t
t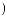 dt
dt 
−∞
X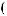 t
t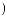 =
= 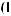
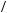 Cψ
Cψ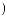 ∫R
∫R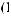
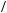 a
a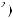 × c
× c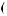 a
a b
b ×ψab
×ψab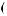 t
t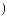 × da × db
× da × db 
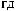
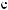 C
C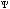


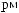
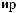
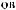

|
250 |
|
|
|
|
|
цикла |
200 |
|
|
|
|
|
|
|
|
|
|
|
|
суточного |
150 |
|
|
|
|
|
100 |
|
|
|
|
|
|
Амплитуда |
50 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Jan |
1 May |
1 Sep |
1 Jan |
1 May |
1 Sep |
|
|
2006 |
|
Дата |
2007 |
|
Рис. 2.10. Динамика изменения амплитуды суточных колебаний интенсивности потока мюонов по данным установки УРАГАН

Достоинства 
 ∙
∙ 

∙ 





∙ 

Недостатком
Контрольные задания
Методы статистического анализа данных в мюонной
диагностике

X(t)
(t ÷ t+Tw) |
|
|
|
|
|
|
|
|
||||||
|
|
|
X(t,Tw ) |
|
||||||||||
D(t,Tw) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Xi |
|
|
|
|
|
|
|
X(t,Tw ) = X = |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n i= |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
D(t,Tw ) = D = |
|
|
|
∑Xi |
− nX |
|
|
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
n -1 i= |
|
|
|
|
|
|
||
n |
|
i |
|
|
Xi |
(t ÷ t+Tw) |
||
|
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
(t ÷ t+Tw) |
|
|
|
|
||||
X(t,Tw ) |
D(t,Tw) |
|||||||
X =  D
D
n
D = |
|
|
|
n |
X |
|
|
|
|
− |
n − |
D |
|
|
|
|
|
− X |
|
||||||||
|
|
|
|
i |
|
|
|||||||
|
|
|
∑ |
|
|
|
|
n − |
|||||
|
n n i= |
|
|
|
|
|
|
|
|||||
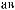
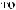
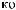
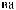
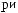
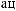
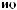
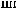
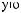


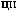
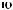 y
y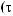

y τ = Cov X t X t+τ = 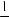 ∑n (X (ti )− X )(X ti +τ − X ) n i=
∑n (X (ti )− X )(X ti +τ − X ) n i=
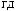
 τ
τ 


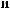
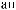
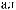
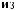

Этапы выполнения работы.

Рис. Л3.1. Вид файла с данными УРАГАН

 .
. 



 .
. 





∙ 

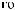
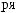
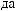

∙ |
|
|
|
|
|
|
|
|
X |
X ± X X ± D |
|||||||
∙ |
|
|
|
|
|
|
|
|
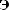



 .
.