
Барбашина Мюонная диагностика магнитосферы и атмосферы Земли 2008
.pdf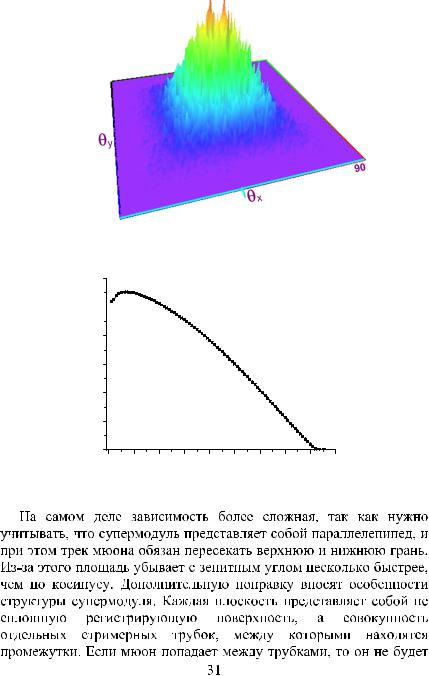
Рис. 1.17. Угловое распределение мюонов, зарегистрированных в течение одной минуты (матрица проекционных углов)
Эффективная площадь, м2
12
10 

8
6
4
2
0
0 10 20 30 40 50 60 70 80 90
θ, o
Рис. 1.18. Эффективная площадь супермодуля годоскопа УРАГАН

Контрольные вопросы

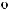
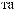
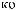
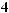 π
π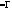
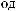
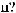
Расчет темпа счета мюонного годоскопа

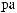

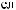
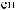
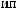
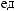
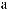
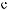
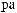
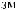
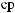

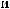 Lx×Ly×Lz
Lx×Ly×Lz 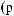
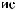


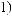

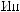


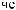
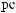
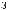

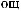
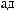
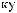 dS
dS 
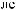
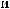
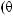
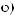
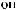

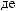
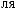
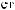
N = ∫∫I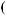 q
q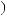 dSdW
dSdW
S Ω
Ι q = I |
q |
I0 |
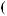 I0=
I0=
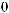
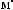
 ×
×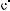
 ×
×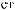
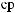

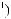
 dW=
dW=
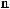 q
q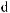 q
q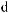 j
j 
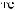
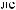
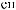
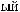
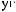
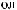

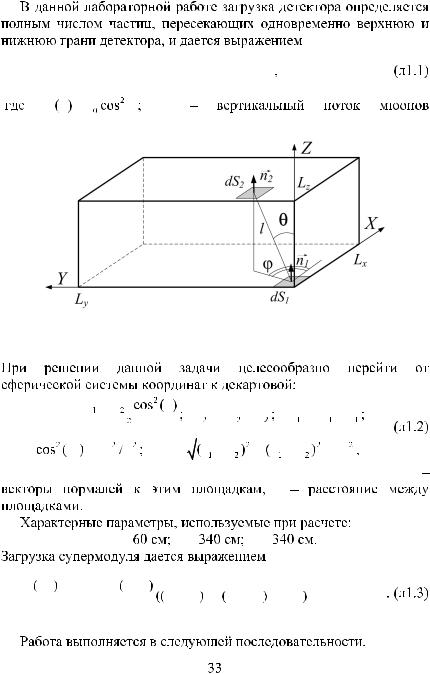
Рис. Л1.1. Схема расчета загрузки супермодуля мюонного годоскопа
dW = |
dS × dS |
× |
q |
dS = dx × dy dS = dx × dy |
|
|
l |
|
|||
|
|
|
|
|
|
|
|
|
|
||
qi = Lz |
li |
li = xi - xi + yi - yi + Lz |
|||
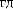
 dW
dW 







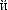
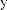



 dS1, dS2
dS1, dS2 







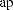






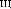
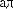


 n1, n2 l
n1, n2 l
|
|
|
Lz |
Lx |
Ly |
|
|
− |
|
Lx Ly Lx Ly |
Lz |
2 |
|
N c |
1 |
= ∫ ∫ ∫ ∫ I Lz l |
|
dx dx dy dy |
||
|
|
|
||||
|
|
0 0 0 0 |
x1 − x2 2 + y1 + y2 2 + Lz2 2 |
|||

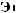

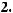
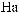
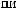
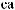
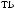
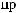
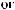
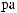

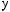
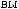
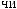
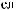
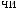
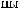
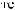
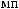
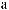
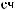
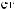
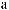 N
N 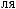
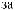
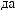
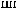
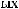
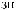
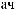
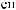
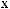
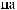
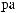
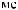
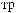
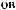 Lx, Ly, Lz
Lx, Ly, Lz
N 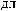

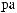
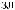
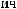
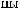
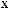
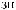
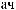
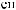
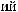 L
L
Lx 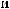 Ly
Ly
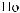
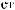
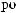


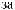
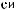
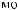
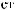
 N = f(Lz)
N = f(Lz)

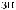

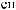
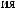 N
N 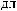

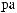
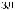
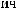
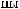
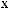
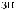
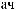
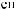
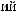 Lx
Lx 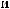 Ly
Ly
L
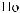
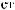


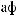
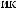
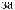
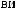
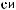
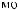
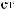
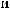 N = f(Lx).
N = f(Lx).
Изучение углового распределения потока мюонов

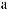 θ
θ 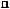
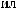
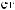
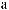
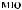

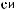
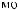
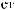

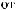
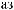
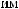
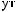
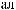
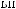
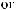
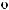
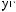
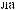 ϕ
ϕ 
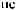
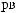

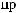
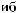
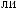
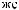
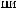
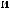
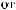
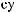
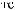


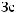

 α θ
α θ 
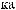

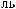

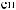
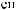
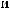 α
α



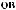 I
I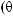
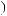
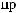
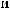
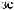
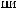
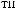
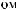
 θ
θ

I q = DN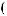 q
q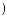
T × e × DSW q
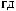
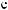 N
N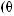
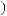


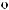
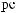



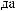

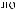
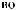

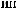
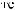
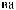
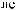 T
T 
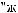

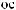


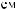


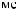
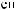
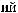

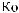
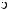
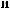


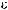
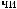
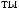
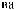
DSW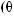
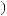
DSW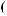 q
q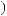 = ∫ S (q¢) dW¢
= ∫ S (q¢) dW¢ 
ΔΩ
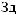
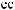
 DW
DW 
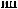
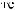
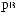
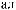
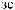
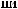
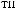
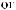
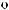
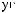
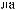

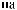
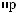
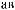
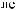
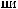
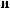 q
q
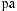
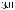
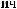
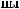
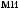
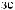
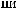
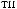
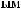
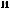
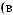
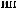
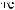
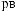
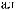
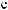
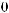 °
° 
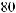 °
° 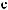
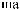
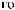
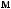
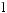 °
°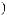
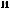

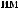
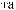
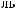
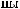
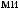
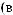
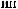
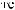
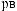
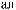
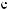
 °
° 
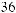
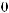 °
° 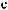
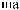
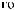
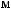
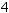 °
°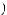
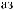
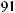 ´
´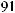
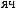
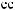
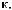
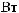
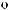
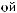
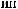
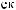
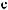

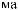
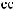

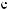
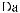
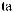
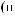
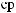
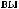
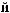
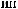
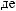


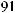 ´
´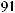

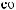
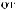
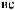

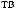

Этапы выполнения работы.

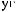
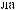 N
N θ
θ

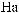
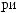
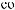
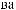
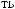
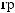
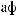
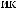
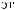

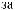

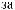
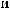
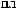
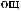
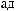
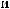
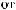
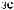
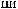
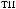
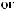
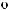
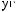
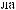 S (q)
S (q) 

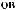
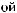
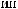
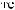
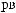
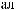 Dq
Dq
DSW(q) » 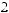 pS (q)×
pS (q)×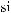
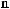 q × Dq
q × Dq 
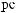
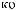
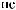
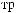

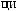
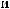 ε ≈
ε ≈ 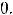
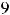

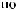
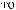
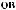
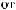
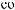
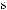 q
q 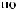
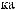
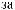
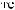
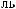
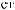
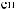
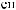
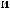 a
a
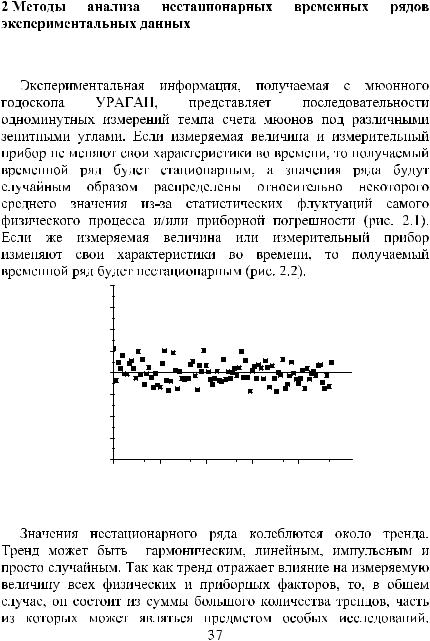
2.1 Основные характеристики временных рядов
Значение
180 |
|
|
|
|
160 |
|
|
|
|
140 |
|
|
|
|
120 |
|
|
|
|
100 |
|
|
|
|
80 |
|
|
|
|
60 |
|
|
|
|
40 |
|
|
|
|
20 |
|
|
|
|
1 Jan |
22 Jan |
12 Feb |
4 Mar |
25 Mar |
Дата
Рис. 2.1. Пример стационарного временного ряда
Значение
180 |
|
|
|
|
|
160 |
|
|
|
|
|
140 |
|
|
|
|
|
120 |
|
|
|
|
|
100 |
|
|
|
|
|
80 |
|
|
|
|
|
60 |
|
|
|
|
|
40 |
|
|
|
|
|
20 |
|
|
|
|
|
1 |
Jan |
22 Jan |
12 Feb |
4 Mar |
25 Mar |
Дата
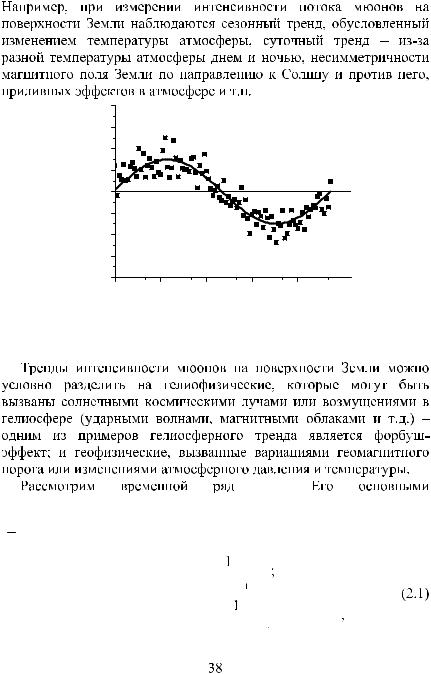
Рис. 2.2. Пример нестационарного временного ряда. Жирной линией изображен тренд
X(t)
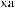
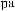
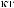
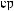
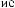
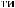
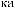
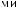
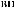
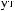
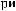
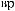
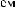
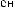
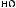
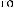
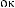
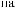

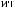
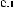
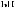
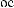
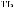
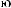 Tw
Tw
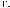



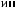
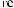
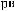
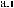

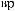
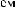
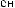

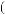 t ÷ t+Tw
t ÷ t+Tw

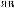
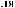
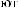
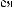
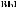
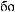
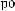
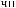
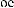

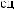
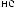

X(t,Tw ) 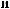
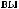
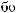
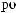
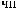
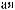
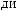
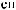
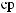
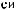
 D(t,Tw)
D(t,Tw)
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Xi |
|
|
|
|
|
|
X(t,Tw ) = X = |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n i= |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
D(t,Tw ) = D = |
|
|
|
∑Xi |
− nX |
|
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
n -1 i= |
|
|
|
|
|
||

n |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi |
(t ÷ t+Tw), |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X(t,Tw ) D(t,Tw) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X = |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
D = |
|
|
|
n |
X |
|
|
|
|
− |
n − |
D |
|
|||||
|
|
|
|
|
|
|
|
|
|
− X |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
n − |
||||||||
|
|
|
|
|
|
|
n n i= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||

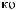
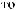
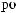
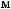
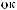

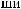
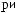
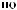
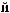 Tw
Tw
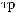
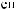
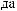 S(t)
S(t)
S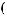 ts
ts  Tw
Tw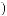 = X
= X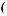 tx
tx Tw
Tw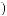

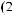
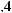
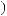
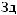
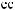
 ts
ts 
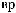

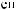
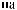

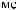
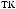
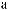
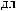

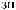
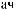
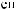
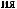
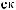
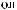
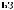

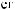
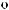
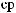
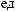

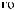
 tx
tx
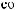
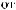
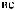
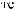

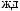
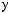 ts
ts 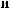 tx
tx
ts = tx 
ts = tx + Tw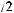
 ts = tx + Tw
ts = tx + Tw 
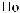
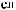
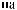
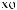
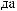 S(t)
S(t) 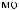
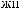
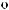
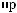
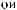
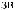
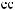
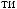
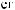
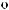
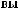
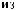
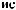
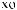
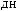
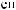
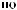
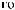
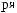
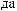 X(t)
X(t) 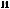

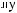
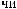
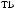
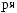
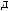
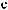
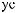
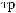
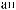
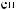
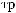
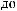
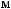 Z(t)
Z(t)
Z(t) = X(t) - S(t)
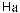
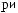
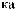
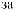

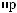
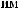
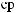

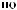
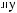
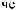
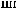
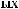
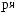
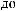
 Z(t)
Z(t) 
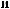
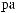
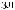
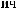
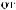
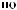

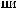
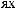
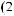
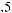
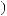
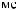
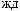
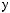 ts
ts 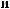 tx
tx



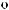
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
а) |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
70 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
Значение |
|
|
|
|
|
|
|
|
Значение |
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
50 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
|
30 |
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Время |
|
|
|
|
|
|
|
|
Время |
|
|
|
|
|
15 |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
10 |
|
|
|
|
г) |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение |
5 |
|
|
|
|
|
|
Значение |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
-15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
-25 |
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
|
|
Время |
|
|
|
|
|
|
|
|
Время |
|
|
|
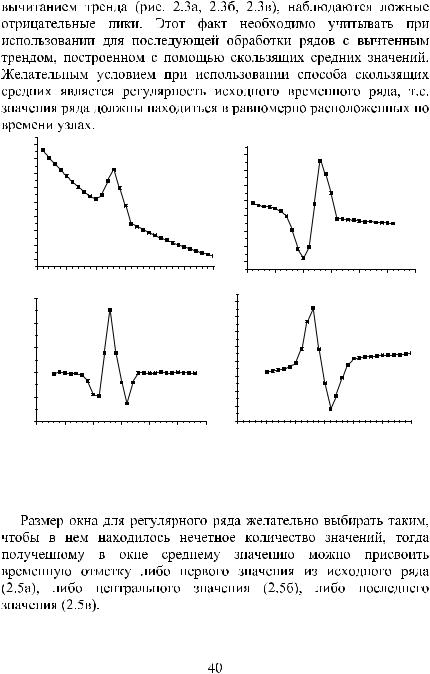
Рис. 2.3. Примеры временных рядов, полученных из исходного ряда а) путем вычитания ряда из скользящих средних с окном Tw=5отн.
ед.; б) с использованием (2.5а); в) (2.5б); г) (2.5в)
