- •5 Расчетно-конструктивная часть
- •5.2 Исходные данные для расчета
- •5.4 Расчет ветровой нагрузки
- •5.5 Расчет здания на вынужденные колебания Сейсмическая нагрузка
- •5.6 Грунтовые условия площадки и выбор параметров упругого основания
- •Выполнение расчета
- •Результаты расчета
- •Подбор арматуры в фундаментной плите
- •5.9 Конструирование армирования: - фундаментной плиты
Выполнение расчета
Расчет конструкций каркаса выполнен на ПЭВМ с использованием вычислительного комплекса «Лира-9.6» в соответствии с действующими в настоящее время строительными нормами и правилами. Вычислительный комплекс реализует метод конечных элементов и предоставляет возможность выполнять расчет на статические и сейсмические нагрузки согласно требованиям СНиП 2.01.07-85*«Нагрузки и воздействия», СНиП II-7-81*«Строительство в сейсмических районах.
В основу расчета положен метод конечных элементов в перемещениях.
Расчетная модель подробно описывает конструктивные решения здания, в том числе с учетом грунтовых условий.
Цель расчета – получение перемещений в остове здания в целом от совместного действия вертикальных и горизонтальных нагрузок для сравнения их с допустимыми перемещениями для такого типа сооружений, а так же получение площадей продольной и поперечной арматуры в элементах каркаса.
Расчетная схема показана на рисунке 5.5.
Нагрузки прикладываем в виде отдельных загружений:
1 Постоянная нагрузка (собственный вес с учетом конструкций пола);
2 Временная (полезная нагрузка);
3 Временная (снеговая нагрузка);
4 Ветровая нагрузка вдоль буквенных осей (ось X);
5 Ветровая нагрузка вдоль числовых осей (ось Y);
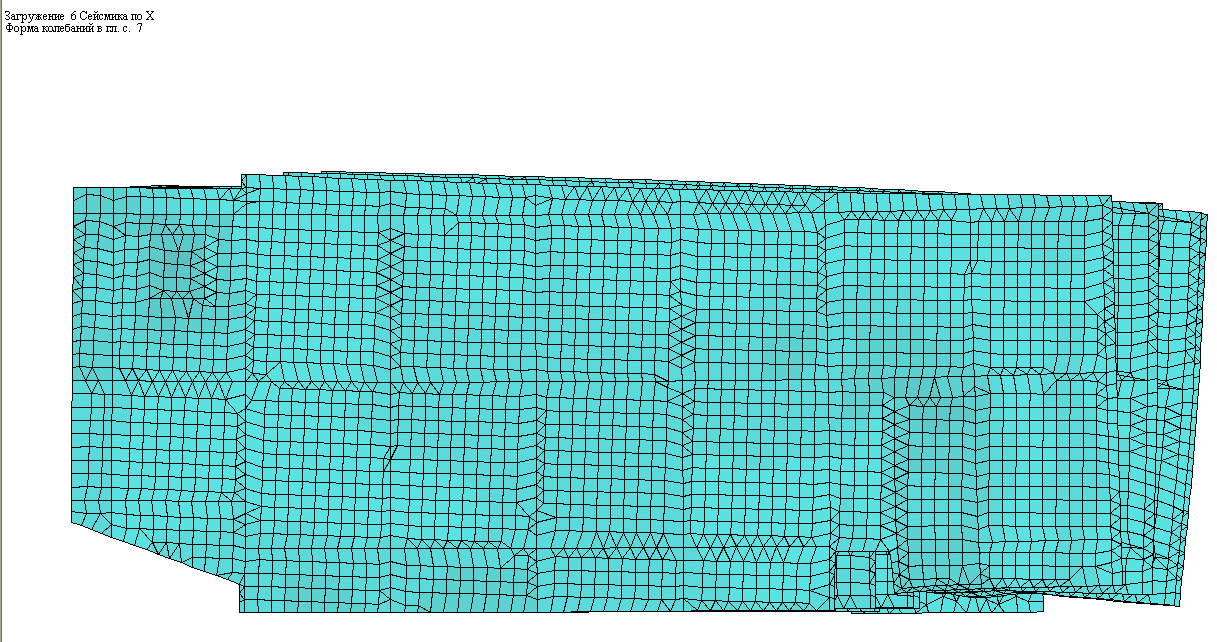
6 Сейсмическая нагрузка вдоль буквенных осей (ось X);
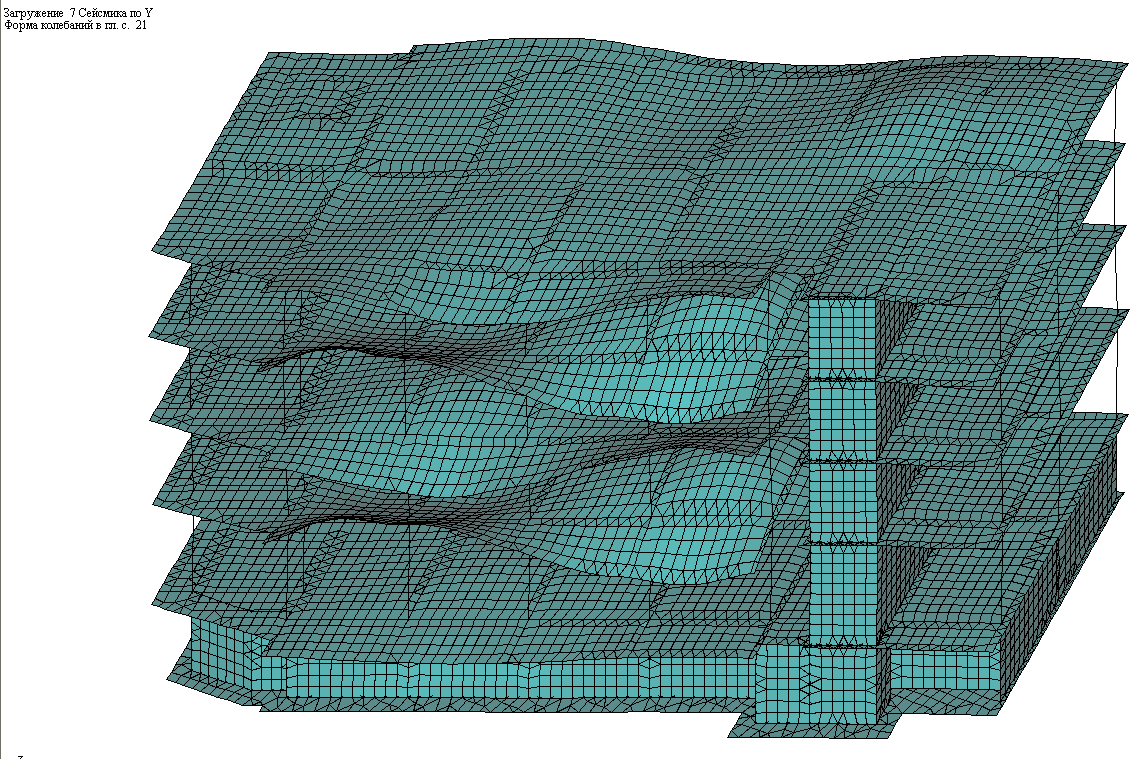
7 Сейсмическая нагрузка вдоль буквенных осей (ось Y);
с автоматическим выбором наиболее опасного направления и с учетом угловых ускорений (кручение).
Определяем наиболее опасные комбинации загружений для каждого элемента, используя механизм РСУ и РСН программы «Лира».

Рис. 5.6 – Расчетное сочетание усилий

Рис. 5.7 – Задание расчетных сочетаний нагрузок
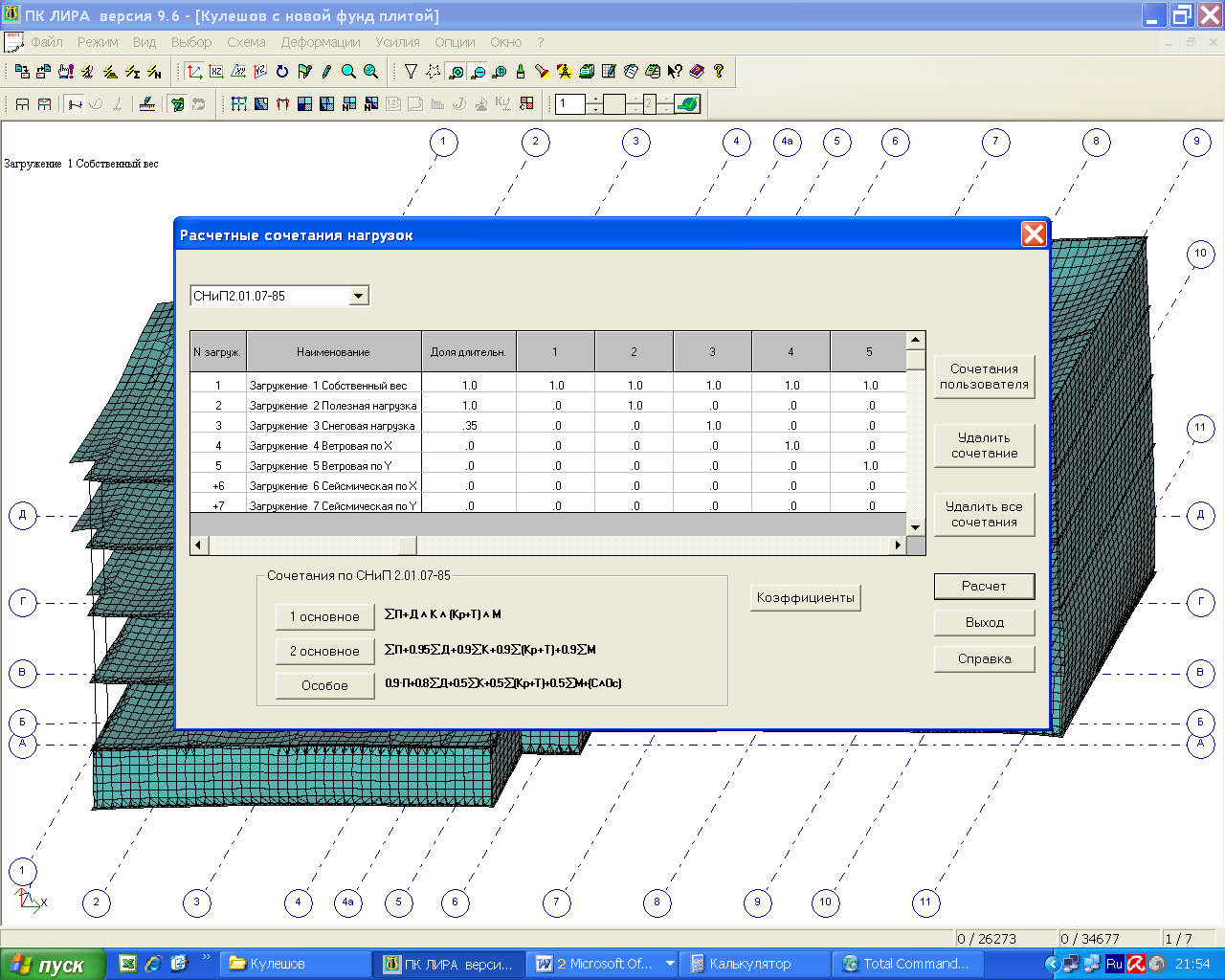
Рис. 5.8 – Расчетное сочетание нагрузок с 1 по 5 сочетание
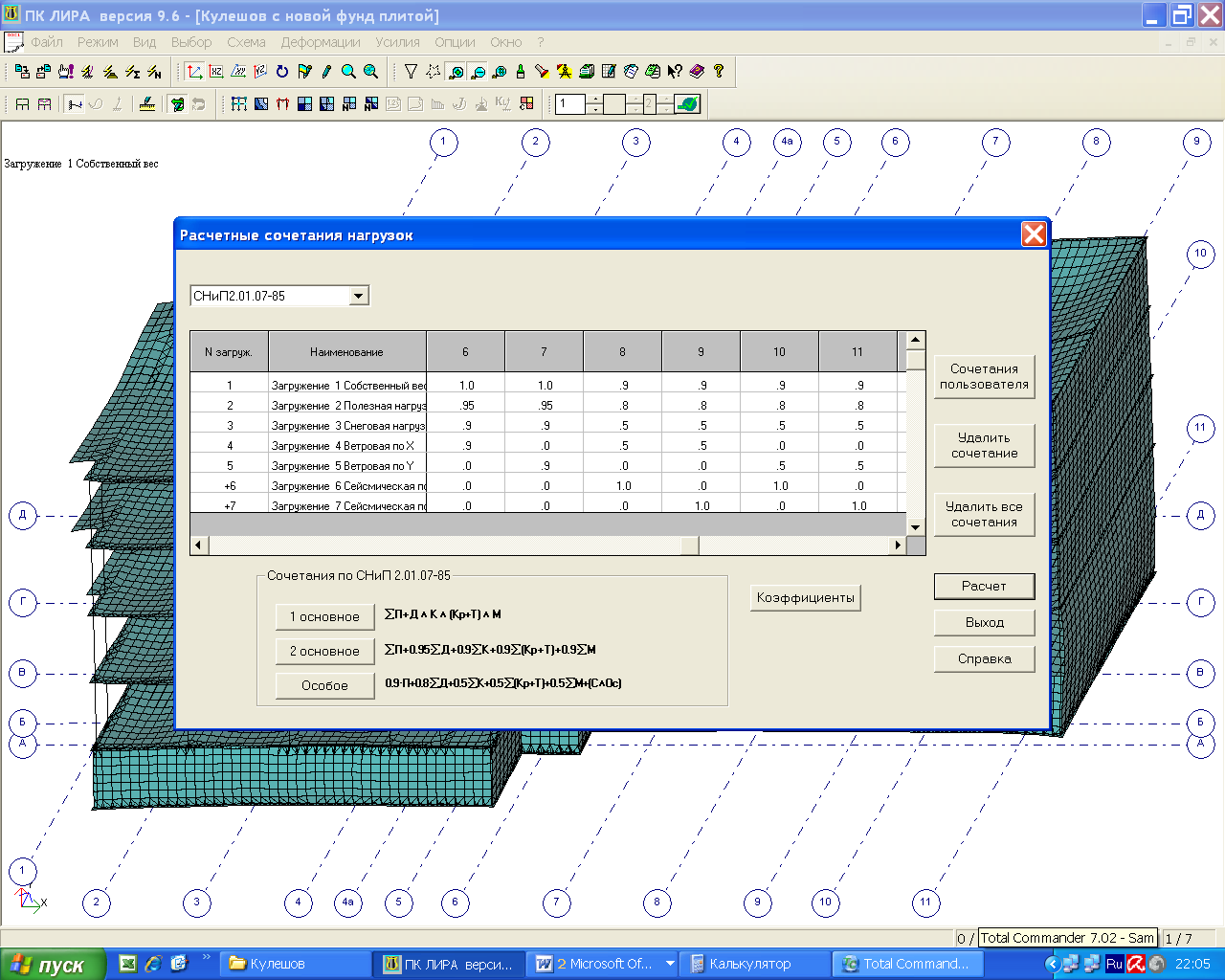
Рис. 5.9 – Расчетное сочетание нагрузок с 6 по 11 сочетание

Рис. 5.10 – Расчетное сочетание нагрузок с 10 по 15 сочетание
В расчете на динамические нагрузки использован режим с автоматическим определением наиболее опасного направления сейсмического воздействия по формам колебаний (с учетом кручения). Задано 3 направления сейсмического воздействия - два поступательных и одно вращательное (по направляющим косинусам двух первых форм колебаний) с учетом 25 форм собственных колебаний для каждого воздействия. Величины сосредоточенных масс определены программно путем формирования масс через заданный объемный вес конструкций с учетом постоянных и временных нагрузок.

Рис. 5.11 – Задание характеристик для расчета на динамические воздействия

Рис. 5.12 – Формирование динамических загружений
Результаты расчета
ПРОТОКОЛ РАСЧЕТА от 13/06/2011
Version: 9.6, Processor date: 30/06/2009
Computer: GenuineIntel 2.67GHz, RAM: 2047 MB
Open specifications for Multi-Processing
17:12 65_ Фиксированная память - 1199 МБ, виртуальная память - 1199 МБ.
17:12 173_ Исходные данные.
Файл C:\PROGRAM FILES\LIRA SOFT\LIRA 9.6\LDATA\Анисимова.TXT
17:12 168_ Ввод исходных данных основной схемы.
17:12 10_ Формирование форматов данных.
17:12 466_ Контроль исходных данных _1. Супеpэлемент типа 2000.
17:12 12_ Контроль исходных данных _2. Супеpэлемент типа 2000.
17:12 98_ Из системы уравнений исключено 15184 неизвестных.
X-0. Y-0. Z-0. UX-1811. UY-1383. UZ-11990.
17:12 1_ Данные записаны в файл расчета
C:\PROGRAM FILES\LIRA SOFT\LIRA 9.6\LWORK\Анисимова#00.DXF
17:12 523_ Упоpядочение матpицы жесткости основной схемы.
Постpоение гpафа матpицы.
17:12 210_ Проверка графа матрицы.
17:12 105_ Упорядочение матрицы при помощи алгоритма минимальной степени.
17:12 210_ Проверка графа матрицы.
17:12 562_ Перенумерация в схеме
17:12 520_ Инфоpмация о pасчетной схеме супеpэлемента типа 2000.
- поpядок системы уpавнений 95964
- шиpина ленты 95964
- количество элементов 23303
- количество узлов 18526
- количество загpужений 7
- плотность матpицы 1%
- количество супеpузлов 0
- дисковая память : 112.760 M
17:12 522_ Ресуpсы необходимые для выполнения pасчета
1. Дисковая память : 582.850 M
фоpматы данных 16.000 M
матpица жесткости основной схемы 112.760 M
матpицы жесткости супеpэлементов 0.000 M
динамика (f04) 112.020 M
пеpемещения (f07) 42.465 M
усилия (f08) 44.771 M
pеакции (f09) 0.000 M
pасчетные сочетания (f10) 254.835 M
2. Оpиентиpовочное вpемя pасчета 21.85 мин.
Гаусс 0.92 мин.
динамика 19.15 мин.
pасчетные сочетания 0.98 мин.
устойчивость 0.00 мин.
17:12 575_ Формирование матрицы жесткости основной схемы.
17:13 578_ Разложение матрицы жесткости основной схемы.
Ориентировочное время работы 1 мин.
17:13 39_ Контроль решения основной схемы.
17:13 569_ Накопление масс
17:13 20_ Определение форм колебаний. Загружение 6.
Выбор стартовых векторов.
17:13 536_ Распределение масс для загружения 6
Количество активных масс 95964
| X Y Z UX UY UZ
| 544.198 544.198 544.243 4.27449 4.55430 1.00612
17:13 627_ При определении форм колебаний будет использована матрица масс.
17:13 3_ Итерация 1. Невязка 9.89E+001%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 0. Частота 0.00 Гц.
17:14 3_ Итерация 2. Невязка 2.54E+001%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 0. Частота 0.00 Гц.
17:14 3_ Итерация 3. Невязка 6.89E+000%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 3. Частота 2.21 Гц.
17:14 3_ Итерация 4. Невязка 2.32E+000%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 6. Частота 5.87 Гц.
17:14 3_ Итерация 5. Невязка 7.41E-001%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 9. Частота 6.96 Гц.
17:14 3_ Итерация 6. Невязка 2.14E-001%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 11. Частота 7.61 Гц.
17:15 3_ Итерация 7. Невязка 1.18E-001%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 12. Частота 8.23 Гц.
17:15 3_ Итерация 8. Невязка 4.12E-002%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 15. Частота 9.17 Гц.
17:15 3_ Итерация 9. Невязка 1.32E-002%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 19. Частота 10.01 Гц.
17:15 3_ Итерация 10. Невязка 4.23E-003%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 23. Частота 10.68 Гц.
17:16 3_ Итерация 11. Невязка 1.42E-003%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 24. Частота 10.71 Гц.
17:16 3_ Итерация 12. Невязка 4.85E-004%, точность 1.0E-003%.
Количество фоpм 25. Получено фоpм 25. Частота 10.74 Гц.
17:16 178_ Количество выполненных итераций 12, из них 0 добавочных.
17:16 20_ Определение форм колебаний. Загружение 7.
Выбор стартовых векторов.
17:16 536_ Распределение масс для загружения 7
Количество активных масс 95964
| X Y Z UX UY UZ
| 544.198 544.198 544.243 4.27449 4.55430 1.00612
17:16 627_ При определении форм колебаний будет использована матрица масс.
17:16 567_ Вычисление динамических сил. Загружение 6
17:16 68_ Форма 1. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.28161 0.95952 0.00300
17:16 68_ Форма 2. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.96046 0.27841 0.00340
17:16 68_ Форма 3. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.57139 0.81951 -0.04369
17:16 68_ Форма 4. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.00031 -0.01086 0.99994
17:16 68_ Форма 5. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.38256 0.13588 0.91388
17:16 68_ Форма 6. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.69073 -0.66192 -0.29113
17:16 68_ Форма 7. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.99854 0.05270 0.01155
17:16 68_ Форма 8. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.17115 0.01872 -0.98507
17:16 68_ Форма 9. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.01091 0.99768 0.06716
17:16 68_ Форма 10. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.42499 0.87165 0.24413
17:16 68_ Форма 11. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.03780 -0.57782 -0.81529
17:16 68_ Форма 12. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.26546 0.93464 -0.23661
17:16 68_ Форма 13. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.21240 0.96610 -0.14672
17:16 68_ Форма 14. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.31265 -0.52968 0.78847
17:16 68_ Форма 15. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.09669 -0.69410 0.71336
17:16 68_ Форма 16. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.09700 0.90146 0.42185
17:16 68_ Форма 17. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.08046 -0.99474 -0.06346
17:16 68_ Форма 18. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.51134 0.85633 0.07232
17:16 68_ Форма 19. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.76308 0.56145 -0.32014
17:16 68_ Форма 20. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.65648 -0.75166 0.06357
17:16 68_ Форма 21. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.35034 0.92396 -0.15347
17:16 68_ Форма 22. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.17221 0.97932 -0.10615
17:16 68_ Форма 23. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.92399 -0.37716 0.06322
17:16 68_ Форма 24. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.99850 0.05100 0.01985
17:16 68_ Форма 25. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.05129 -0.98883 0.13993
17:16 567_ Вычисление динамических сил. Загружение 7
17:17 68_ Форма 1. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.28161 0.95952 0.00300
17:17 68_ Форма 2. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.96046 0.27841 0.00340
17:17 68_ Форма 3. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.57139 0.81951 -0.04369
17:17 68_ Форма 4. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.00031 -0.01086 0.99994
17:17 68_ Форма 5. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.38256 0.13588 0.91388
17:17 68_ Форма 6. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.69073 -0.66192 -0.29113
17:17 68_ Форма 7. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.99854 0.05270 0.01155
17:17 68_ Форма 8. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.17115 0.01872 -0.98507
17:17 68_ Форма 9. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.01091 0.99768 0.06716
17:17 68_ Форма 10. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.42499 0.87165 0.24413
17:17 68_ Форма 11. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.03780 -0.57782 -0.81529
17:17 68_ Форма 12. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.26546 0.93464 -0.23661
17:17 68_ Форма 13. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.21240 0.96610 -0.14672
17:17 68_ Форма 14. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.31265 -0.52968 0.78847
17:17 68_ Форма 15. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.09669 -0.69410 0.71336
17:17 68_ Форма 16. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.09700 0.90146 0.42185
17:17 68_ Форма 17. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.08046 -0.99474 -0.06346
17:17 68_ Форма 18. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.51134 0.85633 0.07232
17:17 68_ Форма 19. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.76308 0.56145 -0.32014
17:17 68_ Форма 20. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.65648 -0.75166 0.06357
17:17 68_ Форма 21. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.35034 0.92396 -0.15347
17:17 68_ Форма 22. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.17221 0.97932 -0.10615
17:17 68_ Форма 23. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.92399 -0.37716 0.06322
17:17 68_ Форма 24. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
-0.99850 0.05100 0.01985
17:17 68_ Форма 25. Направляющие косинусы поступательного движения
из условия максимума динамической реакции
0.05129 -0.98883 0.13993
17:17 502_ Накопление нагрузок основной схемы.
17:17 37_ Суммарные узловые нагрузки на основную схему
X Y Z UX UY UZ
1- 0.0 0.0 4.468+3 -5.370-2 -1.908-2 -3.696-7
2- 0.0 0.0 1.604+3 -4.408-2 -1.152-2 0.0
3- 0.0 0.0 7.021+1 -2.302-3 -1.978-3 0.0
4- 8.940 0.0 0.0 0.0 0.0 0.0
5- 0.0 -2.468+1 0.0 0.0 0.0 0.0
6- 1 1.261+1 -4.295+1 -1.342-1 -4.489-2 -1.624-2 5.306-5
6- 2 1.459+2 4.229+1 5.167-1 4.759-2 -1.866-1 1.664-3
6- 7 4.241+1 2.238 4.903-1 4.234-3 4.311-2 -1.684-3
6- 23 7.384 3.014 -5.052-1 -2.320-3 -3.562-2 1.625-4
7- 1 -4.295+1 1.463+2 4.574-1 1.529-1 5.535-2 -1.808-4
7- 2 4.229+1 1.226+1 1.498-1 1.379-2 -5.410-2 4.823-4
7- 3 3.482 4.994 -2.662-1 3.123-3 -3.075-3 -2.105-3
7- 9 5.235-1 4.786+1 3.222 -9.047-2 1.523-2 -1.712-4
7- 17 4.913-1 6.075 3.876-1 -3.795-3 -3.744-3 -1.794-3
7- 18 2.605 4.363 3.684-1 -5.439-3 -3.231-3 -3.970-4
7- 21 1.576 4.156 -6.902-1 -6.562-3 -3.521-3 -1.890-4
7- 22 -5.493 3.124+1 -3.386 -5.543-2 3.586-2 -4.188-3
17:17 580_ Вычисление перемещений в основной схеме.
17:17 268_ Загружение. Работа внешних сил
1 1.633+1
2 2.432
3 9.203-3
4 1.039-3
5 1.070-2
6- 1 4.977-2
6- 2 4.557-1
6- 7 9.856-3
6- 23 5.535-4
7- 1 5.778-1
7- 2 3.829-2
7- 3 8.523-3
7- 9 8.780-3
7- 17 5.760-4
7- 18 3.943-4
7- 21 3.319-4
7- 22 2.484-3
17:17 586_ Вычисление усилий в основной схеме.
17:17 604_ Выбор расчетных сочетаний усилий в основной схеме.
17:17 7_ ЗАДАНИЕ ВЫПОЛНЕНО. Время расчета 5.17 мин.
Таблица 5.10 – Частоты собственных колебаний
|
№ загр |
№ формы |
Собст. значения |
Частоты |
Период (с) |
Коэф. распред. |
Мод. масса (%) |
Сумма мод.масс (%) | |
|
Круг.частота (рад/с) |
Частота (Гц) | |||||||
|
6 |
1 |
0.126 |
7.949 |
1.265 |
0.790 |
-5.026 |
4.642 |
4.642 |
|
6 |
2 |
0.108 |
9.293 |
1.479 |
0.676 |
16.444 |
49.693 |
54.335 |
|
6 |
3 |
0.072 |
13.905 |
2.213 |
0.452 |
1.918 |
0.676 |
55.011 |
|
6 |
4 |
0.031 |
32.077 |
5.105 |
0.196 |
-0.007 |
0.000 |
55.011 |
|
6 |
5 |
0.029 |
34.365 |
5.469 |
0.183 |
-1.198 |
0.264 |
55.275 |
|
6 |
6 |
0.027 |
36.881 |
5.870 |
0.170 |
1.104 |
0.224 |
55.499 |
|
6 |
7 |
0.026 |
38.847 |
6.183 |
0.162 |
7.776 |
11.111 |
66.609 |
|
6 |
8 |
0.024 |
41.277 |
6.569 |
0.152 |
-0.763 |
0.107 |
66.716 |
|
6 |
9 |
0.023 |
43.720 |
6.958 |
0.144 |
0.090 |
0.002 |
66.718 |
|
6 |
10 |
0.021 |
47.207 |
7.513 |
0.133 |
0.155 |
0.004 |
66.722 |
|
6 |
11 |
0.021 |
47.798 |
7.607 |
0.131 |
-0.078 |
0.001 |
66.723 |
|
6 |
12 |
0.019 |
51.703 |
8.229 |
0.122 |
-0.455 |
0.038 |
66.761 |
|
6 |
13 |
0.018 |
55.588 |
8.847 |
0.113 |
-0.174 |
0.006 |
66.767 |
|
6 |
14 |
0.018 |
56.587 |
9.006 |
0.111 |
0.184 |
0.006 |
66.773 |
|
6 |
15 |
0.017 |
57.611 |
9.169 |
0.109 |
0.052 |
0.000 |
66.774 |
|
6 |
16 |
0.017 |
59.741 |
9.508 |
0.105 |
-0.034 |
0.000 |
66.774 |
|
6 |
17 |
0.016 |
60.819 |
9.680 |
0.103 |
-0.238 |
0.010 |
66.784 |
|
6 |
18 |
0.016 |
62.289 |
9.914 |
0.101 |
1.489 |
0.408 |
67.192 |
|
6 |
19 |
0.016 |
62.838 |
10.001 |
0.100 |
-0.721 |
0.095 |
67.287 |
|
6 |
20 |
0.016 |
64.422 |
10.253 |
0.098 |
-1.959 |
0.705 |
67.993 |
|
6 |
21 |
0.015 |
65.463 |
10.419 |
0.096 |
0.934 |
0.160 |
68.153 |
|
6 |
22 |
0.015 |
65.568 |
10.435 |
0.096 |
-1.188 |
0.260 |
68.413 |
|
6 |
23 |
0.015 |
67.089 |
10.677 |
0.094 |
-3.308 |
2.011 |
70.424 |
|
6 |
24 |
0.015 |
67.235 |
10.701 |
0.093 |
-1.040 |
0.199 |
70.622 |
|
6 |
25 |
0.015 |
67.434 |
10.733 |
0.093 |
0.097 |
0.002 |
70.624 |
|
7 |
1 |
0.126 |
7.949 |
1.265 |
0.790 |
17.126 |
53.895 |
53.895 |
|
7 |
2 |
0.108 |
9.293 |
1.479 |
0.676 |
4.767 |
4.176 |
58.071 |
|
7 |
3 |
0.072 |
13.905 |
2.213 |
0.452 |
2.751 |
1.391 |
59.461 |
|
7 |
4 |
0.031 |
32.077 |
5.105 |
0.196 |
-0.241 |
0.011 |
59.472 |
|
7 |
5 |
0.029 |
34.365 |
5.469 |
0.183 |
0.425 |
0.033 |
59.505 |
|
7 |
6 |
0.027 |
36.881 |
5.870 |
0.170 |
-1.058 |
0.206 |
59.711 |
|
7 |
7 |
0.026 |
38.847 |
6.183 |
0.162 |
0.410 |
0.031 |
59.742 |
|
7 |
8 |
0.024 |
41.277 |
6.569 |
0.152 |
0.083 |
0.001 |
59.743 |
|
7 |
9 |
0.023 |
43.720 |
6.958 |
0.144 |
8.260 |
12.538 |
72.281 |
|
7 |
10 |
0.021 |
47.207 |
7.513 |
0.133 |
0.318 |
0.019 |
72.300 |
|
7 |
11 |
0.021 |
47.798 |
7.607 |
0.131 |
-1.199 |
0.264 |
72.564 |
|
7 |
12 |
0.019 |
51.703 |
8.229 |
0.122 |
1.602 |
0.471 |
73.035 |
|
7 |
13 |
0.018 |
55.588 |
8.847 |
0.113 |
0.793 |
0.115 |
73.151 |
|
7 |
14 |
0.018 |
56.587 |
9.006 |
0.111 |
-0.312 |
0.018 |
73.168 |
|
7 |
15 |
0.017 |
57.611 |
9.169 |
0.109 |
-0.371 |
0.025 |
73.194 |
|
7 |
16 |
0.017 |
59.741 |
9.508 |
0.105 |
0.317 |
0.018 |
73.212 |
|
7 |
17 |
0.016 |
60.819 |
9.680 |
0.103 |
-2.943 |
1.592 |
74.804 |
|
7 |
18 |
0.016 |
62.289 |
9.914 |
0.101 |
2.494 |
1.143 |
75.947 |
|
7 |
19 |
0.016 |
62.838 |
10.001 |
0.100 |
0.530 |
0.052 |
75.998 |
|
7 |
20 |
0.016 |
64.422 |
10.253 |
0.098 |
-2.243 |
0.925 |
76.923 |
|
7 |
21 |
0.015 |
65.463 |
10.419 |
0.096 |
2.464 |
1.116 |
78.039 |
|
7 |
22 |
0.015 |
65.568 |
10.435 |
0.096 |
6.759 |
8.394 |
86.433 |
|
7 |
23 |
0.015 |
67.089 |
10.677 |
0.094 |
-1.350 |
0.335 |
86.768 |
|
7 |
24 |
0.015 |
67.235 |
10.701 |
0.093 |
0.053 |
0.001 |
86.769 |
|
7 |
25 |
0.015 |
67.434 |
10.733 |
0.093 |
-1.864 |
0.638 |
87.407 |
Наиболее весомая модальная масса в загружении 6 имеют 1-я, 2-я, 7-я, 23-я формы колебаний, а для загружения 7 – 1-я, 2-я, 3-я, 9-я, 17-я, 18-я, 21-я и 22-я формы. По каждому динамическому загружению превышен минимальный процент учета суммы модальных масс (не менее 70%). Для 6-го загружения сумма модальных масс составляет 70,62 %, для 7-го – 87,41 %.
|
|
|
Рис. 5.13 – Загружение 6; 1-я и 2-я формы колебаний
|
|
|
Рис. 5.14 – Загружение 6; 7-я и 23-я формы колебаний
|
|
|
Рис. 5.15 – Загружение 7; 1-я и 2-я формы колебаний
|
|
|
Рис. 5.16 – Загружение 7; 3-я и 9-я формы колебаний
|
|
|
Рис. 5.17 – Загружение 7; 17-я и 18-я формы колебаний
|
|
|
Рис. 5.18 – Загружение 7; 21-я и 22-я формы колебаний
Результаты расчета каркаса в графическом виде приведены на
рис. 5.19 5.33. Наиболее опасным является особые сочетания нагрузок.

Рис. 5.19 – Фундаментная плита. Изополя Мх. 7 сочетание

Рис. 5.20 – Фундаментная плита. Изополя Мy. 7 сочетание

Рис. 5.21 – Фундаментная плита. Изополя Qx. 7 сочетание
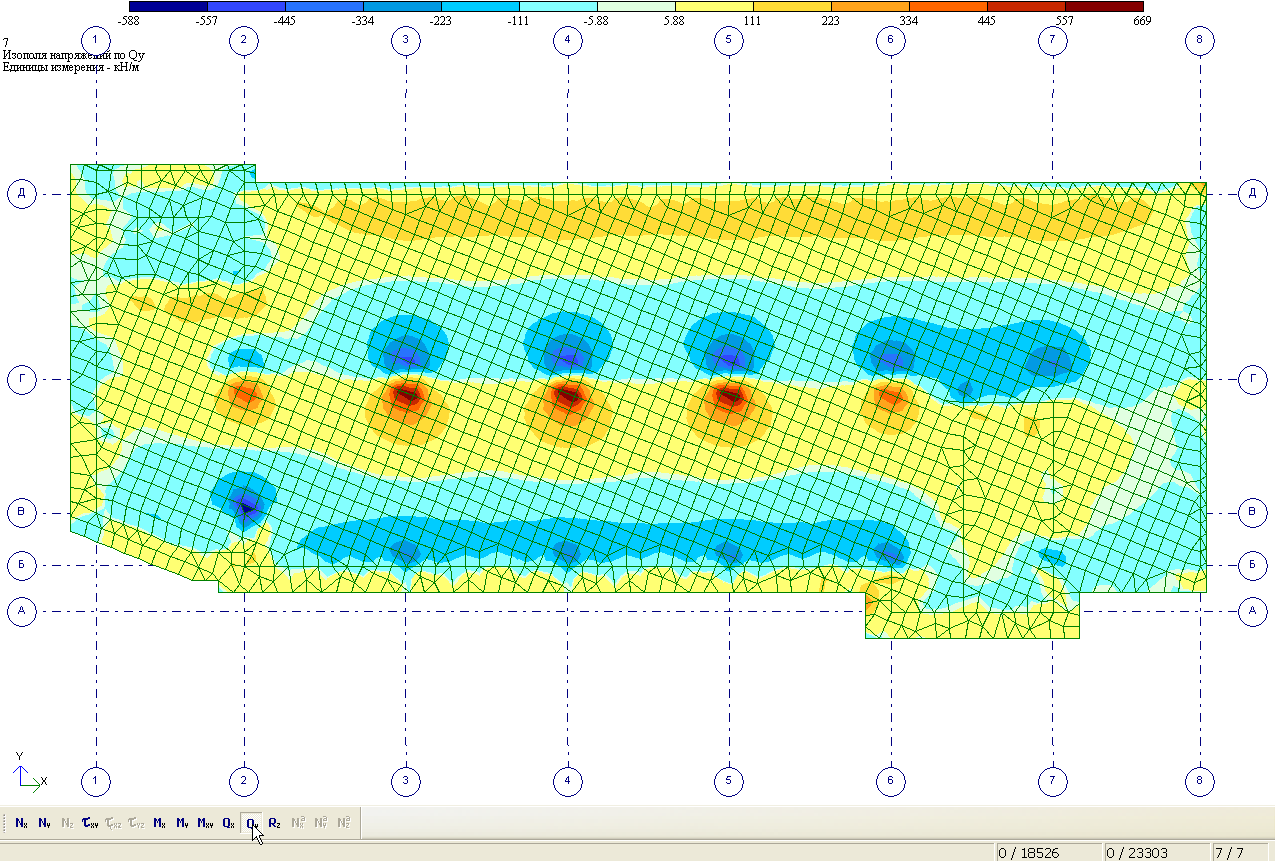
Рис. 5.22 – Фундаментная плита. Изополя Qy. 7 сочетание

Рис. 5.23 – Колонны. Мозайка N. 7 сочетание
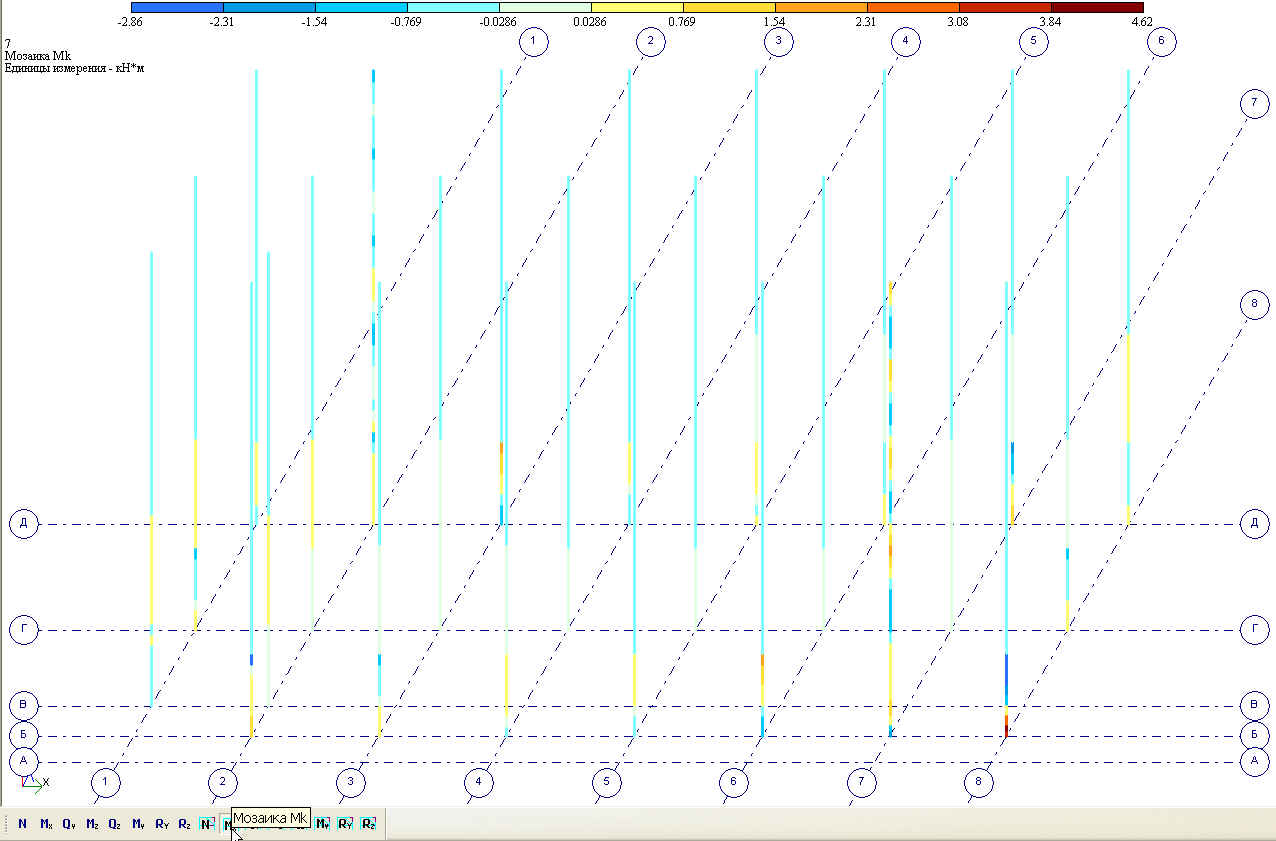
Рис. 5.24 – Колонны. Крутящий момент Мk. 7 сочетание

Рис. 5.25 – Колонны. Изгибающий момент Мz. 7 сочетание

Рис. 5.26 – Колонны. Изгибающий момент Му. 7 сочетание