Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Кубанский государственный технологический университет»

Кафедра электроснабжения промышленных предприятий

Составление структурных схем и анализ статической устойчивости системы

Р у к о в о д с т в о

к лабораторной работе № 5

по курсу «Математическое моделирование в электроэнергетике»

для студентов всех форм обучения направления

140400.62 – «Электроэнергетика и электротехника»

Краснодар 2013

Составитель: канд. техн. наук, доц. Е.А. Беседин

УДК 621.316.001

СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ И АНАЛИЗ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ: Руководство к лабораторной работе № 5 по курсу «Математическое моделирование в электроэнергетике» для студентов всех форм обучения направления 140400.62 – «Электроэнергетика и электротехника» / Кубан. гос. технол. ун-т; Сост. Е.А. Беседин. Краснодар, 2013. – 33 с.

Рассматриваются основные элементарные звенья и передаточные функции. Приведены примеры преобразования структурных схем. Даны варианты заданий к лабораторной работе.

Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.

Рецензенты: канд. техн. наук, доц. А.М. Смаглиев

(кафедра ЭПП КубГТУ),

д-р техн. наук, проф. А.Н. Плахотнюк

(кафедра электротехники, КубГТУ)

1 Общие сведения

1.1. Основные положения

Основой для получения дифференциальных уравнений служит знание физических закономерностей протекания процессов в различ­ных элементах системы. Однако таких элементов может быть много и связи между ними могут быть различными. Поэтому часто прибегают к структурному изображению системы, на котором схематиче­ски показывают различные ее элементы (звенья) и связь между ними. Такое изображение системы, где в отличие от схемы замещения вни­мание обращено на взаимную связь элементов, а не на их содержа­ние, называется структурной схемой системы.

Структурные схемы позволяют более наглядно изучить влияние взаимодействия элементов системы на ее устойчивость и переходные процессы. Одновременно они выявляют ряд общих черт в задачах, которые при непосредственном описании в виде дифференциальных уравнений были бы незаметны, а также позволяют установить некоторые общие закономерности.

Структурная схема называется разомкнутой, если цепь прохо­ждения сигналов разомкнута, т.е. выходная величина не связана с входной, или, как говорят, нет обратной связи. Для регулируемых систем они всегда замкнуты и, как правило, являются сложными. Эти схемы могут быть составлены либо на основании записанной системы дифференциальных уравнений, либо на основании сведений о функциях отдельных элементов системы и взаимной связи между ними. Данные схемы широко применяются для изучения процессов в системах автоматического регулирования.

Основной частью структурной схемы является некоторый объект, который имеет некоторые свои особенности (рисунок 1.1)

Рисунок 1.1 – Основная часть структурной схемы

Здесь - входной сигнал объекта, а- выходной сигнал или реакция объекта. Объект представляет собой совокупность звеньев, которые соединяются между собой с помощью связей таким образом, чтобы реальный объект представить в виде определенной совокупности типовых звеньев. Соотношение выходного и входного сигналов объекта, выраженное в операторной форме, называетсяпередаточной функцией объекта

(1.1)

Аналогично определяются передаточные функции и отдельных типовых звеньев, входящих в структурную схему. Зная передаточные функции отдельных звеньев, можно определить расчетным путем и передаточную функцию сложной системы в целом.

1.2. Элементарные звенья и их передаточные функции

Наиболее характерными звеньями регулируемой электрической системы, как и большинства регулируемых систем, являются: усилительное (безынерционное), инерционное (апериодическое), дифференцирующее, интегрирующее, запаздывающее, колебательное, суммирующее. Каждое звено харак­теризуется своей передаточной функцией, связывающей изображения входной и выходной величин, которая полностью опре­деляет динамические свойства звена. Рассмотрим передаточ­ные функции элементарных звеньев.

1. Усилительное (безынерционное или пропорциональное) звено (риунок 1.2 а) является самым простым звеном, выходная величина которого прямо пропорциональна входной.

а б

Рисунок 1.2 – Пропорциональное звено

Уравнение такого звена

, (1.2)

где - коэффициент усиления, может быть как размерным, так и безразмерным.

Передаточная функция звена

. (1.3)

Примером такого звена является делитель на­пряжения (рисунок 1.2 б).

Инерционное (апериодическое) звено(рис. 1.3 а) одно из са­мых распространенных в автоматически регулируемых системах, описывается дифференциальным уравнением

, (1.4)

где - постоянная времени;

- коэффициент усиления.

а б в

Рисунок 1.3 – Инерционное (апериодическое) звено

Передаточная функция этого звена имеет вид

. (1.5)

В установившемся режиме инерционное звено имеет те же пара­метры, что и усилительное. Примерами такого звена (рисунок 1.3 б, в) являются четырехполюсники, содержащие индуктивность или емкость.

Дифференцирующее звено (рисунок 1.4 а), называемое иногда реальным, определяется дифференциальным уравнением

, (1.6)

а б в

Рисунок 1.4 – Дифференцирующее звено

Передаточная функция такого звена

. (1.7)

Установившееся значение выходной величины равно нулю. Дифференцирующее звено с (при) имеет передаточную функцию

. (1.8)

и называется идеальным дифференцирующим звеном.

Примерами такого звена (рисунок 1.4 б, в) являются четырехполюсники, содержащие соответствующим образом включенные активные и реактивные сопротивления.

Интегрирующее звено(рисунок 1.5 а) определяется уравнением

, (1.9)

т.е. входная величина пропорциональна интегралу от входной

а б в

Рисунок 1.5 – Интегрирующее звено

Передаточная функция этого звена равна

. (1.10)

Примерами такого звена являются электрическая индуктивность и емкость (рисунок 1.5 б, в).

Запаздывающее звеноопределяется уравнением

. (1.11)

Передаточная функция такого звена имеет вид

. (1.12)

Примерами такого звена являются различные схемные решения линий задержки.

Колебательное звено(рисунок 1.6 а) описывается дифференциальным уравнением второго порядка

, (1.13)

где - коэффициент демпфирования;

- коэффициенты усиления;

- входной и выходной сигналы.

Разделим уравнение (1.13) на , получим

, (1.14)

где - коэффициент затухания,

; (1.15)

- собственная частота колебаний звена (без демпфирования)

. (1.16)

а б

Рисунок 1.6 – Колебательное звено

В операторной форме уравнение (1.14) запишется в виде

, (1.17)

откуда

, (1.18)

Колебательное звено является важнейшим элементом структурных схем при изучении электромеханических переходных процессов в электрических системах. Примером такого звена может служить электрический колебательный контур, приведенный на рисунке 1.6 б. Здесь

;;.

Суммирующее звено с выходной величиной и входными величинами, где

. (1.19)

На схемах суммирующее звено изображают либо в виде кружка (рисунок 1.7 а), либо в виде вертикальной черты (рисунок 1.7 б), к которым, с одной стороны, подходят входные величины , а с другой стороны, отходит выходная величина.

а б

Рисунок 1.7 – Суммирующее звено

1.3. Передаточная функция системы элементарных звеньев

Передаточная функция разомкнутой цепи зави­сит от вида соединений звеньев.

Последовательнымсоединением звеньев называется такое, при ко­тором выходная величина предшествующего звена является входной величиной последующего звена (рисунок 1.8)

Рисунок 1.8 – Последовательное соединение элементарных звеньев

Эту схему можно описать следующей системой уравнений

. (1.20)

Подставим в последнее уравнение значение из предпоследнего уравнения. В полученное уравнение подставим значенийиз следующего уравнения, и т.д. В результате получим

, (1.21)

откуда

. (1.22)

Следовательно, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.

Параллельнымсоединением звеньев называется такое, при котором входной величиной всех звеньев является одна и та же величина, а выходные величины суммируются (рисунок 1.9)

Рисунок 1.9 – Параллельное соединение элементарных звеньев

Эту схему можно описать следующей системой уравнений

. (1.23)

По определению данной схемы . С учетом этого и на основании системы уравнений (1.23) получим

. (1.24)

Следовательно, передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев.

На практике структурные схемы представляют собой совокупность последовательного и параллельного соединения звеньев, т.е. представляют собой схемы смешанного вида. Для них составляют сложное выражение передаточной функции системы, используя соотношения (1.22) и (1.24). Затем выражение приводится к общему знаменателю и производится приведение подобных членов. В результате передаточная функция разомкнутой системы, представляющей собой совокупность последовательно и параллельно соединенных звеньев, будет представлять собой соотношение двух многочленов

. (1.25)

В большинстве случаев степень многочлена числителя меньше степени многочленазнаменателя. Уравнениеявляется характеристическим уравнением разомкнутой системы.

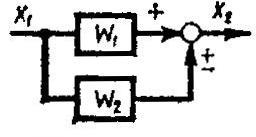
1.4. Структурные схемы с обратной связью

Для изменения статических и динами­ческих характеристик системы вводятся обратные связи. Эти изменения зависят от способа соединения и типа звеньев, включенных в цепь обратной связи.

Пусть некоторое звено с передаточной функцией охвачено обратной связью, т.е. к выходу этого звена присоединяется второе звено с передаточной функцией, выход которого подается на вход первого звена с положительным знаком (положительная обратная связь) или с отрицательным знаком (отрицательная обратная связь) (рисунок 1.10)

Рисунок 1.10 – Структурная схема с обратной связью

Найдем передаточную функцию эквивалентного звена, полученного из первого звена, охваченного обратной связью с помощью второго звена. Вход эквивалентного звена обозначим через, выход –. Чтобы полу­чить функцию, в которой

, (1.26)

запишем соотношения между переменными на входе и выходе отдель­ных звеньев:

. (1.27)

где знак «+» соответствует положительной обратной связи, а знак «–» - отрицательной.

Учитывая эти соотношения, последовательно получим:

;

;

, (1.28)

откуда

, (1.29)

где знак «–» соответствует положительной обратной связи, а знак «+» - отрицательной.

Часто в системах автоматического регулирования охватывают обратной связью инерционное зве­но, чтобы получить новое эквивалент­ное инерционное звено с измененными параметрами. В качестве об­ратной связи применяют либо безынерционное звено – такая обратная связь называется жесткой, либо дифференцирующее звено – такая обратная связь называется гибкой.

Рассмотрим инерционное звено, охваченное жесткой обратной связью. Передаточная функция звена с отрицательной обратной связью имеет вид

. (1.30)

Найдем передаточную функцию эквивалентного звена с помощью выражения (1.29)

, (1.31)

где - коэффициент усиления эквивалентного инерционного звена, равный

; (1.32)

- постоянная времени эквивалентного инерционного звена

. (1.33)

Таким образом, при охвате инерционного звена жесткой обратной связью получа­ется новое инерционное звено с уменьшенными коэффициентом уси­ления и постоянной времени. Отношение коэффициента усиления к постоянной времени остается неизменным. В системах автоматиче­ского регулирования возбуждения (АРВ сильного действия) синхрон­ных машин часто возбудитель охватывают такой связью для уменьшения его постоянной времени.

В некоторых случаях инерционное звено охватывают жесткой обратной связью с коэффициентом усиления . Тогда согласно (1.32)

, (1.34)

т.е. коэффициент усиления системы определяется обратной величи­ной коэффициента усиления элемента обратной связи.

Теперь рассмотрим инерционное звено, охваченное гибкой отрица­тельной обратной связью. Передаточная функция звена об­ратной связи в этом случае имеет вид

, (1.35)

Часто параметры звена обратной связи выбирают такими, чтобы , т.е. применяют идеальное дифференцирующее звено с передаточной функцией . Для такой обратной связи найдем передаточную функцию эквивалентного звена с помощью выражения (1.29)

, (1.36)

где

. (1.37)

Таким образом, при охвате инерционного звена гибкой обратной связью получа­ется новое инерционное звено с неизменным коэффициентом усиле­ния и увеличенной постоянной времени. Гибкая отрицательная обратная связь не меняет статические характеристики инерционного звена, меняя его динамические характеристики.

1.5. Преобразования структурных схем

Структурная схема реальной системы, как правило, оказывается сложной, многоконтурной, что обусловлено наличием нескольких цепей обратных связей и несколь­ких точек приложения внешних сил. Любую многоконтурную сис­тему можно свести к одноконтурной системе либо с единичной об­ратной связью (чтобы записать передаточную функцию разомкнутой системы), либо со звеном обратной связи (чтобы исследовать его влияние на характеристику системы).

Для сравнения влияния внешних сил, приложенных в разных точках системы, часто целесообразно преобразовать структурную схему, выделив эквивалентные входные сигналы. Преобразование структурных схем производится на основании правил, изложенных выше. Однако можно привести некоторые дополнительные правила, которые в ряде случаев облегчают преобразования. Так, в пп. 1 и 2 приведенной ниже таблицы 1.1 даны преобразования, устраняющие одно звено из цепи обрат­ной связи (для получения эквивалентной схемы, содержащей еди­ничную обратную связь) или из прямой цепи. Эквивалентная схема получается при соответствующем приравнивании вход­ных и выходных величин первоначальной схемы.

Таблица 1.1 – Правила преобразования структурных схем

Номер п/п	Вид преобразования	Исходная Схема	Эквивалентная Схема	Уравнение
1.	Устранение звена из цепи обратной связи
2.	Устранение параллельного звена в прямой цепи
3.	Перемещение точки присоединения на вход звена
4.	Перемещение точки присоединения на выход звена
5.	Перемещение суммирующей точки на вход звена

Продолжение таблицы 1.1

Номер п/п	Вид преобразования	Исходная Схема	Эквивалентная Схема	Уравнение
6.	Перемещение суммирующей точки на выход звена

1.6. Пример преобразования структурной схемы

Необходимо получить переда­точную функцию разомкнутой си­стемы, упростив сложную структур­ную схему, приведенную на рисунке 1.11, с двумя «перекрещивающимися» обратными связями, имеющими передаточные функции и.

Рисунок 1.11 – Исходная структурная схема

Применим правило, изложенное в п. 3 таблицы 1.1, к точке входа звена . Получим новую схему (рисунок 1.12 а), из которой очевидно, что звено с оператором, охваченное отрицатель­ной обратной связью, состоящей из двух последовательно соеди­ненных звеньеви, можно заменить одним звеном с передаточной функцией:

.

Соответствующая упрощенная схема приведена на рисунке 1.12 б. Ее можно еще упро­стить, заменив последовательное соединение звеньев с передаточ­ными функциями и, охваченных отрицательной обрат­ной связью – звеном, од­ним звеном с передаточной функ­цией

.

Рисунок 1.12 – Этапы преобразования структурной схемы

Очередная схема приведена на рисунке 1.12 в. Последовательно соединенные звенья в прямой цепи этой схемы можно заменить (рисунок 1.12 г) звеном, передаточная функция которого представляет собой передаточную функ­цию разомкнутой системы исходной структурной схемы

.

1.7. Частотные характеристики системы

Если на вход линейной устойчивой системы длительно действует гармонически изменяющаяся сила, то после затухания переходных процессов на выходе установятся гармонические колебания с такой же частотой (рисунок 1.13). Однако амплитуда и начальная фаза их будут зависеть от динамических свойств системы. Запишем уравнение, связывающее входные и выходные величины:

. (1.38)

Рисунок 1.13 – Входной и выходной гармонические сигналы

Гармоническим сигналом называется сигнал вида

(1.39)

или в комплексной форме

. (1.40)

Частным случаем такого сигнала являются сигналы

; (1.41)

. (1.42)

Выражение (1.41) соответствует случаю, когда , а выражение (1.42) – случаю, когда.

Пусть входной сигнал имеет фиксированную частоту. На комплексной плоскости этот сигнал изобразится в виде вектора с амплитудой , вращающегося против часовой стрелки вокруг начала координат с частотой. Тогда на выходе получим гармонический сигнал. Для удобства рассмотрения пусть прифаза входного сигнала. Выходной сигнал тогда может быть представлен на комплексной плоскости в виде вектора с амплитудой, сдвинутого на уголотносительно вектора входного сигнала, и вращающегося относительно начала координат с той же частотой

. (1.43)

Подставим выражения (1.39) и (1.43) в выражение (1.38) при , получим

. (1.44)

откуда

(1.45)

Функция (1.45) называется комплексным коэффициентом усиле­ния (при частоте ). Формально комплексный коэффициент усиле­ния получается из передаточной функциипри подстановкеи является отношением выходного гармонического сигнала к входному гармоническому сигналу.

В вышеприведенных выражениях и- функции частоты при неизменной амплитудевходного сигнала. Каждой фиксированной частоте входного гармонического сигнала будут соответствовать определенные значения амплитуды выходного сигнала и сдвига фазы.

Комплексную функцию действи­тельного переменногоможно представить в виде

, (1.46)

где

. (1.47)

При каждом фиксированном со значение однозначно определяет (рисунок 1.14) точку на комплексной плоскости с декарто­выми координатами,или поляр­ными координатами,.

Рисунок 1.14 – Графическое представление функции

Следователь­но, можно записать формулы перехода от полярных координат к декартовым, и наоборот:

. (1.48)

Зависимости ,,,(рисунок 1.15, а – г) назы­ваются частотными характеристиками системы – амплитудной, фа­зовой, вещественной и мнимой соответственно.

Рисунок 1.15 – Частотные характеристики системы

Вектор-годограф , построенный на комплексной плоскости (рисунок 1.16) при изменении частоты отдо, называется амплитудно-фазовой частотной характеристикой системы.

Комплексный коэффициент усиления и частотные характеристики являются важными характеристиками звена и системы, позволяющими исследовать устойчивость и характер протекания пере­ходных процессов. Зная величину , можно определить реак­цию линейной системы не только на синусоидальный входной сигнал, но и на любую другую внешнюю силу, представленную в виде интеграла Фурье, т.е. в виде бесконечной суммы синусоидальных колебаний всех частот. Зная, как про­ходит каждое из этих колебаний через систему, и складывая их на выходе, мож­но получить значение выходной величи­ны.

Рисунок 1.16 – Амплитудно-фазовая частотная характеристика

Частотные характеристики элементов системы и всей системы могут быть по­лучены экспериментально с помощью гене­ратора синусоидальных колебаний и соот­ветствующей измерительной аппаратуры для измерения частоты, амплитуды и фазы колебаний. Полученные эксперименталь­ные частотные характеристики являются одной из форм задания математической модели системы, которая может непосредственно использоваться в расчетах устойчивости и пере­ходных процессов.

1.8. Анализ устойчивости систем автоматического регулирования

Устойчивость – это способность системы возвращаться в исходное или близкое к исходному состояние после малого возмущения.

Свойство, обратное устойчивости, называется неустойчивостью.

Устойчивость состояния равновесия является необходимым условием работоспособности системы. В противном случае малые начальные отклонения, которые всегда имеют место в реаль­ных условиях, будут вызывать нарастающие со временем отклоне­ния и, как следствие, недопустимое изменение условий работы системы.

Существуют необходимые и достаточные условия устойчивости. Условие устойчивости называется необходимым, если при невы­полнении его появляется неустойчивость. Условие устойчивости называется достаточным, если при его выполнении имеет место устойчивость. Условие устойчивости необходимое, но недостаточное, означает, что его выполнения недостаточно для того, чтобы имела место устойчивость: может появиться как устойчивость, так и не­устойчивость. Вопрос об устойчивости должен в этом случае решаться дополнительными исследованиями.

Необходимое и достаточное условие статической устойчивости обеспечивается тогда и только тогда, когда все корни характери­стического уравнения этой системы

(1.49)

имеют отрицательные вещественные части.

Так как коэффициенты уравнения (1.49), определяемые реальными параметрами технической системы, всегда действительны, то его корни могут быть действительными и комплексно-сопряженными.

Рассматривая корни характеристического уравнения как точки комплексной плоскости (рисунок 1.17)

, (1.50)

приведенное условие можно сформулировать и так: для того чтобы состояние равновесия было асимптотически устойчиво, необ­ходимо и достаточно, чтобы все корни характери­стического уравнения (1.49) лежали в левой полуплоскости корней.

Рисунок 1.17 – Корни характеристического уравнения на комплексной плоскости

Характеристическое уравнение электрической системы обычно содержит несколько действительных корней и несколько комплексно-сопряженных.

Выходной сигнал можно описать следующим выражением на основании решения характеристического уравнения системы

. (1.51)

При этом для действительных корней решение имеет вид , а для пары комплексных корней -. В зависимости от того, какие корни имеет решение характеристического уравнения, можно установить не только устойчивость или неустойчивость системы, но также и определить функции, составляющие переходный процесс.

1. Если решение содержит только действительные корни и для всех корней, то процесс апериодически затухает (рисунок 1.18).

Рисунок 1.18 – Апериодический затухающий процесс

2. Если решение содержит только действительные корни и хотя бы для одного корня , то составляющая, соответствующая этому корню, неограниченно возрастает во времени (рисунок 1.19). Система будет неустойчивой. При этом говорят, что происходит апериодическое нарушение устойчивости.

Рисунок 1.19 – Апериодическое нарушение устойчивости

3. Если решение содержит действительные и комплексные корни, при этом ,для всех корней, то имеем колебательный процесс, амплитуда которого апериодически затухает (рисунок 1.20).

Рисунок 1.20 – Колебательный затухающий процесс

4. Если решение содержит действительные и комплексные корни, при этом хотя бы одна пара (остальные корни левые), то имеем колебательный процесс, амплитуда которого апериодически нарастает (рисунок 1.21). Система неустойчива, при этом говорят, что происходит колебательное нарушение устойчивости или самораскачивание.

Рисунок 1.21 – Колебательное нарушение устойчивости

Если система оказывается неустойчивой, инженеру важно еще знать, как происходит нарушение устойчивости. Зная характер нарушения устойчивости, иногда из чисто физических соображений можно наметить мероприятия, устраняющие нарушение устойчивости. Поэтому в процессе решения задачи устойчивости желательно полу­чить представление и о характере нарушения устойчивости.

Выявление возможной неустойчивости и определение хода про­цессов при нарушении может быть проведено путем отыскания корней характеристического уравнения. Однако при высокой степени уравнения задача отыскания его корней оказывается весьма трудоемкой. Далее излагается ряд наиболее распространенных критериев и методов изучения устойчивости.

1.9. Алгебраические критерии устойчивости

Алгебраические критерии устойчивости основаны на закономерностях, связывающих отрица­тельность всех действительных частей корней уравнения (1.49) со знаками коэффициентов этого уравнения и некоторых функций от коэффициентов. Алгебраические критерии содержат группу усло­вий, при соблюдении которых имеет место устойчивость. Если же хотя бы одно из них нарушено, то имеет место неустойчивость. Для проведения анализа устойчивости с помощью алгебраических критериев необходимо предварительно вычислить коэффициенты характеристического уравнения

.

Необходимое условие устойчивости – если состояние равновесия системы (1.49) асимптотически устойчиво, то все коэффициенты положительны:

. (1.52)

Данное условие является необходимым и достаточным для отсутствия апериодической неустойчивости. Если при изменении параметров система становится неустойчивой, а все коэффициенты характеристического уравнения положительны, то неустойчивость имеет характер самораскачивания.

Для устой­чивости системы требуется, чтобы коэффициенты характеристического многочлена не только были положительными, но и удовлет­воряли некоторым соотношениям. Критерий Гурвица устанавливает эти соотношения в форме неравенств, соблюдение которых является необходимым и достаточ­ным условием устойчивости системы любого порядка.

Система неравенств Гурвица строится следующим образом. Из коэффициентов характеристического многочлена -й степени вида (1.49) составляется квадратная матрица Гурвица-го порядка

. (1.53)

Правило составления матрицы Гурвица следующее. По главной диагонали располагают коэффициенты многочлена (1.49) в порядке их нумерации, начиная с до. В строках помещают поочередно коэффициенты только с нечетными или только с чет­ными индексами (включая и коэффициент), причем влево от диагонали с уменьшающимися, вправо — с увеличивающимися ин­дексами. Все недостающие коэффициенты, т.е. коэффициенты с ин­дексами меньше нуля или больше, заменяют нулями. Для соблю­дения устойчивости требуется, чтобы вседиагональных минора матрицы (1.53) были положительными. Диагональные миноры (назы­ваемые определителями Гурвица) получаются отчеркиванием их слева и сверху, как показано в матрице (1.53). Первый минор состоит из коэффициента. Последний минор включает в себя матрицу Гурвица целиком.

Например, характеристическое уравнение имеет вид:

.

Матрица Гурвица имеет вид:

.

Найдем ее определители

;

.

Система неустойчива, дальше можно не вычислять.

Критерий Гурвица используется для характеристических уравнений невысокого порядка – третьего-четвертого. Для более задач высоких порядков используется алгебраический критерий Рауса с составлением специальной таблицы.

1.10. Частотные критерии

Пусть дано характеристическое уравнение вида (1.49). Подставим в это уравнение вместо, получим

. (1.54)

Возведем в соответствующие степени и затем представим данное уравнение в виде

. (1.55)

После преобразований получим

; (1.56)

. (1.57)

Вектор , изображенный в декартовых координатах на плос­кости, при измененииотдовращается и концом описывает кривую (рисунок 1.22), которая называется характеристичес­кой кривой или годографом характеристического уравнения

Рисунок 1.22 – Годограф характеристического уравнения

Критерий Михайлова имеет следую­щую формулировку: система будет устойчива тогда и только тогда, когда при возрастании отдовекторповернется на угол, где- степень характеристического уравнения, или, что то же самое, если при увеличенииотдогодограф, начинаясь на положительной части действительной оси, проходит последовательно в положительном направленииквадрантов.

Типичные годографы устойчивых систем для характерис­тических уравнений различных степенейот 1 до 5 приведены на рисунке 1.23. Характеристическая кривая устойчивой системы при из­мененииотдодолжна охватывать начало координат.

Рисунок 1.23 – Типичные годографы устойчивых систем