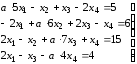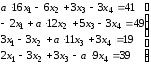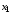Лабораторные / Лабораторные / LR2 / LR2

Министерство образования Российской Федерации

Кубанский государственный технологический университет

Кафедра электроснабжения промышленных предприятий

Лабораторная работа № 2

по курсу «Математическое моделирование в электроэнергетике»

ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Выполнил ст-т:

гр.11-НБ-ЭЭ1

Пелипенко С.П.

Проверил:

Беседин Е.А.

Краснодар 2013

1 ЦЕЛЬ И ПРОГРАММА РАБОТЫ

1.1 Целью работы является изучение использования основных численных алгоритмов в среде MathCadи MatLab для решения систем линейных и нелинейных уравнений.

1.2 В программу работы входит:

а) нахождение решения системы линейных уравнений методом обратной матрицы в среде MathCad;

б) нахождение решения системы линейных уравнений методом Гаусса путем ручных вычислений;

в) нахождение решения системы линейных уравнений методом Гаусса в средах MathCadи MatLab;

г) нахождение решения системы линейных уравнений итерационным методом простой итерации;

д) нахождение решения системы нелинейных уравнений итерационным методом Ньютона;

е) оформление отчета.

З А Д А Н И Е

к лабораторной работе № 2

1. В соответствии с вариантом задания найти решение системы линейных уравнений следующими методами:

1.1. Прямым методом обратной матрицы в среде MathCad.

1.2. Прямым методом Гаусса с обратным ходом путем проведения ручных расчетов.

1.3. Прямым методом Гаусса с обратным ходом в среде MathCad.

1.4. Прямым методом Гаусса с обратным ходом в среде MatLab.

1.5. Итерационным методом простой итерации в среде MathCad.

Вариант задания выбрать из таблицы П.1

Таблица П.1 – Варианты систем линейных уравнений

Номер варианта	Система линейных уравнений
1
2
3
4

Продолжение таблицы П.1

Номер варианта	Система линейных уравнений
5
6
7
8
9
10

Результаты расчета	Заданная точность приближения eps
	1,0	0,5	0,1	0,05	0,01	0,005	0,001	0,0005	0.00001

Примечание: номер варианта выбирается по последней цифре зачетной книжки. Для нулевой последней цифры выбирается вариант 10. Внутри уравнений в качестве значения принимается значение предпоследней цифры зачетной книжки. Если оно равно нулю, то значение .

2. В соответствии с вариантом задания найти решение системы нелинейных уравнений следующего вида методом Ньютона:

Примечание: внутри уравнений в качестве значения принимается значение предпоследней цифры зачетной книжки, а в качестве значения - значение последней цифры зачетной книжки. Если какое-либо значение из них равно нулю, то вместо нуля в уравнение подставляется 10.

Результаты расчета	Заданная точность приближения eps
	1,0	0,5	0,1	0,05	0,01	0,005	0,001	0,0005	0.00001

Выполнение работы:

Прямой метод обратной матрицы в среде MathCad.

Выбираем систему уравнений, подставляя значения "а" и "в"

Вбиваем текст в программу MathCad и получаем матрицу.

Находим решение матрицы методом обратной матрицы с помощью функции ISOLVE.

Прямой методом Гаусса с обратным ходом путем проведения ручных расчетов.

Метод приведен в папке «LR2 ручной расчёт» в виде фотографий

Метод Гаусса с обратным ходом в среде MathCad

Для использования метода Гаусса создаем расширенную матрицу, в которую должны войти в качестве составляющих частей матрица коэффициентов и матрица правой части. Для этого используем функциюaugment. Далее расширенную матрицу приводим по методу Гаусса к ступенчатому виду с помощью функции rref, последнийстолбец этой матрицы и является решением. Для его выделения используем функцию submatrix.

Прямой метод Гаусса с обратным ходом в среде MatLab

Составляем m-файл для нахождения решения этой же системы линейных уравнений методом Гаусса в среде MatLab. Для этого в среде MatLab используем функцию rref–с таким же именем, как и в MathCad.

Итерационный метод простой итерации

Преобразовываем систему уравнений таким образом, чтобы из первого уравнения выразить первое неизвестное, из второго – второе неизвестное и т.д. через остальные члены уравнений. Полученные уравнения используем в итерационном процессе вычислений.

Набираем программу для нахождения решения методом просто й итерации.

При выполнении данного пункта заданий определяем решение при изменении точности от 1 до 0,0001.

Результаты расчета	Заданная точность приближения eps
	1,0	0,5	0,1	0,05	0,01	0,005	0,001	0,0005	0.00001
	0,803	0,798	0,794	0,797	0,797	0,797	0,797	0,797	0,797
	1,004	1,001	0,999	1,002	1,002	1,003	1,003	1,003	1,003
	0,129	0,128	0,128	0,129	0,129	0,129	0,129	0,129	0,129
	0,17	0,174	0,177	0,173	0,173	0,173	0,173	0,173	0,173

Итерационный метод Ньютона.

Набираем исходную систему, преобразовываем её в матрицу. Зачем через матрицу Якобиана находим производную. Ищем обратную матрицу. Набираем программу для нахождения значений методом Ньютона.

При выполнении данного пункта определяем решение при изменении точности от 1 до 0,0001.

Результаты расчета	Заданная точность приближения eps
	1,0	0,5	0,1	0,05	0,01	0,005	0,001	0,0005	0.00001
	1,85	1,764	1,737	1,737	1,737	1,737	1,737	1,737	1,737
	2,188	2,145	2,145	2,145	2,145	2,145	2,145	2,145	2,145
	2,058	2,055	2,055	2,055	2,055	2,055	2,055	2,055	2,055

Вывод:

Для решения системы линейных уравнений в численном анализе используют два класса численных методов решения систем линейных уравнений:

1. Прямые методы, которые позволяют найти решение за определенное число операций. К этим методам относятся: метода Гаусса и его модификации (в том числе метод прогонки), метод -разложения и другие.

2. Итерационные методы, основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию. К итерационным методам относятся: метод простых итераций, метод Зейделя и другие

Метод Гаусса:

Достоинство метода – решение находится путем выполнения достаточно малого количества вычислений.

Недостаток – обязательное условие ненулевых ведущих элементов. В противном случае решения не будет, а при значениях этих элементов близких к нулю решение получается со значительными погрешностями.

Метод простой итерации:

Итерационные методы решения являются альтернативой прямым методам Они дают возможность найти приближенное решение с заранее заданной точностью за определенное количество итераций. Количество итераций зависит от вида системы уравнений и соотношения ее коэффициентов. Количество итераций может быть малым, а может быть и бесконечным, т.е. когда система уравнений не решается этим методом.

Метод Ньютона:

Достоинством данного метода является быстрая его сходимость. Недостатком является то, что процесс вычисления матрицы Якоби и нахождение ее обратной матрицы является достаточно трудоемким процессом.

Метод обратной матрицы:

Метод обратной матрицы можно применять при сравнительно небольших размерностях систем линейных уравнений. С увеличением увеличиваются трудности в нахождении обратных матриц.

Предпоследняя цифра зачетной книжки: 5

Последняя цифра зачетной книжки: 3