Численные методы Методические материалы

Продолжая этот процесс, получим матрицу Фробениуса.

P M1 1M21...Mn1 1 A Mn 1 ...M2M1,

если все n 1 промежуточных преобразований возможны. Пример. Привести к виду Фробениуса матрицу:

Решение. Вычисления будем располагать в таблице 4. В строках 1–4 по-

35 a 43

совпасть с элементами строки I , не входящими в контрольный столбец (после замены элемента m33 на -1).

В строках 5–8 в графе M 1 выписываем третью строку матрицы M 1, которая совпадает с четвертой строкой исходной матрицы А. В строках 5–8 в

соответствующих столбцах выписываем элементы матрицы B AM3 , вычисляемые по формулам (2), (2'):

b11 1 2( 1) 1, b21 5 4( 1) 1, b31 7 2( 1) 5, b41 8 8( 1) 0.

51

Преобразованные элементы третьего столбца получаются с помощью ум-

52

Соответственно, последняя строка матрицы В имеет вид (0 0 1 0). Для контроля пополним матрицу В преобразованными по аналогии элементами:

Полученные результаты записываем в столбце Σ/ . Прибавив к ним элементы третьего столбца, будем иметь контрольные суммы:

C31 8( 1) 7 1 8 5 39 .

Те же преобразования проводим над столбцом Σ:

C35 8 3,5 7 6 8 11,5 4 1 166 .

В результате получаем матрицу С, состоящую из строк 5, 6, 7 , 8 с контрольными суммами Σ. Далее, приняв матрицу С за исходную и выделив эле-

мент C32 58,5, продолжим процесс аналогичным образом.

собственные значения исходной матрицы.

6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ. МЕТОД СИМПСОНА (МЕТОД ПАРАБОЛ)

53

поляционный многочлен второй степени L2 x с узлами xi , xi , xi 1 . Нетрудно убедиться, что уравнение этой параболы имеет вид:

Суммируя полученные выражение по i 0,1, 2,..., n 1, получим квад-

ратурную формулу Симпсона (или формулу парабол):

Оценка погрешности. Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой.

Теорема. Пусть функция f имеет на отрезке a, b непрерывную произ-

водную четвертого порядка f 4 x . Тогда для формулы Симпсона справедли-

ва следующая оценка погрешности: I IC M4 b a h4 , где

2880

M4 max f 4 x .

a , b

Замечание. Если число элементарных отрезков, на которые делится отрезок a, b , четно, т.е. n 2m, то параболы можно проводить через узлы с це-

оценки будет справедлива следующая оценка погрешности:

I IC M4 b a h4 . 180

54

Правило Рунге практической оценки погрешности.

Оценка погрешности зависит от длины элементарного отрезка h , и при достаточно малом h справедливо приближенное равенство: I Ih Chk , где Ih приближенное значение интеграла. Если уменьшить шаг h в два раза, то по-

Это приближенное равенство дает оценку погрешности. Вычисление этой оценки называется правилом Рунге. Правило Рунге – это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений, проводимых с разными шагами h . Для формулы Симпсона k 4, и оценка при-

нимает вид: I IC 151 ICh / 2 ICh . Используя правило Рунге, можно построить

процедуру приближенного вычисления интеграла с заданной точностью . Нужно, начав вычисления с некоторого значения шага h , последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значе-

ние Ihi . Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на .

Ih 0,1253 1,5 4 3, 45655 2 1,62818 0,785398.

55

I2h 0, 25 1,5 4 0,941176 0,64 2 0,8 0,785392. 3

I Ic 151 0,785398 0,785392 0,0000006 .

Следовательно, значение интеграла можно счесть Ih 0,785398.

7. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

7.1. ПОСТАНОВКА ЗАДАЧИ КОШИ

Известно, что обыкновенное дифференциальное уравнение первого по-

рядка имеет вид: y t f t, y t .

Решением этого уравнения является дифференцируемая функция y t ,

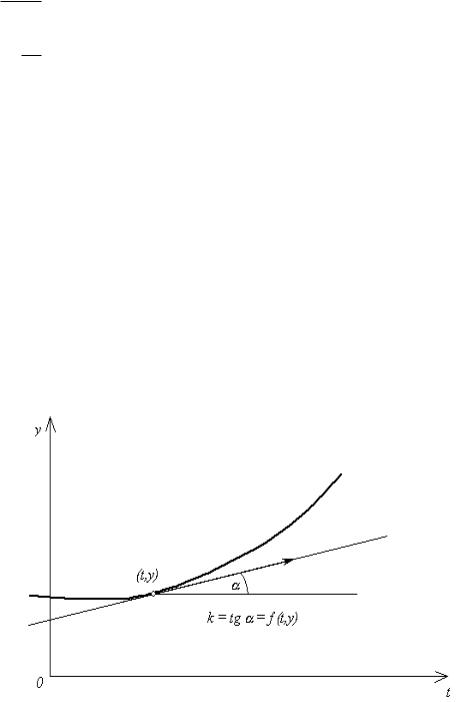
которая при подстановке в уравнение обращает его в тождество. На рис. 13 приведен график решения исходного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.

Рис. 13

Производную y t в каждой точке t, y можно геометрически интернаклона касательной к графику решения, про-

ходящего через эту точку, т е.: k tg f t, y .

Исходное уравнение определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: y t0 y0 , где t0 – некоторое заданное значение аргумента t , а y0 – начальное значение функции.

56

Задача Коши заключается в отыскании функции y y t , удовлетво-

ряющей исходному уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значе-

ния t0 , т. е. для t t0 , T . Разрешимость задачи Коши определяет следующая

Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить при-

ближенные значения искомого решения y t на некоторой выбранной сетке значений аргумента ti , i 0,1,... . Точки ti называются узлами сетки, а ве-

личина hi ti 1 ti – шагом сетки. Часто рассматривают равномерные сетки,

для которых шаг hi постоянен, hi h T t0 . При этом решение получается n

в виде таблицы, в которой каждому узлу сетки ti соответствуют приближенные значения функции y t в узлах сетки yi y ti .

Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений.

Сходимость численных методов решения задачи Коши. Пусть y t –

решение задачи Коши. Назовем погрешностью численного метода функциюi y ti yi , заданную в узлах сетки ti . В качестве абсолютной погрешности

примем величину R max y ti yi .

0 i n

Численный метод решения задачи Коши называется сходящимся, если для него R 0 при h 0. Говорят, что метод имеет p -ый порядок точности, ес-

ли для погрешности справедлива оценка R Chp , p 0, C – константа,

C 0.

57

7.2. МЕТОД ЭЙЛЕРА

Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши

Эти формулы и начальное условие являются расчетными формулами ме-

тода Эйлера.

Тогда для метода Эйлера справедлива следующая оценка погрешности:

видим, что метод Эйлера имеет первый порядок точности.

Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции f t, y t . Грубую оценку по-

грешности дает правило Рунге (правило двойного пересчета), которое ис-

пользуется для различных одношаговых методов, имеющих p -ый порядок точности. Правило Рунге заключается в следующем. Пусть yih / 2 – приближения,

58

Таким образом, чтобы оценить погрешность одношагового метода с шагом h / 2 , нужно найти то же решение с шагом h и вычислить величину, стоящую

Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью . Для этого нужно, начав вычисления с некоторого значения шага h , последовательно уменьшать

это значение в два раза, каждый раз вычисляя приближенное значение yih / 2 , i = 0, 1,..., n . Вычисления прекращаются тогда, когда будет выполнено усло-

i = 0, 1,..., n .

Решение представим в виде таблицы 5:

59

Исходное уравнение есть уравнение Бернулли. Его решение можно найти в явном виде: y 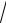2t 1 .

Для сравнения точного и приближенного решений представим точное решение в виде таблицы 6:

Из таблицы видно, что погрешность составляет

R max y ti yi 0,0917 .

0 k 5

7.3. МОДИФИЦИРОВАННЫЕ МЕТОДЫ ЭЙЛЕРА

Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функ-

Эти формулы являются расчетными формулами первого модифициро-

ванного метода Эйлера.

Первый модифицированный метод Эйлера является одношаговым методом со вторым порядком точности.

Второй модифицированный метод Эйлера – Коши. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения

yi 1 yi hf ti , yi .

Затем приближения искомого решения находятся по формуле:

Эти формулы являются расчетными формулами второго модифициро-

ванного метода Эйлера – Коши.

60