
Tipovye_kontrolnye_zadania_s_otvetami_mat
.pdf
в. . Найти область сходимости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
степенного ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 3n 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a n |
|
|
|
|
|
|
|
3n |
|
|
|
|
|
|
|
|
|
|
|
; a n 1 |
|
|
|
|
|
|
|
3n 1 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2n 3n |
1 |
|
|
|
2n 1 3n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
2n 1 |
3n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
R lim |
|
|
a |
n |
|
|
|
|
|
lim |
|
|
|
|
|
2 |
|
|
lim |
|
|
|
|
|
3n 2 |
|
|
|
2 |
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
a n 1 |
|
|
|
|
2n 3n 1 |
3n 1 |
|
|
3 |
|
|
|
|
3n 1 |
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
При x |
|
|
|
получим: |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
1 |
|
|
|
|
. Так как |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 2n 3n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
3n |
1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
и ряд |
1 |
расходится, то, согласно признаку |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3n 1 |
|
|
3n |
|
|
|
|
|
|
|
|
|
3 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
сравнения, будет расходиться и ряд |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
При x |
|
|
|
|
|
получим: |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
xn |
|
|
|
1 |
|
. Так как |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
2n 3n 1 |
|
|
|
3n 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 и |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
, то из выполнения обоих |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
n |
|
|
3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n 1 |
|
|
3 n 1 1 |
|
|
|
|
|
|
|
3n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
условий признака Лейбница для ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и расходимости ряда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3n |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
, следует, что ряд |
|
|
|
|
|
|
|
сходится условно. Окончательно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3n 1 |
|
|
|
3n 1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
получаем такой интервал сходимости: |
|
|
|
|
|
|
|
2 |
x |
|
2 |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г. Решить дифференциальное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

dy 
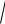 y dx x
y dx x
dyy dxx
dyy dxx
y 12 dy dxx
y 12 ln x const
12
2
 y ln x const
y ln x const
д.Найти решение задачи Коши |
y y e2x y2 |
; y 0 1. |
|
|
|
|
|
|
Постановка задачи и план решения: Линейные уравнения первого
порядка.
Решить задачу Коши для уравнения y'+f(x)y=g(x) (1)
с начальным условием y(x0)=y0. (2)
План решения.
Способ 1.
1. Ищем решение уравнения (1) в виде
, (3)
где u и v – неизвестные функции 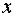 .
.
2. Уравнение (1) принимает вид
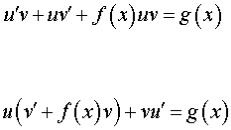
. (4)
3. Преобразуем уравнение (4) к виду
(5)
и полагаем 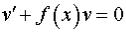 . Это не сужает множество решений y, т.к. уравнение (5) содержит две неизвестные функции.
. Это не сужает множество решений y, т.к. уравнение (5) содержит две неизвестные функции.
4. Решаем уравнение с разделяющимися переменными 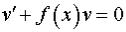 .
.
Найдя 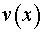 , подставляем его в уравнение (5) и находим
, подставляем его в уравнение (5) и находим 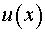 .
.
5.Записываем общее решение уравнения (1) в виде 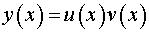 .
.
6.Используя начальные условия (2), получаем решение поставленной задачи Коши.
Способ 2.
1. Записываем соответствующее однородное линейное уравнение:
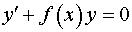 . (6)
. (6)
Это уравнение с разделяющимися переменными.
2. Разделяя переменные и интегрируя, получим общее решение однородного уравнения (6)
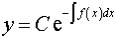 . (7)
. (7)
3. Применяем метод вариации произвольной постоянной.
а) ищем решение неоднородного уравнения (1) в виде (7), считая 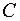 неизвестной функцией от x, т.е. полагая C=C(x);
неизвестной функцией от x, т.е. полагая C=C(x);
б) подставляем в уравнение (1) y и 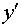 , определяемые из соотношения (7), где C=C(x). Из полученного дифференциального уравнения определяем функцию C(x).
, определяемые из соотношения (7), где C=C(x). Из полученного дифференциального уравнения определяем функцию C(x).
4. Общее решение неоднородного уравнения получаем в виде

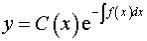 (7а)
(7а)
Здесь C(x) содержит произвольную постоянную 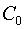 .
.
5. Использую начальные условия (2), находим значение и получаем решение поставленной задачи Коши.
Замечание. Иногда бывает удобным представить x как функцию от y,
т.е.x=x(y).
д.Найти решение задачи Коши |
y y e2x y2 |
; y 0 1. |
|
|
|
|
|
|
Способ 1. |
|
|
Полагаем |
. Тогда |
|
|
. |
|
|
|
|
|
|||||||||||
u v uv uv e2x u2 v2 ; |
|
|
|
|
|
|
|
|
|
|
||||||||||
u v u v v e2x u2 v2 ; |
|
|
|
|
|
|
|
|
|
|
||||||||||
v v 0; |
dv |
dx; ln v x; |
v e x . |
|
|
|
|
|||||||||||||
v |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем u e x e2x u2e 2x u2 ; |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
du |
ex dx; |
|
du |
ex dx; |
1 |
ex C; u |
|
1 |
; |
||||||||||
2 |
2 |
|
u |
e |
x |
|||||||||||||||
|
u |
|
u |
|
|
|
|
|
|
C |
|
|||||||||
y |
|
e x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ex C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Учитывая y 0 1, получим: 1 |
|
e0 |
1 |
|
|
|
|
|
||||||||||||
|
|
|
; 1 |
|
|
; C |
0. |
|
||||||||||||
e0 |
C |
C 1 |
|
|||||||||||||||||
Следовательно, y e 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: y e 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
е.Найти решение ДУ |
|
|
|
|
|
y 7 y 6y sin x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
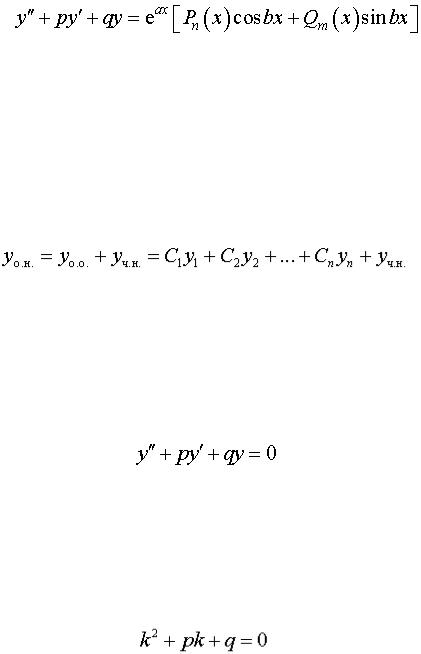
Постановка задачи и план решения: Линейные уравнения с
постоянными коэффициентами
Постановка задачи. Найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами
,
где 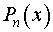 – многочлен степени
– многочлен степени 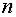 ,
, 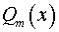 – многочлен степени
– многочлен степени 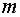 ;
; 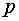 ,
, 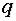 ,
, 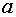 ,
, 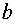 – действительные числа.
– действительные числа.
План решения.
Общее решение неоднородного линейного уравнения 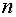 -го порядка имеет следующую структуру:
-го порядка имеет следующую структуру:
, (1)
где 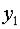 ,
, 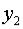 , …,
, …, 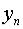 – фундаментальная система решений,
– фундаментальная система решений, 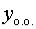 – общее
– общее
решение соответствующего однородного уравнения, 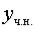 – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
1. Записываем соответствующее однородное уравнение
(2)
и ищем его решение в виде 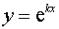 , где k – неизвестное число.
, где k – неизвестное число.
Подставляя 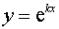 ,
, 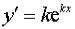 и
и 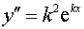 в уравнение (2) и сокращая
в уравнение (2) и сокращая 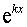 , получаем так называемое характеристическое уравнение
, получаем так называемое характеристическое уравнение
. (3)
2. Решаем характеристическое уравнение. Обозначим корни
характеристического уравнения 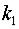 и
и 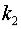 . Тогда фундаментальная система решений и общее решение уравнения (2) записываются в одном из следующих трех видов:
. Тогда фундаментальная система решений и общее решение уравнения (2) записываются в одном из следующих трех видов:
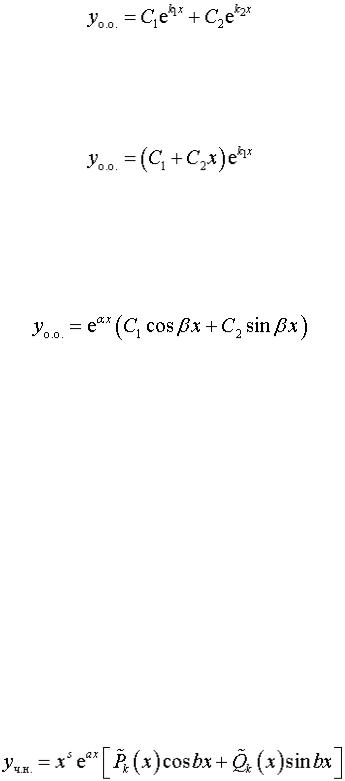
а) если 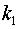 и
и 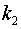 вещественны и
вещественны и  , то фундаментальная система решений – это
, то фундаментальная система решений – это 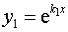 ,
, 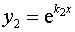 и общее решение имеет вид
и общее решение имеет вид
;
б) если 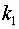 и
и 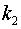 вещественны и
вещественны и 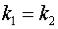 , то фундаментальная система решений – это
, то фундаментальная система решений – это 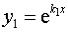 ,
, 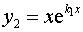 и общее решение имеет вид
и общее решение имеет вид
;
в) если 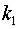 и
и 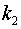 комплексные, т.е.
комплексные, т.е. 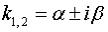 , то фундаментальная
, то фундаментальная
система решений – это 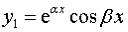 ,
, 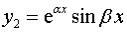 и общее решение имеет вид
и общее решение имеет вид
.
3. Ищем какое-либо частное решение неоднородного уравнения. Поскольку правая часть уравнения имеет вид
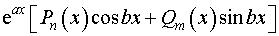 , (4)
, (4)
то можно применить метод подбора частных решений.
Если a ib не является корнем характеристического уравнения (3), то
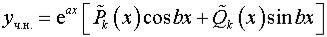 ,
,
где  и
и 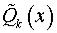 – многочлены степени
– многочлены степени 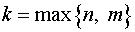 с неопределенными коэффициентами.
с неопределенными коэффициентами.
Если a ib есть корень характеристического уравнения (3) кратности 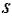 , то
, то
где 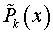 и
и 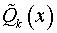 – многочлены степени
– многочлены степени 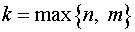 с неопределенными коэффициентами.
с неопределенными коэффициентами.

4. Находим неопределенные коэффициенты, подставив 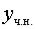 в исходное уравнение. Записываем ответ в виде (1).
в исходное уравнение. Записываем ответ в виде (1).
Замечание. Аналогично решаются линейные дифференциальные уравнения с постоянными коэффициентами любого порядка.
е.Найти решение ДУ |
y 7 y 6y sin x |
|
Решение уравнения будем искать в виде y = erx. Для этого составляем
характеристическое уравнение линейного однородного
дифференциального уравнения с постоянными коэффициентами: r2 -7 r + 6 = 0
D = (-7)2 - 4 • 1 • 6 = 25
Ошибка! Ошибка!
Корни характеристического уравнения:
r1 = 1 r2 = 6
Следовательно, фундаментальную систему решений составляют функции:
y1 = ex y2 = e6x
Общее решение однородного уравнения имеет вид: y = C1ex + C2e6x
Рассмотрим правую часть: f(x) = sin(x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) - некоторые полиномы имеет частное решение
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 1, α = 0, β = 1.
Следовательно, число α + βi = 0 + i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y* = Acos(x) + Bsin(x)
Вычисляем производные: y' = B•cos(x)-A•sin(x)
y'' = -A•cos(x)-B•sin(x)
которые подставляем в исходное дифференциальное уравнение:

y'' -7y' + 6y = (-A•cos(x)-B•sin(x)) -7(B•cos(x)-A•sin(x)) + 6(Acos(x) + Bsin(x))
= sin(x)
или
7•A•sin(x)+5•A•cos(x)+5•B•sin(x)-7•B•cos(x) = sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
7A + 5B = 1
5A -7B = 0
Решая ее, находим:
A = 7/74;B = 5/74;
Частное решение имеет вид:
y* = 7/74cos(x) + 5/74sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид: y = y + y* = C1ex + C2e6x + 7/74cos(x) + 5/74sin(x)
Контрольная работа по теме «Основные законы теории вероятностей».
Примерные задания на контрольную работу:
Задача 1.
Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению и 20 задач по интегральному исчислению. Для сдачи зачета студент должен решить первый же доставшийся наугад билет из трех задач по одной задаче на каждую тему. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение. Число билетов, которое может составить преподаватель, равно
N 10 20 20 4000 .
Число билетов, которое знает студент равно
K 51815 1350.
Считая, что студенту билет достается случайным образом и что это равновероятные события, получаем вероятность сдачи зачета:
P |
1350 |
|
135 |
|
27 |
0,3375. |
|
4000 |
400 |
80 |
|||||
|
|
|
|
Задача 2.
Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению, 20 по интегральному

исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
Решение № 1. Студент знает 38 задач из пятидесяти, поэтому вероятность
сдать зачет равна P( A) |
38 |
0,76. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение № 2. Вероятность получить задачу по пределам (событие H1 ) равна |
||||||||||||||||||||
P(H ) |
10 |
|
0,2 , |
вероятность |
получить задачу |
по |
дифференциальному |
|||||||||||||
|
|
|||||||||||||||||||
1 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
исчислению (событие |
|
H |
|
) |
равна |
P(H |
|
) |
20 |
|
0,4 |
=0,4, |
вероятность |
|||||||
|
2 |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получить |
задачу |
по |
интегральному |
исчислению (событие |
H3 ) равна |
|||||||||||||||
P(H |
|
) |
20 |
0,4 . Если событие A означает, что задача решена, то условные |
||||||||||||||||
3 |
|
|||||||||||||||||||
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вероятности решить задачу при условии, что это задача по пределам, дифференциальному или интегральному исчислению, соответственно равны:
P(A |
|
H ) |
5 |
0,5 |
; P( A |
|
H |
) |
18 |
0,9 |
; P( A |
|
H |
) |
15 |
0,75 . |
|
|
|
||||||||||||||
|
|
1 |
10 |
|
|
|
2 |
|
20 |
|
|
|
3 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
События H1 , H 2 и |
H3 попарно несовместны и одно из них всегда наблю- |
|||||||||||||||
даемо при любом исходе. Тогда по формуле полной вероятности
Р А Р A H1 P H1 Р A H2 P H2 Р A H3 P H3
находим вероятность сдачи зачета
Р А 0,5 0,2 0,9 0,4 0,75 0,4 0,1 0,36 0,3 0,76 .
Задача 3.
В студенческой группе 25 человек, из них 15 студентов и 10 студенток. Наугад выбирается делегация на студенческую конференцию в составе четырѐх человек. Какова вероятность, что изберут двух студентов и двух студенток?
Решение. Число способов выбрать четырѐх человек в делегацию из 25 человек в группе равно числу сочетаний четырѐх предметов из 25:
N C4 |
|
25! |
|
|
25 24 23 22 |
25 23 22 575 22 12650 . |
|
|
|||||
25 |
|
4! 21! |
|
1 2 3 4 |
||
|
|
|
||||
Аналогично находим число способов выбрать в делегацию двух студентов из
15:

N C2 |
|
15! |
|
|
|
15 14 |
15 7 105 |
|||||||
|
|
|
|
|
||||||||||
1 |
|
15 |
|
2! 13! |
|
1 2 |
||||||||
|
|
|
|
|
||||||||||
и двух студенток из 10: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
C2 |
|
10! |
|
|
10 9 |
45. |
|||||
|
2 |
|
|
|||||||||||
|
|
10 |
|
2! 8! |
|
1 2 |
||||||||
|
|
|
|
|
|
|
||||||||
Следовательно, число способов выбрать делегацию из четырѐх человек, в составе которой две студентки и два студента равно
ND N1N2 105 45 4725 .
Считая, что исходы выборов равновероятны, получаем вероятность такого выбора:
P |
|
4725 |
|
189 |
0,374. |
||
|
|
|
|
||||
12650 |
506 |
||||||
|
|
|
|||||
Задача 4.
В автоколонне 10 автобусов. Вероятность того, что у автобуса на линии не будет поломок в течение одной смены, равна p 0,8 . Какова вероятность
того, что в течение смены поломок не будет не менее чем у девяти автобусов?
Решение. Вероятность того, что у k автобусов не будет поломок в течение смены, определяется формулой Бернулли:
pk Cnk pk (1 p)n k .
Тогда искомая вероятность равна p9 p10 или
p9 p10 C109 0,890,21 C1010 0,8100,20 1,8 0,89 0,810 2,6 0,810 0,2792 .
Задача 5.
Вероятность изготовления на станке нестандартного изделия равна q 0,05 .
Какова вероятность обнаружить в партии из 1000 изделий, изготовленных на таком станке, от 940 до 960 стандартных изделий?
Решение. Пусть случайная величина X есть число стандартных деталей, обнаруженных в партии. При большом числе изделий в партии (n 1000) и
вероятности изготовления стандартной детали p 0,95 близкой к единице,
можно использовать интегральную формулу Муавра – Лапласа для определения вероятности того, что число стандартных изделий окажется между k1 940 и k2 960 :
|
|
k |
2 |
np |
k |
np |
||||||
P(k X k |
) |
|
|
|
|
|
1 |
|
|
, |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|||||||||
1 |
2 |
|
|
npq |
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
