
Высшая математика
.docx1. Числовые ряды. Основные определения, свойства. Ряд геометрической прогрессии.
Определение:
Пусть задана бесконечная числовая
последовательность![]()
Числовым рядом называется бесконечная сумма
![]()
Числа ![]() называются,
соответственно, первым, вторым, n–м
… членами ряда.
называются,
соответственно, первым, вторым, n–м
… членами ряда. ![]() называется
также общим членом ряда. Ряд считается
заданным, если известен общий член
ряда
называется
также общим членом ряда. Ряд считается
заданным, если известен общий член
ряда ![]() как
функция его номера n:
как
функция его номера n: ![]() .
.
Определение:
Сумма n первых
членов ряда называется n–й
частичной суммой ряда: ![]() .
.
Определение:
Если существует конечный предел ![]() ,
то его называют суммой ряда, а ряд при
этом называется сходящимся. Если
,
то его называют суммой ряда, а ряд при
этом называется сходящимся. Если ![]() не
существует или равен бесконечности, то
ряд называется расходящимся.
не
существует или равен бесконечности, то
ряд называется расходящимся.
В
школьном курсе математики рассматриваются
такие ряды, как натуральный ряд чисел
и бесконечная геометрическая прогрессия: ![]() .
Известно, что при
.
Известно, что при ![]() сумма
бесконечно убывающей геометрической
прогрессии равна
сумма
бесконечно убывающей геометрической
прогрессии равна ![]() ,
то есть бесконечно убывающая геометрическая
прогрессия является сходящимся числовым
рядом.
,
то есть бесконечно убывающая геометрическая
прогрессия является сходящимся числовым
рядом.
Простейшие свойства числовых рядов
|
Простейшие свойства числовых рядов |
||||
|
Теорема
1: Если ряд
сходится и имеет сумму S, то ряд
где λ–произвольное число, также сходится и имеет сумму λ·S |
Теорема
2: Если ряды![]() (1)
(1)![]() (3)
(3)
|
|
|
|
сходятся
и имеют суммы S и ![]() соответственно,
то ряды
соответственно,
то ряды![]() (4)
(4)
|
|
называемые
суммой и разностью соответственно рядов
(1) и (3), также сходятся и имеют
суммы ![]() соответственно.
соответственно.
Теорема
3: Ряды сходятся или сходятся одновременно![]() (1)
(1)
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Теорема 4: (необходимый признак сходимости ряда).
Если
ряд
сходится,
то Следствие: (Достаточный признак расходимости числового ряда.)
Если
у числового ряда
2. Необходимый признак сходимости числового ряда. Примеры.
Теорема.
Если ряд сходится, то Доказательство. Пусть ряд u1+u2+…+un…
сходится,
то есть существует конечный предел
Тогда
имеет место также равенство
так
как при n
из
первого равенства
второе, получаем
Следствие. Если Пример.
Ряд
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того,
что Позже докажем, что так называемый гармонический ряд
расходится,
хотя
3. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения. Признаки сравнения рядов
Даны
два ряда
Если
Если Пример Исследовать на сходимость ряд
Рассмотрим
расходящийся ряд
Он
расходится, так как получен из
гармонического ряда отбрасыванием u1=1.
Так как ln(n+1)<n+1 при
любом n=1,2,…,
то Предельные признаки сравнения рядов
Пусть
даны два ряда
Так
называемый обобщенный
гармонический ряд
4. Достаточные признаки сходимости знакоположительных рядов: признак Даламбера, радикальный признак Коши. Признак Даламбера
Пусть
Если
Если
Если
Пример:
Исследовать на сходимость ряд Применим признак Даламбера
следовательно, ряд сходится. Радикальный признак Коши
Снова
рассмотрим ряд
Если
Если
Если
5. Достаточный признак сходимости знакоположительных рядов: интегральный признак Коши. Обобщённый гармонический ряд. Пусть
имеем знакоположительный ряд
Пусть
далее, на промежутке 1) 2) f (x) непрерывна, 3) f (x) монотонно убывает, 4) f (n) = an, для целочисленных значений аргумента х = n = 1, 2, 3, … Тогда:
· если
несобственный интеграл
· если
несобственный интеграл
Гармонический
ряд - числовой ряд
Каждый
член такого ряда, начиная со второго,
является гармоническим
средним двух
соседних - этим объясняется название.
Отдельные члены ряда стремятся к нулю,
но его сумма расходится, что было
доказано Н. Оремом (ок. 1350),
П. Менголи (1650), братьями И. и
Я. Бернулли в конце 17 в. и
Г. Лейбницем (1673):
Л. Эйлером (1740) было получено асимптотическое выражение для суммы первых n членов ряда: sn = ln(n) + C + εn, где C = 0,5772156649... - постоянная Эйлера, а εn → 0 при n → ∞.
Обобщённый
гармонический ряд
6. Знакочередующиеся ряды. Признак Лейбница. Определение: Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными числовыми рядами, так как они получаются умножением знакоположительных числовых рядов на (–1). Изучение знакопеременных рядов начнем с частного случая–знакочередующихся рядов.
Определение:
Числовой ряд вида Теорема: (признак Лейбница) Если для знакочередующегося числового ряда
выполняются два условия:
Члены
ряда убывают по модулю
Доказательство: Рассмотрим частичную сумму четного числа членов ряда
По условию U1>U2>…>U2n–1>U2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n иS2n > 0 при любом n. С другой стороны S2n=U1–[(U2–U3)+(U4–U5)+…+(U2n–2–U2n–1)+U2n] Выражение в квадратных скобках положительно и S2n>0, поэтому,
S2n<U1 для
любого n.
Таким образом, последовательность
частичных сумм S2n возрастает
и ограничена, следовательно, существует
конечный Рассмотрим теперь частичную сумму нечетного числа членов ряда S2n+1=S2n+U2n+1. Перейдём в последнем равенстве к пределу при n®¥:
Таким
образом, частичные суммы как четного,
так и нечетного числа членов ряда
имеют один и тот же предел S,
поэтому Пример: Исследовать на сходимость ряд.
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
7. Общий достаточный признак сходимости знакопеременного ряда. Абсолютная и условная сходимости. Примеры. Теорема: (Достаточный признак сходимости знакопеременного ряда) Пусть
знакопеременный ряд. Пусть сходится ряд, составленный из абсолютных величин его членов
Тогда ряд (2) тоже сходится. Доказательство: Рассмотрим вспомогательный ряд
Очевидно
0£Un+|Un|£2|Un|
при всех n=1,2,3….
Ряд (3) сходится по условию, поэтому
сходится ряд Замечание:
Обратное
утверждение неверно. Если данный ряд
сходится, то ряд, составленный из
абсолютных величин его членов, может
и расходится. Например, ряд
Ряд Пример 1.
Исследовать
на сходимость ряд Решение. Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем
поскольку Пример 2.
Исследовать
на сходимость ряд Решение. Попробуем применить признак Лейбница:
Видно, что модуль общего члена не стремится к нулю при n → ∞. Поэтому данный ряд расходится.
8. Функциональные ряды. Область сходимости.
Функциональный
ряд, его сходимость.
Рассмотрим ряд,
ПРИМЕР 1. Нахождение области сходимости функционального ряда.
Равномерная
сходимость функционального ряда.
Пусть
ПРИМЕР 2. Изучение сходимости функционального ряда.
Исследование
на равномерную сходимость.
Признак Вейерштрасса равномерной
сходимости функционального ряда: если
существует сходящийся числовой
ряд
9. Степенные ряды. Теорема Абеля. Определение 1.1. Степенным рядом называется функциональный ряд вида
Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида
Такой ряд всегда сходится при x=0 и, значит, его область сходимости есть непустое множество.
Теорема
1.1. (теорема Абеля). Если
степенной ряд (1.2) сходится при
некотором Доказательство. Пусть числовой ряд
сходится.
Поэтому
Рассмотрим
теперь ряд
Предположим
теперь, что ряд (1.3) расходится, а
ряд (1.2) сходится при Теорема Абеля позволяет дать описание области сходимости степенного ряда.
10. Интервал и радиус сходимости степенного ряда. Интервал и радиус сходимости Рассмотрим
функцию
или
на основе признака Даламбера:
Пример 1. Найти
радиус и интервал сходимости степенного
ряда Решение. Сделаем
замену: u
= x + 3.
Тогда ряд принимает вид
Соответственно, интервал сходимости равен (− ∞; ∞).
11. Ряды Тейлора и Маклорена. Достаточное условие разложимости функции в рял Тейлора. Имеем степенной ряд, сходящийся на интервале (x0 – R, x0 + R). Суммой ряда является функция f(x)
Покажем, что коэффициенты этого ряда связаны простым соотношением с f(x) .
Будем последовательно дифференцировать обе части равенства ( 11 ) и вычислять производные при х = х0
f (x) = a0 + a1(x – x0) + a2(x – x0)2 + a3(x – x0)3 + … + an(x – x0)n + . . . , f(x0) = a 0
f ‘(x) = a1 + a2(x – x0) + a3(x – x0)2 + … + n an(x – x0)n-1 + . . . , f ‘(x0) = a1
f ‘’(x) = a2 + a3(x – x0) + a4(x – x0)2 + … + n(n – 1) an(x – x0)n-2 + . . . , f ‘)’(x0) = 2 a2
f ‘’’(x) = a3 + a4(x – x0) + a5(x – x0)2 +…+ n(n–1)(n–2)an(x – x0)n-3 + . . . , f’’’(x0) = 23 a3
f(n) (x) = n(n–1)(n–2) . . . 2 1 an + . . . , f ( n )(x0) = n ! a n
Отсюда находим коэффициенты a0 = f(x0) , an = f ( n )(x0) / n ! ( 12 )
Таким образом, если бесконечно дифференцируемая в точке х0 функция f(x) разлагается в степенной ряд, то этот ряд имеет вид
f(x)
=
Теорема1(достаточное
условие разложимости функции в
степенной ряд). Пусть
12. Разложение функции y=cosx в ряд Маклорена.
В
соответствии с формулой
Для
ряда характерна абсолютная сходимость
на интервале
13. Разложение функции y=sinx в ряд Маклорена.
Разложение
функции Вычислим производные данной функции.
… … … …
… … … …
Значение
Исследуем
остаточный член ряда.
Рекомендуем
показать самостоятельно, что областью
сходимости ряда является помежуток
14. Разложение функции y=ex в ряд Маклорена.
Разложение
функции
Составим
для функции
Найдем
область сходимости этого ряда
следовательно,
областью сходимости ряда является
промежуток
15. Основные определения (случайное, достоверное, невозможное события, действия над событиями, полная группа событий, совместные и несовместные события) Возможные результаты единичной операции, или испытания S, называются случайными событиями. Случайное событие - это такое событие, которое может произойти, а может и не произойти при испытании S. Вместо "произойти" говорят также "наступить", "появиться", "иметь место". Достоверным называется событие, которое обязательно наступает при проведении данного случайного эксперимента. Например, события
являются, очевидно, достоверными. Невозможным называется событие, которое при проведении данного случайного эксперимента никогда не происходит. Например, события
являются, очевидно, невозможными. 1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.
2. Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.
3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.
4. Событие называется противоположным событию A, если оно удовлетворяет двум свойствам.
Формулы
де Моргана:
5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания. События A и B называются несовместными, если они не имеют общих элементарных событий. C=AxB=V Тут V - пустое множество. Полная группа событий. Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + ... + Р (Аn) = 1.
16. Классическое определение вероятности. Свойства вероятности. Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу
Свойство 1. Вероятность достоверного события равна единице Свойство 2. Вероятность невозможного события равна нулю. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству .
17. Теоремы сложения вероятностей. Следствия. Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Определение. Противоположными называются два несовместных события, образующие полную группу.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
18. Теоремы умножения вероятностей. Следствия. Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РA (В). (*)
З а м е ч ан и е. Применив формулу (*) к событию ВА, получим Р (ВА) = Р (В) РB (А), или, поскольку событие ВА не отличается от события АВ, Р(АВ) = Р (В) РB (А). (**)
Сравнивая формулы (*) и (**), заключаем о справедливости равенства Р (А) РA (В) = Р (В) РB (А). (***) С л е д с т в и е. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
где
является вероятностью события An, вычисленной в предположении, что события А1,А2,..., Аn — 1 наступили. В частности, для трех событий Р (AВС) = Р (А) РA (В) РAB (С).
Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д.
19. Формула полной вероятности. Формула Байеса.
Если
событие А может
произойти только при выполнении одного
из событий
Эта формула называется формулой полной вероятности.
Вновь
рассмотрим полную группу несовместных
событий
Если
событие А произошло,
то это может изменить вероятности
гипотез По теореме умножения вероятностей
откуда
Аналогично, для остальных гипотез
Полученная
формула называется формулой
Байеса (формулой
Бейеса).
Вероятности гипотез
20. Повторение испытаний. Формула Бернулли. Пусть
проводится n независимых
испытаний, в каждом из которых
событие A может
появиться с вероятностью p и
не появиться с вероятностью q
= 1 - p.
Обычно первый из двух возможных исходов
называют удачей,
а второй — неудачей (разумеется,
такое деление условно, и, возможно,
кому-то захочется назвать два возможных
исхода удачей и неудачей противоположным
образом). Поставим задачу выяснить
вероятность того, что за n испытаний
произошло ровно k удач,
неважно, в какой последовательности
(естественно, что всегда
1) Отметим, что при фиксированном n и при малых значениях k вероятность достаточно маленькая, и это обусловлено тем, что маловероятно, что нам не повезет ни разу (не будет ни одного удачного исхода). С ростом k эта вероятность будет расти, при некотором значении достигнет максимума и далее будет убывать, становясь при k близких к n снова достаточно малой. Малое значение вероятности при k, близких к n, обусловлено тем, что маловероятно, что все испытания будут удачные.
21. Локальная и интегральная теоремы Муавра-Лапласа.
Пусть
в каждом из Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то
Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то
P(n;
k1, k2) Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
а)
б)
при больших
Теоремы
Лапласа дают удовлетворительное
приближение при
22. Дискретная случайная величина. Закон распределения. Примеры д.с.в. Величина, которая в результате испытания может принять то или иное значение, заранее неизвестно какое именно, считается случайной. Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью. Сотношение, устанавливающее связь мужду отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины.Если обозначить возможные числовые значения случайной величины Х через х1, х2, ..., хn,..., а через рi = Р(Х = хi) вероятность появления значения хi, то дискретная случайная величинаполностью определяется табл: xi х1 x2 ... xn pi p1 p2 ... pn Таблица называется законом распределения дискретной случайной величины Х.
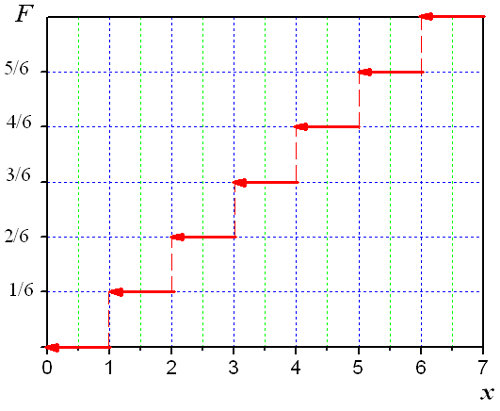
Ряд распределения можно изобразить графически. Получим многоугольник распределения вероятностей(полигон распределения). Дискретная случайная величина может быть задана функцией распределения. Функцией распределения случайной величины Х называется функция F(х), выражающая вероятность того, что Х примет значение, меньшее чем х: F(x) = P(X < x) = е pi, где суммирование по хi < x Функция F(x) есть неубывающая функция. Для дискретных случайных величин функция распределения F(х) есть разрывная ступенчатая функция, непрерывная слева.
Пример Вероятность попадания случайной величины Х в промежуток от a до b выражается формулой Р( <= X < ) =F( ) - F() По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле р = 0,8. Требуется: а)
найти закон
распределения дискретной случайной
величины б)
найти вероятности
событий: Решение. а) Возможные
значения случайной
величины
Закон распределения Проверка: 0,0016 + 0,0256 + 0,1536 + 0,4096 + 0,4096 = 1. б) Вероятность
событий
23. Математическое ожидание дискретной случайной величины. Его свойства. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значенийна их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C. 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X). 3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z). 4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XЧYЧZ) = M(X)ЧM(Y)ЧM(Z). Все эти свойства имеют большое практическое значение.
24. Дисперсия дискретной случайной величины. Её свойства. Среднее квадратическое отклонение. Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2
Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)
Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)
25. Непрерывная случайная величина. Интегральная функция распределения. Свойства. Если X - случайная величина, то функция F(x) - интегральная функция распределения вероятностей, или просто функция распределения (иногда применяют термин кумулятивная функция распределения) случайной величины определяет вероятность P того, что случайная величина принимает значение, меньше x, т.е. F(x) = P( X < x) Функция распределения содержит всю информацию о случайной величине, поэтому изучение случайной величины заключается в исследовании ее функции распределения. Функция распределения полностью характеризует случайную величину и является одной из форм закона распределения. Из определения следует, что функция распределения любой случайной величины обладает следующими свойствами: Свойства F(x): 1. Интегральная функция распределения принимает значения от 0 до 1.
2. F(x)
- неубывающая функция, то есть F(x2) 3. Вероятность того, что случайная величины X примет значение, заключенное в интервале (а, b) равна приращению интегральной функции распределения на этом интервале:
4. Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то:
F(x)
= 0, если x Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Например для функции распределения числа очков выпавших при одно бросании игральной кости.
26. Непрерывная случайная величина. Дифференциальная функция распределения(плотность распределения).
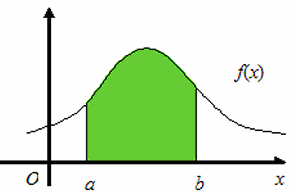
Непрерывную
случайную величину удобнее характеризовать
плотностью распределения (дифференциальной
функцией распределения)
Следовательно,
функция распределения F(x) выражается
через плотность распределения:
Вероятность
того, что непрерывная случайная
величина X примет значение, принадлежащие
интервалу (a, b) равна определенному
интегралу от дифференциальной функции,
взятому в пределах от a до b:
Свойства
1.
2.
27. Равномерное распределение. Пусть производится n независимых испытаний. Случайная дискретная величина X имеет равномерное распределение, если она принимает значения хi
(i= 1, n ) с одинаковыми вероятностями
Случайная непрерывная величина X на промежутке (а,b) имеет равномерное распределение, если плотность распределение
на заданном промежутке, а вне его р(х)=0. Функция распределения в этом случае имеет вид:
Математическое ожидание и дисперсия случайной непрерывной величины X вычисляется следующим образом:
28. Нормальное распределение. Случайная непрерывная величина X имеет нормальное (гауссово) распределение, если ее плотность распределения вероятности имеет вид
где
Если а=0 и σ=1, то нормальное (гауссовое) распределение называется стандартным нормальным (гауссовым) распределением (таблица плотности вероятности нормальной случайной величины), плотность которого равна
а функция распределения (функция Лапласа) (таблица функции Лапласа)
Вероятность попадания в заданный интервал (α;β) нормально распределенной случайной величины с параметрами а, σ вычисляется по формуле:
с использованием интеграла вероятности
Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания а:
,где δ — величина отклонения.
Полагая в этой формуле δ=3σ, получаем P(|X-a|<δ)=2Ф(3)=2*0.49865=0.9973 Этот результат носит название «правило трех сигм». Таким образом, в 99,7% случаях все значения нормального распределения случайной величины сосредоточены в интервале (-3σ+a; 3σ+a). Распределение, заданное на бесконечном интервале, может быть рассмотрено на конечном интервале, и погрешность при такой замене равно ,примерно, 0,3%.
29. Показательное распределение. Функция надёжности. Показательным
(экспоненциальным) называют
распределение верояйюстей, которое
описывается дифференциальной
функцией
Функцией надежности R(f) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t: R(t)=P(T>t) Часто
длительность времени безотказной
работы элемента имеет показательное
распределение, интегральная функция
которого
F(t)=1-e-?t
Следовательно,
в силу соотношения R(t)=P(T>t)=1-F(t)
предыдущего параграфа, функция
надежности, в случае
показательного
распределения
времени безотказной работы элемента,
имеет вид
30. Вариационный ряд. Эмпирическая функция распределения. Полигон. Гистограмма.
Эмпирической
функцией распределения, построенной
по выборке
Иначе
говоря, при любом
Если
элементы выборки
Здесь
Элемент
Эмпирическая
функция распределения имеет скачки
в точках выборки, величина скачка в
точке Можно построить эмпирическую функцию распределения по вариационному ряду:
Другой характеристикой распределения является таблица (для дискретных распределений) или плотность (для абсолютно непрерывных). Эмпирическим, или выборочным аналогом таблицы или плотности является так называемая гистограмма.
Гистограмма
строится по группированным данным.
Предполагаемую область значений
случайной величины
На
каждом из интервалов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
то ряд
,
то ряд  ,
то ряд
,
то ряд  ,
то ряд
,
то ряд 




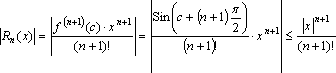 ,
так как
,
так как .Рассмотрим
несколько предельных случаев:
.Рассмотрим
несколько предельных случаев:

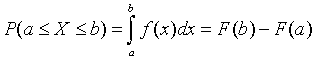
 График
f(x) называют также законом распределения
или кривой распределения.
График
f(x) называют также законом распределения
или кривой распределения.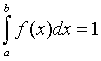 ,
если все возможные значения X принадлежат
интервалу (a, b)
,
если все возможные значения X принадлежат
интервалу (a, b)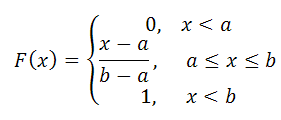




 где ?— положительная
постоянная величина.
Мы
видим, что показательное распределение
определяется одним параметром ?.
Эта особенность показательного
распределения указывает на его
преимущество, по сравнению с
распределениями, зависящими от большего
числа параметров. Обычно параметры
неизвестны и приходится находить
их оценки (приближенные значения);
разумеется, проще оценить один параметр,
чем два, или три и т. д.
Примером
непрерывной случайной величины,
распределенной по показательному
закону, может служить время между
появлениями двух последовательных
событий простейшего потока.
Найдем
интегральную функцию показательного
распределения.
где ?— положительная
постоянная величина.
Мы
видим, что показательное распределение
определяется одним параметром ?.
Эта особенность показательного
распределения указывает на его
преимущество, по сравнению с
распределениями, зависящими от большего
числа параметров. Обычно параметры
неизвестны и приходится находить
их оценки (приближенные значения);
разумеется, проще оценить один параметр,
чем два, или три и т. д.
Примером
непрерывной случайной величины,
распределенной по показательному
закону, может служить время между
появлениями двух последовательных
событий простейшего потока.
Найдем
интегральную функцию показательного
распределения.
 Мы
определили показательное распределение
при помощи дифференциальной функции;
ясно, что его можно определить,
пользуясь интегральной функцией.
Графики
дифференциальной и интегральной
функций изображены на рис. 12.
Мы
определили показательное распределение
при помощи дифференциальной функции;
ясно, что его можно определить,
пользуясь интегральной функцией.
Графики
дифференциальной и интегральной
функций изображены на рис. 12.
 (1)
(1)